Основные понятия о переменном синусоидальном токе

Основные понятия о переменном синусоидальном токе

1.            Основные свойства переменного тока.

2.            Принцип создания синусоидальной ЭДС.

3.            Параметры, характеризующие синусоидальную величину.

4.            Виды сопротивлений в цепи переменного тока: активное, индуктивное, емкостное.

1.     Основные свойства переменного тока

Все наши квартиры освещены с помощью переменного тока. Переменный ток есть не что иное, как вынужденные электромагнитные колебания. Сила тока и напряжение будут меняться с течением времени согласно гармоническому закону.

Изменение напряжения на концах цепи будет вызывать за собой изменение силы тока в цепи колебательного контура. Следует всё же понимать, что изменение электрического поля во всей цепи не происходит мгновенно. Но так как это время, значительно меньше, чем период колебания напряжения на концах цепи, то обычно считают, что электрическое поле в цепи сразу же меняется, как меняется напряжение на концах цепи.Переменное напряжение создается генераторами на электростанциях.

Электрическая энергия почти во всех случаях произ­водится, распределяется и потребляется в виде энергии переменного тока. Это объясняется тем, что переменный ток легко трансформировать (изменять напряжение с по­мощью трансформаторов) и, следовательно, обеспечивать экономичную передачу энергии на большие расстояния. Кроме того, электрическую энергию переменного тока можно легко распределять и преобразовывать в механи­ческую (применение асинхронных электродвигателей) Электромагнитные волны распространяются со скоростью 300 000 км/с. С такой же скоростью распространяется электромагнитная энергия.

Указанными преимуществами переменного тока об­условлено широкое применение его в различных отраслях промышленности и в быту.

Переменный ток впервые был использован русским электротехником П.Н.Яблочковым. В 1876 г. он изобрел аппарат, названный им трансформатором, с помощью ко­торого можно было преобразовывать напряжение пере­менного тока.

Переменным называется ток (напряжение) изменяющий во времени свое направление и величину.

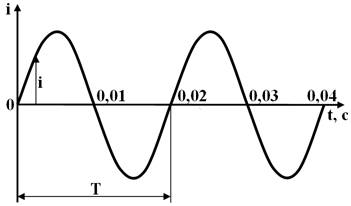
Переменные токи могут быть периодическими и непериодическими. Наибольшее применение находят периодические токи, то есть токи, мгновенные значения которых повторяются через равные промежутки времени, называемые периодом Т (рис. 1).

Промежуток времени, в течение которого ЭДС, на­пряжение или ток проходят полный цикл изменений по величине и направлению, называется периодом перемен­ного тока, а число периодов в секунду  -  частотой пере­менного тока. Частота обозначается буквой  f  и является величиной, обратной периоду:

где Т - период, с.

. 

Рисунок 1. График синусоидального переменного тока

Единицей частоты является герц (Гц), численно рав­ный одному периоду в секунду: 1 Гц = 1/с = с^-1.

Используются также кратные единицы:

· 1 килогерц (кГц) = 1000 Гц = 10³ Гц;

· 1 мегагерц (МГц) =1 000 000 Гц = 10⁶ Гц;

· 1 гигагерц (ГГц) в = 10⁹ Гц.

Частота переменного тока в электрических цепях большинства стран составляет 50 или 60 Гц. Это означает, что направление тока (и напряжения) в каждую секунду меняется 100 и 120 раз.

В РФ для электрических сетей установлена стандартная частота переменного тока, равная 50 Гц, которая называется промышленной частотой, в США и Японии – 60 Гц. Выбор такой частоты объясняется тем, что при частоте, меньшей 40 Гц, возрастают габариты, масса, а значит и стоимость электрических машин и трансформаторов и становится заметным для человеческого глаза мигание света осветительных устройств. При больших частотах возрастают потери мощности в электротехнических установках и падение напряжения в линиях электропередачи. При f = 50 Гц длительность периода Т составляет 0,02 с. В некоторых отраслях техники применяют более высокие частоты, например в проводной связи 300 - 5000 Гц, в электротермии 50 - 10⁷ Гц, в радиотехнике и телевидении 10⁵ - 3 ∙ 10¹⁰ Гц.

2.     Принцип создания синусоидальной ЭДС

По закону электромагнитной индукции мгновенное значение ЭДС, индуктированной в витке (рисунок  2), будет:

где В  -  магнитная индукция однородного магнитного поля, Т;

 l  -  длина активной части витка, м;

v  -  окружная скорость витка, м/с;

α  -  угол между на­правлением магнитных линий и направлением движения проводника.

При равномерном вращении витка с угловой ско­ростью ω угол поворота:

Обозначив:

 Получим:

Переменный угол α = ω ∙ t называется фазой ЭДС.

Если замкнуть цепь витка на внешнее сопротивление, то в цепи будет протекать переменный ток, мгновенное значение которого i = I_м ∙ sin(ω ∙ t).

Если отсчет времени t начинается в момент, когда ЭДС и ток не проходят через нуль, то их мгновенные значения определяются из следующих выражений:

В течение времени Т одного периода фаза ЭДС и тока изменяется на угол 2π, следовательно:

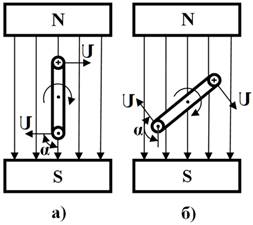
Рисунок 2 - Вращение витка в однородном магнитном поле: а) -  исходное положение (α = 90°); б) -  промежуточное положение (α 90°) 

Откуда:

Величина ω называется угловой частотой (скоростью) переменного тока и измеряется в радианах в секунду (рад/с). Для витка, вращающегося в однородном магнитном поле (рисунок  17), угловая частота равна частоте вращения витка. Так как промышленная частота f = 50 Гц, то угловая частота ω = 2 ∙ π ∙ f = 2 ∙ 3,14 ∙ 50 = 314 рад/с. Если ротор делает n оборотов в минуту, то его угловая частота:

Следовательно, при р парах полюсов генератора между электрической и механической угловой скоростью существует следующая зависимость:

откуда частота:

или

Фазами ЭДС и тока являются аргументы синуса ω ∙ t + ψ_e и ω ∙ t + ψ_i. Величины ψ_e и ψ_i, определяющие значения ЭДС и тока в начальный момент времени (t = 0), называются начальными фазами ЭДС и тока. На рисунке  4.3, а, б, в изображены графики синусоидальных ЭДС, имеющих различные начальные фазы, а на рисунке  4.3, г - графики ЭДС и тока.

Разность фаз ЭДС и тока одинаковой частоты обозначается φ и называется сдвигом по фазе между ЭДС и током:

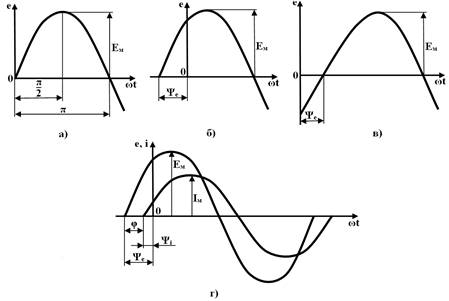
Рисунок 3 - Графики синусоидальных ЭДС:

а) - при Ψ_е = 0; б) - при Ψ_е > 0; в) - при Ψ_е < 0; г) - временные диаграммы е и i со сдвигом по фазе

Если ЭДС и ток имеют одинаковые начальные фазы, то говорят, что они совпадают по фазе. При φ = 180° ток и ЭДС находятся в противофазе. Аналогично этому можно говорить о сдвиге по фазе между двумя ЭДС или двумя токами одинаковой частоты.

3.     Параметры, характеризующие синусоидальную величину.

Сила тока и напряжение переменного тока измеряют­ся соответственно в амперах и вольтах.

Значения переменного тока, напряжения или ЭДС в какой - нибудь момент времени называются мгновенными значениями и обозначаются строчными буквами:

· ток - i,

· напряжение - u,

· ЭДС - е.

Наибольшие мгновенные значения тока, напряжения или ЭДС называются максимальными, или амплитудными. Максимальные значения обозначаются прописными буквами с индексом «м»: ток - I_м, напряжение - U_м, ЭДС - Е_м.

При технических расчетах принято пользоваться не амплитудными, а действующими (эффективными) значениями тока, напряжения и ЭДС. Действующим значением переменного синусоидального тока является такая его величина, которая численно равна величине постоянного тока, протекающего через то же сопротивление и вызывающего выделение такого же количества тепла за один и тот же промежуток времени (за время одного или нескольких периодов Т).

Действующие значения обозначаются прописными буквами:

· ток - I;

· напряжение - U;

· ЭДС - Е.

Между действующим и амплитудным значениями переменного тока существует следующее соотношение:

Для ЭДС и напряжения соотношения аналогичны:

Приборы, предназначенные для измерения напряжения и силы тока, а именно вольтметры и амперметры, показывают действующие значения этих параметров.

Известно, что любая синусоидальная величина характеризуется амплитудой, частотой и начальной фазой.

Значение синусоидальной величины в любой момент времени называют мгновенным. Обозначаются мгновенные значения строчными буквами: напряжение - и, ЭДС - е, ток - i . Зависимости мгновенных значений синусоидальных  напряжения,         ЭДС  и тока         от      времени     определяются выражениями:

e = Em sin(w t + y e ),

i = Im sin(w t + y i ),                                                            

u = Um sin(w t + y u ).

Наибольшее значение синусоидальной величины - амплитуда. Обозначается прописными буквами Е_т, I_m, U_m.

Аргумент синусоидальной величины называется фазой. Например, в выражении

(ωt +ψ _е) – фаза ЭДС.

Значение фазы в начальный момент t = 0 – начальная фаза (ψ_е). На рис. 4 показаны графики синусоидальных ЭДС с разными начальными фазами (отрицательной, положительной, равной нулю).

На графиках начальные фазы показывают стрелками, направленными от начала синусоиды к оси ординат.

Наименьший промежуток времени, по истечении которого мгновенные значения повторяется – период Т. Число периодов в одну секунду - частота f . Единица частоты – герц (Гц). Часто для удобства на графиках горизонтальную ось обозначают не t, a ωt (рис. 4).

Периоду Т соответствует значение аргумента

ωT = 2π. Тогда

f  =  1  = w

T     2p

, а w = 2pf

. При стандартной частоте f = 50 Гц ω =

314 рад/с.

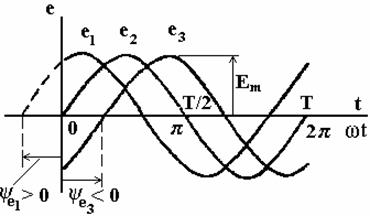
Рис. 4. Графики синусоидальных ЭДС, с разной начальной фазой:

y e1  > 0 , y e2  = 0 , y e3  < 0

Как правило, в силовых цепях синусоидального тока действует один источник электроэнергии. Частота синусоидальной ЭДС этого источника определяет частоту синусоидальных токов и напряжений во всех участках этой цепи. Поэтому частота синусоидальных токов и напряжений во всех участках цепи одна и та же. Следовательно, при анализе соотношений между токами и напряжениями на разных участках цепи этот параметр можно опустить.

Таким образом, при анализе цепей синусоидального тока необходимо характеризовать синусоидальные ток и напряжение двумя обязательными параметрами: величиной (амплитудным значением) и начальной фазой.

Например, в разных участках электрической цепи возникают синусоидальные токи:

i₁ = 2,5 sin(ωt + 15⁰);                                                                                         

i₂ = 2,5 sin(ωt + 50⁰).                                                                                         

Эти токи одинаковы по величине (I_m=2,5А). Однако, эти токи разные, т.к. отличаются начальной фазой и в любой момент времени имеют разные мгновенные значения.

При анализе электрических цепей синусоидального тока важное  значение имеет соотношение по фазе между напряжением и током на заданном участке цепи. Это соотношение характеризуется параметром разность фаз (φ), которая определяется выражением:

j =y u  -y i .                                                                                                   

Разность фаз характеризует угол, на который синусоидальное напряжение опережает по фазе синусоидальный ток.

При φ > 0 напряжение опережает ток по фазе; если φ < 0, то напряжение по фазе отстает от тока; при φ = 0 напряжение и ток совпадают по фазе.

4.                      Виды сопротивлений в цепи переменного тока: активное, индуктивное, емкостное    В состав цепей переменного тока входят резистивные элементы, катушки индуктивности, конденсаторы и элементы, соединенные магнитной или емкостной связью с другими цепями. В резистивных элементах электрическая энергия пре­образуется в другие виды энергии. Резистивный элемент характеризуется значением сопротивления и обладает не­которой индуктивностью и емкостью, влиянием которых в ряде случаев можно пренебречь (например, при низкой частоте). Индуктивный элемент кроме индуктивности обладает также сопротивлением, которым, как правило, пренебречь нельзя. Иногда учитывается и влияние емкости. В емкостном элементе имеются некоторые потери энер­гии, но они относительно невелики, и поэтому их можно не учитывать.   4.1 Цепь с резистивным элементом, имеющим активное сопротивление Активным называется сопротивление про­водника переменному току. Активное сопротивление все­гда больше омического за счет поверхностного эффекта, вытеснения тока к поверхностным слоям проводника. Приемниками электрической энергии, обладающими при промышленных частотах только активным сопротив­лением, являются реостаты, электрические лампы, нагре­вательные приборы, электроплиты и другие устройства, в которых осуществляется преобразование электрической энергии в тепловую. Эту нагрузку мы раньше называли сопротивлением. Теперь будем называть её активным сопротивлением. Сопротивление R называют активным, так как если в цепи будет нагрузка с таким сопротивлением, цепь будет поглощать энергию, поступающую от генератора. Будем считать, что напряжение на зажимах цепи подчиняется гармоническому закону: U = Umcos(ωt). Мгновенное значение силы тока можем вычислить по закону Ома, оно будет пропорционально мгновенному значению напряжения. I = u/R = Umcos(ωt)/R = Imcos(ωt). Сделаем вывод: в проводнике с активным сопротивлением разность фаз между колебаниями напряжения и силы тока отсутствует. Действующее значение силы тока Амплитуда силы тока определяется по следующей формуле: Im = Um/R. Среднее значение квадрата силы тока за период вычисляется по следующей формуле: i2 = (Im)2/2. Здесь Im есть амплитуда колебания силы тока. Если мы теперь вычислим квадратный корень из среднего значения квадрата силы тока, то получим величину, которая называется действующим значением силы переменного тока.  Для обозначения действующего значения силы тока используется буква I. То есть в виде формулы это будет выглядеть следующим образом: I = √(i2) = Im/√2. Действующее значение силы переменного тока будет равно силе такого постоянного тока, при котором за одинаковый промежуток времени в рассматриваемом проводнике будет выделяться столько же теплоты, сколько и при переменном токе. Для определения действующего значения напряжения используется следующая формула. U = √(u2) = Um/√2. Теперь подставим действующие значения силы тока и напряжения, в выражение Im = Um/R.  Получим: I = U/R. Данное выражение является законом Ома для участка цепи с резистором, по которому течет переменный ток. Как и в случае механических колебаний, в переменном токе нас мало будут интересовать значения силы тока, напряжении в какой-то отдельный момент времени. Гораздо важнее будет знать общие характеристики колебаний - такие, как амплитуда, частота, период, действующие значения силы тока и напряжения.  Кстати, стоит отметить, что вольтметры и амперметры, предназначенные для переменного тока, регистрируют именно действующие значения напряжения и силы тока. Еще одним преимуществом действующих значений перед мгновенными является то, что их можно сразу использовать для вычисления значения средней мощности P переменного тока. Для вычисления средней мощности используется следующая формула: P = I2R = UI. Отметим, что измерительные приборы (амперметры и вольтметры переменного тока) регистрируют именно действующие значения. Кроме того, номинальные значения напряжений и токов бытовых приборов также указываются как действующие значения. Так стандартное напряжение в цепи − 220 вольт есть действующее значение, а амплитудное значение этого напряжения равно   4.2 Конденсатор в цепи переменного тока   При изучении постоянного тока мы узнали, что он не может проходить в цепи, в которой есть конденсатор. Так как конденсатор - это две пластины, разделенные слоем диэлектрика. Для цепи постоянного тока конденсатор будет, как разрыв в цепи. Если конденсатор пропускает постоянный ток, значит, он неисправен.   В отличии от постоянного переменный ток может идти и через цепь, в которой присутствует конденсатор. Рассмотрим, как будет меняться сила тока в цепи, содержащей конденсатор, с течением времени. При этом будем пренебрегать сопротивлением соединяющих проводов и обкладок конденсатора. рисунок Напряжение на конденсаторе будет равняться напряжению на концах цепи. Значит, мы можем приравнять эти две величины. u = φ1-φ2 = q/C,   u = Umcos(ωt). Имеем: q/C = Umcos(ωt). Выражаем заряд: q = CUmcos(ωt). Видим, что заряд будет изменяться по гармоническому закону. Сила тока - это скорость изменения заряда. Значит, если возьмем производную от заряда, получим выражение для силы тока. I = q’ = UmCωcos(ωt+π/2). Разность фаз между колебаниями силы тока и заряда, а также напряжения, получилась равной π/2. Получается, что колебания силы тока опережают по фазе колебания напряжения на π/2. Это представлено на рисунке. Из уравнения колебаний силы тока получаем выражение для амплитуды силы тока: Im = UmCω. Введем следующее обозначение: Xc = 1/(Cω). Запишем следующее выражение закона Ома, используя Xc и действующие значения силы тока и напряжения: I = U/Xc. Xc - величина, называемая емкостным сопротивлением. 4.3 Катушка индуктивности в цепи переменного тока Индуктивность в цепи переменного тока будет влиять на силу переменного тока.   Рассмотрим цепь, в которой есть только катушка индуктивности. При этом значение сопротивления катушки и соединительных проводов пренебрежимо мало.  Выясним, как будут связаны напряжение на катушке с ЭДС самоиндукции в ней. При сопротивлении катушки равном нулю, напряженность электрического поля внутри проводника тоже будет равна нулю. Равенство нулю напряженности возможно. Напряженности электрического поля создаваемого зарядами Eк будет соответствовать такая же по модулю и противоположно направленная напряженность вихревого электрического поля, которое появится вследствие изменения магнитного поля. Следовательно, ЭДС самоиндукции ei будет равна по модулю и противоположна по знаку удельной работе кулоновского поля. Следовательно:  ei = -u. Сила тока будет изменяться по гармоническому закону: I = Im sin(ωt). ЭДС самоиндукции будет равна:  Ei = -Li’ = -Lω Im cos(ωt). Следовательно, напряжение будет равно:  U = Lω Im cos(ωt) = Lω Im sin(ωt+ π/2). Отсюда значение действующего напряжения будет равняться Um = Lω Im. Видим, что между колебаниями тока и напряжения получилась разность фаз равная π/2. Следовательно, колебания силы тока отстают от колебания напряжения на π/2. Это наглядно представлено на следующем рисунке. Im = Um/(ωL).  Введем обозначение XL = ωL. Эта величина называется индуктивное сопротивление.

Контрольные вопросы:

1.Что называется переменным током?

2. Принцип создания синусоидальной ЭДС.

3. Параметры, характеризующие синусоидальную величину.

4. Виды сопротивлений в цепи переменного тока.

Скачано с www.znanio.ru