Оценка значений квадратных корней_Методические рекомендации к уроку №8

Методические рекомендации к проведению урока

Тема урока: Вычисление и оценка значений квадратных корней

Тип урока: Урок закрепления знаний

Цели обучения:

8.1.2.2

оценивать значение квадратного корня;

Цели урока:

Учащиеся могут

·         вычислять значения квадратных корней с заданной точностью, в том числе с применением калькулятора;

·      оценивать значения квадратных корней;

·      сравнивать значения квадратных корней.

Структура урока

1.    Организационный момент. Целеполагание.

2.    Мотивационный момент.

3.   Повторение пройденного материала.

4.   Решение прикладных задач.

5.   Тест.

6.   Работа в группах.

7.   Самостоятельная работа.

8.   Подведение итогов урока.

Теоретический материал к уроку, определения к понятиям и др.

Пример. Вычислим приближенное значение .

В ходе вычисления будем использовать следующую теорему:

Если , то .

Будем рассуждать следующим образом. Число  больше 1, так как 1² < 2.

В тоже время, число  < 2, так как 2² больше 2. Следовательно, десятичная запись числа будет начинаться следующим образом: 1,… То есть корень из двух, это единица с чем-то: 1<<2.

Теперь попытаемся отыскать цифру десятых. Для этого будем дроби от единицы до двойки возводить в квадрат, пока не получим число большее двух. Шаг деления возьмем 0,1, так как мы ищем число десятых. Другими словами, будем возводить в квадрат числа: 1,1; 1,2; 1,3; 1,4;1,5; 1,6;1,7; 1,8;1,9

1,1² =1,21;

1,2²=1,44;

1,3²=1,69;

1,4²=1,96;

1,5²=2,25.

Получили число превышающее двойку, остальные числа уже не надо возводить в квадрат. Число 1,4² меньше 2, а 1,5² уже больше двух, то число  должно принадлежать промежутку от 1,4 до 1,5 (1,4<  < 1,5). Следовательно, десятичная запись числа  в разряде десятых должна содержать 4. =1,4… Иначе говоря,  это число большее 1.4, но не превышающее 1.5.

Далее ищем цифру сотых, точно таким же образом. Возводим в квадрат числа от 1,41 до 1,49, с шагом 0,01, пока не получим число большее двух.

1,41²=1,9881, 1,42²=2,0164.

Уже при 1,42 получаем, что его квадрат больше двух, далее возводить в квадрат числа не имеет смысла.

Из этого получаем, что число будет принадлежать промежутку от 1,41 до 1,42 (1,41< < 1,42).

Так как нам необходимо записать  с точностью до двух знаков после запятой, то мы уже можем остановиться и не продолжать вычисления.  ≈ 1,41. Это и будет ответом. Если бы необходимо было вычислить еще более точное значение, нужно было бы продолжать вычисления, повторяя снова и снова цепочку рассуждений.

 Данный прием позволяет извлекать корень с любой заданной наперед точностью.

Инструкции к демонстрациям и технике безопасности.

Демонстрация материала осуществляется с помощью презентации PowerPoint. Слайды презентации содержат анимации, которые позволяют поэтапно вывести на экран ответы на задания для организации самооценивания и взаимооценивания. Поэтому при показе слайдов следует делать паузы после демонстрации задания или вопросов, чтобы дать учащимся возможность выполнить задания и обдумать ответы на вопросы.

Задания, оформленные отдельным приложением, несмотря на то, что они включены в презентацию, необходимо предоставить учащимся обязательно в распечатанном виде.  А имеющиеся слайды использовать при обсуждении с классом и при оценивании выполненной работы. Это поможет свести к минимуму использование интерактивной доски.

Дополнительные методические рекомендации по организации урока.

Структура и организация урока нацелены на продуктивную деятельность учащихся при закреплении пройденного материала, не допуская пассивного восприятия материала. В связи с этим учителю необходимо задавать учащимся вопросы высокого порядка, способствующие закреплению изученного материала, при этом выдерживая паузы, необходимые для обдумывания.    

Дополнительные разноуровневые (на дифференциацию) задания.

Базовый уровень

Продвинутый уровень

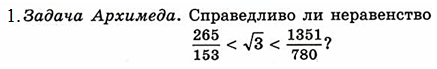
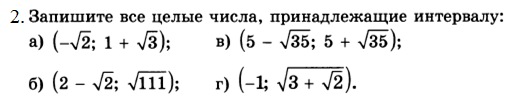
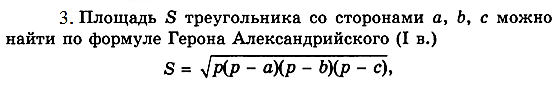
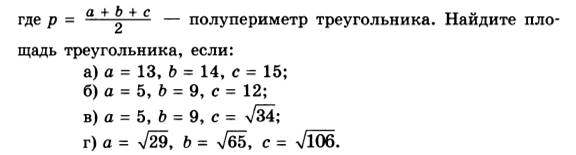
Рекомендации по формативному оцениванию.

Формативное оценивание производится на всех этапах урока (самооценивание, взаимооценивание, оценивание учителем по критериям, а также посредством наблюдения). Оценка путем наблюдения за вовлечением учеников в работу при выполнении заданий и за участием в диалогах. Прогресс, ответную реакцию на задания в группах, парах необходимо отслеживать для того, чтобы оценить вклад каждого ученика и выявить наличие ошибок для их дальнейшей коррекции.

Учитывая результаты оценивания на всех этапах урока, в том числе, по итогам самостоятельной работы, учителем будет сделан вывод о достижении цели учащимися.

Ответы, критерии к заданиям, дополнительные материалы к уроку.

Ответы к заданиям для повторения, а также к прикладным задачам из приложения 1 содержатся в презентации.

Критерии оценивания к каждому заданию прописаны в приложениях к уроку, а также указаны в краткосрочном плане.

Ответы к приложению 2.

Итоги теста

0-5 баллов – «Тебе требуется помощь учителя!»

6-8 баллов – «Повтори пройденный материал самостоятельно»

9-10 баллов – «Отличный результат, но не расслабляйся!»

Ответы к приложению 3.

1. ; ; .

2. .

3. Зная приближенное значение , вычислите приближенно (не используйте калькулятор). Ответ обоснуйте.

1) 0,8163…;   2) 1,2245;       3) 0,61225…;    4) 0,2721….

Ответы к приложению 4.

1. 13 целых чисел: -11; -10; -9; ... 0; 1.

2.  2015 и 2016.

Список полезных ссылок и литературы.

1)      https://infourok.ru/urok_algebry_v_8_klasse_po_teme-482972.htm

2)      http://edu.alnam.ru/book_b_alg.php?id=93

Скачано с www.znanio.ru