Педагогический проект «Организация работы с одарёнными детьми на уроках математики»

 

 

 

 

 

 

 

 

 

 

 

 

 

 

ПЕДАГОГИЧЕСКИЙ ПРОЕКТ

 

 

«ОРГАНИЗАЦИЯ РАБОТЫ

С ОДАРЕННЫМИ ДЕТЬМИ

НА УРОКАХ МАТЕМАТИКИ».

 

 

 

 

 

 

 

 

 

 

Введение

     При традиционном обучении нет возможности адаптироваться к индивидуальным особенностям учащихся во время урока, и одаренный ребенок оказывается вне поля зрения. И постепенно любознательность, познавательные потребности, особенно в старших классах, угасают, потому что одаренный ребенок по уровню познавательного развития опережает своих сверстников. Поэтому возникает особая форма организации работы с одарёнными учащимися, нацеленная на обосно­вание принципиально новой системы образования детей повышенного уровня обучаемости.

     Реформы, произошедшие в отечественной системе образования за

последнее десятилетие, ее направленность на гуманистическое, личностно-

ориентированное и развивающие технологии изменили отношение к

учащимся, проявляющим неординарные способности. Постепенно в

общественном сознании начинает формироваться понимание того, что

переход в век наукоемких технологий невозможен без сохранения и

умножения интеллектуального потенциала общества.

В цивилизованном мире одаренные дети существовали  всегда, независимо от того  обращали на них внимание или нет. Новыми задачами современного образования стали: отход от «среднего» ученика, повышенный интерес к одаренным, талантливым детям, раскрытие и развитие внутреннего потенциала, способностей каждого ребенка в образовательном процессе.  Нормативно – правовой основой реализации направления « Одаренные дети» является Федеральная программа «Дети России», система поддержки талантливых детей. Одновременно с реализацией стандарта общего образования должна быть выстроена система поиска и поддержки талантливых детей, а также сопровождения их в течение всего периода становления личности.

Цель:

·       Организация работы с учащимися, имеющими повышенный уровень мотивации, включение учащихся в исследовательскую  деятельность.

·       Воспитание ученика как личности компетентной, успешной и востребованной обществом.

·       Развитие у обучающихся интереса к творческой и исследовательской деятельности, к выполнению сложных заданий, способности мыслить творчески, а также укрепление в них уверенности в своих силах.

Задачи:

·       формирование у учащихся устойчивого интереса к математике;

·       выявление и развитие математических способностей;

·       овладение конкретными математическими знаниями, необходимыми для применения  в практической деятельности;

·       интеллектуальное развитие учащихся, формирование качеств мышления, характерных для математической деятельности;

·       использовать индивидуальный подход в работе с одаренными учащимися на уроках   математики и во внеурочное время с учетом возрастных и индивидуальных особенностей детей;

·       вовлекать учащихся в различные внеурочные конкурсы, интеллектуальные игры, олимпиады, позволяющие учащимся проявлять свои возможности.

Методы исследования:

·       Анализ методической и учебной литературы;

·       Изучение передового опыта учителей;

·       Работа с тестами разного уровня  и олимпиадными заданиями.

Сроки проекта:

Внедрение проекта выполнимо в течение 2016-2018 гг. но данный проект не может ограничиваться календарными сроками, так как процесс выявления развития и поддержки одарённых детей является непрерывным.

Участники проекта: Учащиеся

 

 

Актуальность:

Устойчивый интерес к математике начинает формироваться в 14 -15 лет.  Но это не происходит само собой: для того, чтобы ученик 5, 6 или 7 класса начал всерьез заниматься математикой, необходимо, чтобы на предыдущих этапах он почувствовал, что размышления над трудными, нестандартными задачами могут доставлять радость. Решение олимпиадных задач позволяет учащимся накапливать опыт в сопоставлении, наблюдении, выявлять несложные математические закономерности, высказывать догадки, нуждающиеся в доказательстве. Тем самым создаются условия для выработки у учащихся потребности в  рассуждениях, учащиеся учатся думать.  Для подтверждения своей успешности учащиеся могут участвовать в районных, областных и Всероссийских олимпиадах, вести  исследовательскую, самостоятельную  работу, по итогам которой оформлять рефераты, исследовательские работы  и проекты. Одним из важных показателей успешности работы учителя с одарёнными детьми является, конечно, результативность ГИА и ЕГЭ. Сюда можно добавить поступление выпускников в ВУЗы.

Предполагаемые продукты:

·       Разработки уроков с использованием технологии разноуровневого и проектного  обучения; использования методики обучения в малых группах.

·       Развитие творческого мышления путем решения нестандартных и проблемно-поисковых задач.

·       Организация работы в рамках дополнительного образования.

Конечный результат:

·       Повышение устойчивого интереса к предмету.

·       Умение организовать учебную деятельность.

·       Умение ставить цели и анализировать результат.

·       Участие в исследовательской деятельности, олимпиадах, интеллектуальных играх и т.д.

·       Потребность в новой информации и умение работать с дополнительной литературой.

·       Потребность к общению, обсуждению проблемы в коллективе.

Объектом исследования является организация системы работы учителя математики с одаренными детьми, а предметом исследования – поиск форм и методов обучения, технологическая и психологическая подготовка, необходимая для развития и совершенствования творческого потенциала, увеличения количества одаренных детей.

 При всех существующих трудностях в системе общего среднего образования (отсутствие методических пособий для работы с одаренными; методик проведения диагностики; трудоемкость создания индивидуальных заданий; проблема  оценки результатов), сегодня открываются новые возможности для развития личности учащегося и одаренной личности в частности.

Проект предусматривает системную целенаправленную работу с одаренными детьми 5-7 классов

Организация работы с одаренными детьми

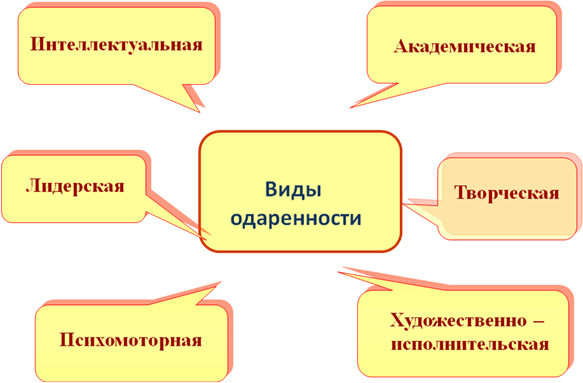
Одаренный ребенок – это ребенок, который выделяется яркими, очевидными, иногда выдающимися достижениями (или имеет внутренние предпосылки для таких достижений) в том или ином виде деятельности.

Три категории одаренных детей:   

—   Дети с необыкновенно высоким общим уровнем умственного развития (такие дети чаще всего встречаются в дошкольном и младшем школьном возрасте).     

—  Дети с признаками специальной умственной одаренности – в определенной области науки (подростковый образ).  

—   Учащиеся, не достигающие по каким-либо причинам успехов в учении, но обладающие яркой познавательной активностью, оригинальностью психического склада, незаурядными умственными резервами (чаще встречаются в старшем школьном возрасте).

       Получив пятый класс, я, как все учителя, выявляю одаренных детей, начинаю кропотливую работу по развитию способностей детей с использованием интерактивных технологий, ведь все дети, в основном, способны в той или иной области. И развитие одаренности в одной области влекут в той или иной мере развитие  способностей в других областях, хотя и неравномерно (как бы нам этого не хотелось).

Эта работа идет в трех направлениях. Постоянный подбор задач, которые решаются различными способами, выделяя оптимальный способ. Решение задач повышенной сложности в освободившееся время на уроках  и внеурочное время. Проведение кружковой работы с классом, которая выявит способных «раскрутиться». Привлечение детей к олимпиадам, турнирам, играм.

В работе с одарёнными учащимися очень важная роль отводится индивидуальной работе на уроке и во внеурочное время. Пока учащиеся на уроке работают самостоятельно можно работать в индивидуальном режиме с отдельными учениками. Но этого не достаточно.

Для целенаправленной подготовки учащихся к участию в олимпиаде необходимо рассматривать на дополнительных занятиях, факультативах,  или предлагать для самостоятельного обучения по дополнительной литературе, различные типы олимпиадных задач:

• логические задачи,
• математические ребусы,
• геометрические задачи (на разрезание и др.),
• арифметические задачи, текстовые задачи: решаемые с конца, на переливание, взвешивание, на движение, выигрышные ситуации.

       В 7 – 8 классах активно работаю на уроках и во внеурочное время с группой учащихся. В 7, 8, 9 классах начинаю индивидуальную работу по подготовке к НПК. Эта задача сложная для любого учителя, а желание детей к научной работе уже пробуждается. Вот здесь любому учителю необходима помощь ВУЗовских преподавателей, а её как правило, нет. Надо искать! Каждый раздел алгебры завершается решением задач повышенной сложности, которые включаются и в контрольные работы с последующим разбором задач.

Методы работы:

-       анкетирование, опрос;

-       собеседование;

-       тестирование;

-       анализ научных источников;

-       творческие работы;

-       метод прогнозирования;

-       метод исследования проблемы.

Формы работы с одаренными учащимися:

-       творческие мастерские;

-       групповые занятия с сильными учащимися;

-       интеллектуальные конкурсы;

-       интеллектуальный марафон;

-       участие в олимпиадах;

-       научно-исследовательские конференции;

-       членство в ученических научных обществах.

Направления:

1.     Диагностика обучающихся – оценка общей одаренности.

2.     Работа со способными и одаренными детьми на уроках.

3.     Использование системы заданий повышенной сложности:

-       задания на развитие логического мышления, нахождение общего, частного, промежуточного понятий, расположение понятий от более частных к более общим.

-       задания на развитие творческого мышления – выполнение творческих работ обучающимися.

-       задания на составление учебных проектов.

-       задания на прогнозирование ситуаций.

4.     Внеклассная работа с обучающимися – создание постоянных (НОУ) и временных групп (групп по подготовке к олимпиадам, конкурсам, конференциям)  с учетом интересов учащихся.

5.     Основной принцип работы – принцип «обогащения».

 

Ресурсное обеспечение:

-       наличие учебной аудитории;

-       библиотечный фонд – наличие литературы;

-       цифровые ресурсы – ИКТ.

Критерий эффективности:

1.     Высокий уровень познавательного интереса к предмету.

2.     Отсутствие неуспевающих по предмету.

3.     Увеличение количества обучающихся, выбирающих предметы естественно-математического цикла как экзамен с успешной его сдачей.

4.  Учащиеся становятся призерами олимпиад и конкурсов.

 

 

 

 

Этапы работы

I этап – аналитический – при выявлении одаренных детей учитываются их успехи в какой-либо деятельности. Творческий потенциал ребенка может получить развитие в разных образовательных областях, но наиболее естественно, сообразно предмету – в области математического развития. В связи с этим следует вовлекать учащихся в различные виды умственной, поисково-познавательной и творческой деятельности.

II этап – диагностический – индивидуальная оценка познавательных, творческих возможностей и способностей ребенка. На этом этапе проводятся групповые формы работы: конкурсы, «мозговые штурмы», ролевые тренинги, научно-практические работы, творческие зачеты, проектные задания, участие в интеллектуальных олимпиадах, марафонах, проектах.

III этап – этап формирования, углубления и развития способностей учащихся. С этой целью в школе организовано научное общества учащихся «Прометей», куда вошли самые активные, самые творческие, самые любознательные, самые трудолюбивые и способные в разных областях знаний и цикла естественно-математических наук ребята

Принципы работы с одаренными детьми:

·       Принцип дифференциации и индивидуализации обучения.

·       Принцип максимального разнообразия предоставляемых возможностей.

·       Принцип возрастания роли внеурочной деятельности одаренных детей.

·       Принцип усиления внимания к проблеме межпредметных связей в индивиду­альной работе с учащимися.

·       Принцип создания условий для совместной работы учащихся при минимальной роли учителя.

 

 

 

 

 

 

 

 

 

 

Условия успешной работы с одаренными учащимися

      Осознание важности работы с одаренными детьми каждым членом коллектива и усиление в связи с этим внимания к проблеме формирования положительной мотивации к учению.

1)    Создание и постоянное совершенствование методической системы работы с одаренными детьми.

2)    Признание коллективом педагогов и руководством школы того, что реализация системы работы с одаренными детьми является одним из приоритетных направлений работы школы.

       Поэтому учителю в своей работе необходимо регулярно использовать дифференциацию и индивидуализацию в обучении.  Прежде всего, важно изучить индивидуальные особенности учеников в классе. Затем работать в трех направлениях:

I - разноуровневый подход к детям

Использовать разноуровневые задания (обучающие и контролирующие). Использовать разноуровневые задания необходимо не только на уроках, но и в виде домашнего задания.

II - обучение самостоятельной работе

Учить работать самостоятельно с учебником, с дополнительной литературой, проводить исследовательскую работу.

 III -обучение исследовательской работе.

       Использование задач с элементами исследования, развивающие задачи. Такие задания можно предлагать, как дополнительные(т. е. не обязательные для выполнения) всему классу, но для одарённых учащихся эти задания являются обязательными (выполнение таких заданий оценивается оценкой «5», если учащимся допущена ошибка, то оценка не выставляется.)  Систематически предлагать учащимся творческие задания: составить задачу, выражение, кроссворд, ребус, анаграмму и т. д. Учить учащихся, как проанализировать полученную информацию, выделить главное, исключить второстепенное. И, наконец, в каком виде представить результат. Это может быть электронная презентация или документ, макет, книжка-раскладушка и т.д.  Большую возможность в этом направлении даёт разработка проектов. Выбор темы проекта должен быть полезен участникам исследования. Тема должна быть интересной учащимся. Она должна быть доступной, и проблема должна соответствовать возрастным особенностям детей - сочетание желаний и возможностей (нужно учесть наличие необходимых средств и материалов). Но самое главное - это защита. Защита - это венец исследовательской работы. Она должна быть публичной. В ходе ее ребенок учится излагать добытую информацию, сталкивается с другими взглядами на проблему, учится доказывать свою точку зрения. На первых этапах защита проекта проходит в классе. Самые интересные и лучшие работы идут на школьную конференцию.  

Исследовательская работа активизирует обучение, придает ему творческий характер и таким образом передает учащимся инициативу в организации своей познавательной деятельности развития творческих способностей.

       Примечание. В каждой работе должна быть проведена систематизация материала, историческая справка и свои выводы по теме проекта. Поэтому работа над проектом предполагает сбор материала, его систематизацию, обоснование и суждения автора. При работе над проектом автор должен приобрести  компетентность в области проектной темы. Материал должен быть подготовлен к защите проекта.

 

Признаки наличия математических способностей у ребенка

—  Быстрое овладение математическими знаниями, умениями и навыками.

—  Быстрота понимания объяснения учителя.

—  Логичность, самостоятельность мышления.

—  Находчивость и сообразительность при изучении математики.

—  Быстрое и прочное запоминание материала.

—  Высокая степень развития способности к обобщению, анализу и синтезу  математического материала.

—  Пониженная утомляемость при занятиях математикой.

—  Способность быстро переключаться с прямого на обратный ход мысли.

 

Можно условно выделить несколько групп детей с учётом уровня и характера их мотивации. Это помогает в выборе приемов педагогической поддержки

1)»Мотивация на результат» (такие дети не умеют радоваться успехам других, болезненно переживают свои неудачи и готовы «расталкивать всех локтями» для достижения цели; здесь необходима индивидуальная работа психолога)

2)»Мотивация на самоутверждение» (их психологическая защита строится на тезисе «скучно, неинтересно», они также не любят успехов других, но они способны признавать высокий профессионализм педагога; основной прием поддержки  в данной ситуации «косвенная аналогия», создание ситуаций, где ученик смог бы увидеть себя)

3)»Мотивация на творчество» (такие дети не любят фактической стороны учения, но могут выдавать нестандартные идеи и мысли; для подобных детей необходимо обучение самоконтролю, самоорганизации)

4)»Мотивация на познание» (такие дети требуют индивидуальной программы обучения; задача педагога-наставника не «культивировать» свой предмет, а помочь ученику увидеть и понять картину мира, понять значимость интегрального знания

Методические и теоретические основы работы учителя с одаренными детьми

При выявлении детей с незаурядными умственными возможностями встает проблема, чему и как их научить, как способствовать их оптимальному развитию. Программа для одаренных детей должна отличаться от обычной учебной программы. Обучение таких детей должно отвечать их существенным потребностям. Одаренные дети обладают некоторыми общими особенностями,  и которые должны учитываться. К таким особенностям относятся следующие:

-  способность быстро схватывать смысл принципов, понятий положений.    Такая особенность требует широты материала для обобщения.

-  потребность сосредотачиваться на заинтересовавших сторонах проблемы и   стремлении разобраться в них. Эта потребность редко удовлетворяется при    традиционном обучении, и ей надо дать реализоваться через  самостоятельную работу, задания открытого типа, развитие необходимых    познавательных умений.

-  способность подмечать, рассуждать и выдвигать объяснения.

-  обеспокоенность, тревожность в связи со своей непохожестью на    сверстников. Включение в учебную программу активного компонента дает     возможность ребенку лучше понять себя и свои переживания и приведет к     принятию себя и других.

Существуют различные стратегии обучения одаренных детей, которые могут быть воплощены в различные формы. Их можно разделить на 4 этапа.

1 этап – подготовительный. Основная цель его подготовить условия для формирования системы работы с одаренными детьми в школе. Он включает в себя диагностику по следующим направлениям:

·       Творческое мышление.

·       Уровень самооценки.

·       Толерантность.

·       Предпочтительные виды деятельности.

·       Доминирование правого или левого полушарий.

·       Сила интуиции

·       Лидерство.

·       Гениальность.

·       Карта интересов.

·       Диагностика задатков и склонностей личности.

·       Поведенческие характеристики одаренных детей.

По итогам данного этапа можно выделить три категории одаренных детей:

1.     Дети с высоким общим уровнем умственного развития при прочих равных условиях (такие дети чаще всего встречаются в младшем школьном возрасте).

2.     Дети с признаками специальной умственной одаренности в определенной области науки (подростковый возраст).

3.     Учащиеся, не достигающие по каким-либо причинам успехов в обучении, но обладающие яркой познавательной активностью, оригинальностью психологического склада, незаурядными умственными резервами (чаще встречаются в старшем школьном возрасте).

1 ступень (начальная школа) – при выявлении одаренных детей учитываются

 их успехи в какой-либо деятельности. Этот этап характеризуется тем, что

 дети охотно осваивают навыковое содержание учения под руководством

 учителя и самостоятельно. На этом этапе очень важно организовать урочную

 и внеурочную деятельность как единый процесс, направленный на развитие

познавательных способностей учащихся.

2ступень (5-9 классы) – на этом этапе проводится индивидуальная оценка

познавательных, творческих возможностей и способностей ребенка через

различные виды деятельности: учебную и внеклассную.

Содержание работы с одаренными детьми определяется в рамках каждой из

 учебных дисциплин. Содержание учебного материала должно настраивать

учащихся на непрерывное обучение, процесс познания должен быть для

 таких детей самоценным.

3ступень. Старшая школа является образовательным пространством, в

рамках которого, с одной стороны, завершается выполнение обществом его

обязательной функции по формированию социально-адаптированной

личности, а с другой стороны, реально происходит постепенная

переориентация доминирующей образовательной парадигмы с

преимущественной трансляцией системы ЗУНов к созданию условий для

комплекса компетенций, которые рассматриваются как способности

человека реализовать свои замыслы в условиях многофакторного

информационного коммуникационного пространства. Исходя из этого

формируются новые принципы и методология организации

образовательного пространства в школе:

·       выработка проектно-исследовательских навыков (проектная методика);

·       самоопределение старшеклассников в отношении профильного направления собственной деятельности;

На 2 этапе нужен постепенный переход к обучению не столько фактам, сколько идеям и способам, развивающим мышление, побуждающим к

самостоятельной работе, ориентирующим на дальнейшее

самосовершенствование и самообразование, постепенное проявление той

цели, для достижения которой они прилагают столько духовных,

интеллектуальных и физических усилий. На этом этапе с одаренными

детьми наиболее целесообразны групповые формы работы. Важным

фактором, влияющим на развитие одаренных учащихся и на выявление

скрытой одаренности и способностей, является система внеклассной работы

в школе. Условиями для успешной работы с одаренными являются:

-  принцип максимального разнообразия представленных возможностей для

    развития личности;

-  принцип возрастания роли внеурочной деятельности;

-  принцип индивидуализации и дифференциации обучения;

-  принцип создания условий для совместной работы учащихся при

    минимальном участии учителя;

-  принцип свободы выбора учащимся дополнительных образовательных  услуг, помощи, наставничества.

       Основными технологиями в работе с одаренными детьми на этом этапе

являются:

1.      Технология проблемного обучения. Эту технологию мы будем

рассматривать как базовую, поскольку преобразующая деятельность

ученика может быть наиболее эффективно реализована в процессе

выполнения заданий проблемного характера. Как показывает опыт,

 решение задач проблемного содержания обеспечивает высокий

уровень познавательной активности учащихся. Структура процесса

проблемного обучения представляет собой комплекс взаимосвязанных

и усложняющихся ситуаций. Реализуя технологию проблемного

обучения, учитель чаще всего использует проблемные вопросы в

форме познавательной (проблемной) задачи. Алгоритм решения

проблемной задачи включает в четыре этапа:

·       Осознание проблемы, выявление противоречия, заложенного в вопросе, определение разрыва в цепочке причинно-следственных связей;

·       Формирование гипотезы и поиск путей доказательства предположения;

·       Доказательство гипотезы, в процессе которого учащийся переформулирует вопрос или задание;

·       Общий вывод, в котором изучаемые причинно-следственные связи являются и выявляются новые стороны познавательного объекта или явления.

     Таким образом, совокупность целенаправленных сконструированных задач,

создающих проблемные ситуации, призвана обеспечить главную функцию

проблемного обучения – развитие умения мыслить на уровне взаимосвязей и

зависимостей. Это позволяет школьникам приобрести определенный опыт

творческой деятельности, необходимый в процессе ученических

исследований.

2.      Методика обучения в малых группах.  Суть обучения в «малых

группах» заключается в том, что класс разбивается на 3-4 полгруппы.

Каждая из них готовит ответ на один из обсуждаемых вопросов, при

обсуждении которых участники оппонируют, рецензируют и делают

дополнения. Игровая ситуация позволяет создать необходимый

эмоциональный настрой и побудить школьников к более напряженной

и разнообразной работе.

3.      Технология проектного обучения. В основе системы проектного

обучения лежит творческое усвоение школьниками знаний в процессе

самостоятельной поисковой деятельности, то есть проектирования.

Продукт проектирования – учебный проект, в качестве которого могут

выступать реферат, доклад, исследовательская работа. Важно, что

проектное обучение по своей сути является личностно

ориентированным, позволяет школьникам учиться на собственном

опыте и опыте других. Это стимулирует познавательные интересы

учащихся, дает возможность получить удовлетворение от результатов

своего труда, осознать ситуацию успеха в обучении.

3этап  - организационно - деятельный, целью которого является организация

целенаправленной работы с одаренными детьми.

4 итоговый этап – этап формирования, углубления и развития способностей

учащихся.  Основная цель его апробация системы с одаренными детьми.

 

 

 

 

 

 

 

 

Решение нестандартных и поисковых задач в системе работы с

одаренными детьми.

      При работе с учащимися 5-7 классов учителю необходимо учитывать

возрастную категорию. Чтобы создать комфортные условия на уроке, нельзя

резко проводить границы между одаренными, средними и слабыми

учащимися, на этом этапе это может привести к тому, что многие ребята

потеряют интерес к предмету и не смогут раскрыть свой потенциал.

Работу с учащимися можно рассматривать как систему методов и приемов

при организации деятельности на уроке, внеурочной школьной деятельности

и внешкольной деятельности.

       Основным принципом работы учителя является личностно

ориентированный подход, который является неотъемлемой частью при

организации самостоятельной работы учащихся. Эту работу необходимо

планировать с учетом индивидуально-дифференцированного подхода в

процессе обучения. Объемный материал содержат пособия по математике

«Самостоятельные и контрольные работы» А.П. Ершов, В.В. Голобородько,

М. ИЛЕКСА  5- 11 классы, где представлены не только задачи для

самостоятельного решения разных уровней, что позволяет учителю

организовать систематическую самостоятельную работу, учитывая уровень

возможностей учащихся, но и нестандартные задачи по различным темам.

Нестандартная задача – это задача, алгоритм решения которой учащимся

неизвестен, т.е. учащиеся не знают заранее ни способа ее решения, ни того,

на какой учебный материал опирается решение. Научить решать такие задачи

можно только в том случае, если у учащихся будет желание их решать, т.е.

задачи будут содержательными и интересными с точки зрения ученика.

Учитель должен вызвать интерес к задаче, убедить ученика, что от решения

математической задачи можно получать такое же удовольствие, как при

разгадывании ребуса.

       Применение задач повышенной сложности и нестандартных задач

достаточно широко. Они могут быть использованы при закреплении новой

темы.

       Целью обучения математики в школе является не только овладение конкретными математическими знаниями, но и интеллектуальное развитие учащихся, формирование качеств мышления, характерных для математической деятельности и необходимых человеку для продуктивной жизни в обществе. В настоящий момент образование характеризуется как процесс обучения и воспитания в интересах личности, общества и государства, направленный на развитие индивида, его индивидуальных, умственных и физических способностей, одаренности и таланта.

  

 

 

 

 

 

 

 

 

 

 

 

 

 

5 класс  тема: «Квадрат и куб числа»

Тип урока -  отработка навыков решения задач.

Оборудование: проектор

Задача:

Число дней в не високосном году 365. Это число обладает рядом интересных

свойств. Оно равно сумме квадратов (меньших 20) чисел. Найдите их

При работе используется работа в парах.

Самый быстрый результат рассматривается на доске.

Вывод: Это число можно разложить двумя способами:

365= 10² +11² +12²      или    365=13²  +14².

 

 

 

 

 

Алгебра 7 класс  тема: «Разложение на множители»

Тип урока – закрепление методов разложения многочлена на множители.

Задача:Какое наибольшее слагаемое надо добавить, чтобы сумма 

x+у+z+ху+хz+уz+хуz, разлагалась на произведение трех множителей. Какие

это множители?

При решении используется индивидуальная работа.

Обсуждение на доске:

Добавить 1. (1+х)(1+у)(1+z)= 1+x+у+z+ху+хz+уz+хуz.

Нестандартные задачи приобщают учащихся к деятельности творческого

характера, способствуют развитию интереса к математике, трудолюбия,

упорства в достижении цели. Нестандартные задачи можно разделить на три

группы:

1)     Задачи, которые целесообразно решать со всем классом

2)    Задачи , которые полезно задавать на дом в качестве необязательного задания, их решение рассмотреть во внеурочное время с заинтересованными учащимися

3)    Задачи для внеклассной работы

Таким образом, нестандартные задачи служат переходным мостиком от

классной работы к внеклассной. В процессе этой работы одаренные

учащиеся выступают как лидеры, генераторы идей, а также в роли учителя.

В систему работы с одаренными учащимися на уроке математики входят

обязательным образом решение поисковых задач, создание различных

проблемных ситуаций. Навыки решения поисково- исследовательских задач нужно формировать систематически не только на уроках , но и во

внеурочное время. Успех привития навыков решения во многом зависит от

контроля. Не жесткий контроль, а заинтересованность учащихся могут

формировать навыки решения и положительное отношение к ним. В основе

этого должны лежать положительные мотивы обучения, интерес к

познавательному процессу, исследовательской деятельности, к самостоятельному добыванию знаний.

Алгебра 7 класс  тема: «Формулы сокращенного

умножения»

Тип урока – введение нового материала. Данный фрагмент представляет

собой исследовательскую работу учащихся, направленную на выведение

общей формулы суммы и разности двучлена. Исследовательская работа не

только вызывает интерес у ребят, но и развивает их умение работать в

коллективе.

Оборудование: таблица. 

Учитель, сообщая цель урока, обращает внимание на то, что еще в глубокой

древности было подмечено, что некоторые многочлены можно умножать

короче, быстрее, чем все остальные. Так появились формулы сокращенного

умножения. И сегодня вам предстоит сыграть роль исследователей в

открытии двух из этих формул.

Для работы используется работа в малых группах. Учащие выполняют

умножение двучленов, после чего они записывают результаты в правой части

таблицы, средняя часть скрыта.

Таблица.

1)     (х+у)(х+у)=(х+у)²=х²+2ху+у²

2)    (с+р)(с+р)=(с+р)²=  с²+2ср+р²

3)    (к+в)(к+в)=(к+в)²=  к²+2кв+в²

4)    (2+х)(2+х)=(2+х)²= 4+4х+х²

После заполнения таблицы, учитель просит найти закономерности.

Ребята замечают, что правая часть трехчлен, и выводят формулу.

 

 

 

 

 

 

 

Геометрия 7 класс  тема: «Сумма углов в

треугольнике»

Тип урока – объяснение нового материала. Цель- сформулировать и доказать

теорему о сумме углов в треугольнике.

Оборудование: чертеж.

Учитель ставит перед учащимися проблемы: 1. Как найти сумму углов

треугольника; 2. Как не измеряя, доказать, что их сумма 180 градусов.

Отложив углы А и В от сторон угла С по разные стороны от него, получим

угол MCN. Нужно доказать, что он развернутый.

Из равенства внутренних накрест лежащих углов СВА и NCB , углов СВА и

МСА следует параллельность прямых СМ и АВ; СN и АВ, по аксиоме

параллельных прямых, СМ и  СN совпадают. Угол MCN – развернутый.

2. Замечаем, что угол В сам отложился: СМ // АВ, поэтому углы СВА и NCB

равны, как накрест лежащие.

3.Наконец,  угол NCB можно не рассматривать. Отложив угол А и доказав,

что СМ//АВ, замечаем, что А+В+С=МСВ+В=180, как сумма внутренних

односторонних при  СМ // АВ и секущей СВ.

Решив данную проблему, учащиеся приходят к самостоятельному

доказательству теоремы.

5 класс тема: «Единицы площади»

Тип урока – актуализация знаний.

Цель - установит соответствие между единицами измерения площади.

Оборудование: мел, доска.

Создание проблемной ситуации: рассмотрите запись на доске:

500м²;  400см²;  3а; 2дм²; 7га.

Расположите их в порядке возрастания.

В чем сложность проблемы? Чем они являются? Какова тема урока?

 

 

 

 

 

 

 

Внеклассная работа с одаренным детьми

       Анализ учебников математики показывает, что не один из учебников не содержит необходимого набора задач, направленных на развитие одаренных учащихся, т.е. задач на развитие различных познавательных  процессов, обеспечивающих достижение целей развития способных детей. Современные   образовательные  стандарты, программы математического образования для общеобразовательной школы лишь отмечают развивающие возможности математики, но не уделяют внимания их использованию для развития одаренных детей в процессе обучения.

       Основным видом внеклассной работы по математике в школе являются

математические кружки. Они вызывают интерес учащихся к предмету,

способствуют расширению математического кругозора, творческих

способностей учащихся, привитию навыков самостоятельной работы.

Повышают качество общей математической подготовки учащихся.Одна из

главных целей кружка познакомить учащихся с общими подходами к

решению разнообразных задач. Большую роль играют методы графов,

полного перебора, математической индукции и другие.

Другим видом внеклассной работы с одаренными детьми является обучение

в ЗМШ «Авангард», что позволяет учащимся самостоятельно развивать и

закреплять полученные знания.

        Целью кружковой работы является не только овладение учащимися умениями и навыками, но развитие в детях математических способностей, различных качества ума, вычислительной культуры, элементов творческой деятельности, научного мировоззрения.

       И, конечно, нельзя не остановиться на исследовательской деятельности,

которая помогает развить у учащегося способности к саморазвитию,

самообразованию; умение вступать в общение; владеть информационными

технологиями, работать со всеми видами информации; уметь работать и

создавать свой продукт.

       Основы исследовательской деятельности закладываются на уроках.

Самостоятельно и активно разбираться в новом материале учащиеся смогут,

если у них возник интерес к исследованию. При выполнении

исследовательского задания учащийся должен осуществить следующие

действия:

·       Ознакомление с содержанием задания и постановкой цели деятельности.

·       Прогнозирование направлений выполнения задания и выбор методов исследования.

·       Проведения исследования и оценка полученных результатов в соответствии с поставленными целями.

 

 

 

 

 

 

 

 

 

 

 

 

Помощь одаренным учащимся в самореализации их творческой направленности

—  создание для ученика ситуации успеха и уверенности, через индивидуальное обучение и воспитание;

—  организация научно-исследовательской деятельности;

—  организация и участие в интеллектуальных играх, творческих конкурсах, предметных  олимпиадах, научно-практических конференциях.

—  разработка и реализация межпредметных научно-исследовательских проектов.

—  изготовление компьютерных презентаций, видеороликов, исследований.

Поощрение одаренных детей

—      Публикация на сайте школы

—      Награждение

 

 

 

 

Примеры задач, используемых на занятиях  кружка

—  Акробат и собачонка весят два пустых бочонка. Шустрый пес без акробата Весит два мотка шпагата. А с одним мотком ягненок Весит - видите - бочонок. Сколько весит акробат в пересчете на ягнят?

 

 

Задача на развитие логического мышления

Жили-были две фигуры: Круг и Квадрат. На их улице было 3 дома: один дом был с окном и трубой, другой с окном, но без трубы, третий с трубой, но без окна. Каждая фигура жила в своем доме. Круг и квадрат жили в домах с окнами. Квадрат любил тепло и часто топил печку. Кто в каком доме жил?

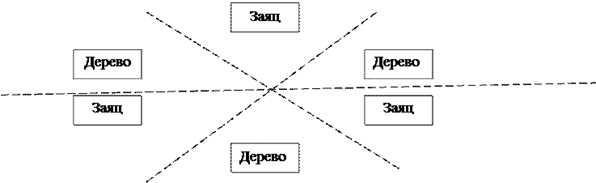
Тремя линиями отделить деревья от зайцев

Переложить 1 палочку так, чтобы домик был перевернут в другую сторону

Занимательные вопросы

—  Сколько ушей у трёх мышей?

—  Сколько лап у двух медвежат?

—  У семи братьев по одной сестре. Сколько всего сестёр?

—  У бабушки Даши внучка Маша, кот Пушок и собака Дружок. Сколько всего внуков у бабушки?

—  Над рекой летели птицы: голубь, щука, 2 синицы, 2 стрижа и 5 угрей. Сколько птиц? Ответь скорей!

—  Горело 7 свечей. 2 свечи погасили, а остальные продолжали гореть. Сколько свечей осталось? (2, остальные сгорели).

—  В корзине три яблока. Как поделить их между тремя детьми так, чтобы одно яблоко осталось в корзине? (Отдать одно яблоко вместе с корзиной).

—  На берёзе три толстых ветки, на каждой толстой ветке по три тоненьких веточки. На каждой тоненькой веточке по одному яблочку. Сколько всего яблок? (Нисколько – на берёзе яблоки не растут.)

Задачи-шутки

—  На столе три стакана с ягодами. Вова съел один стакан ягод. Сколько стаканов осталось на столе? (Три)

—  Шли двое, остановились, один у другого спрашивает: «Это черная?». – «Нет, это красная». – «А почему она белая?» – «Потому, что зеленая». О чем они вели разговор? (О смородине)

—  На столе лежат два апельсина и четыре банана. Сколько овощей на столе? (Нисколько)

—  На груше росло десять груш, а на иве на две груши меньше. Сколько груш росло на иве? (Нисколько)

—  На какое дерево сядет воробей после дождя? (На мокрое)

—  Чего больше в квартире: стульев или мебели? (Мебели)

—  Ты да я да мы с тобой. Сколько нас всего? (Два)

—  Как можно сорвать ветку, не спугнув на ней птичку? (Нельзя, улетит).

 

 

 

 

Задачи в стихах

Решила старушка ватрушки испечь.
Поставила тесто да печь затопила. 
Решила старушка ватрушки испечь,
А сколько их надо — совсем позабыла. 
Две штучки — для внучки, 
Две штучки — для деда, 
Две штучки — для Тани, 
Дочурки соседа... Считала, считала, да сбилась, 
А печь-то совсем протопилась! 
Помоги старушке сосчитать ватрушки

      (В. Кудрявцева)

 

 

 

 

 

 

 

 

Фрагмент исследовательской работы:

Применение рядов Фарея на практике.

На практике встречаются упражнения по упрощению (вычислению)

дробей, требующих много времени, если их выполнять, используя

обычные, стандартные приемы. Например, вычислить:

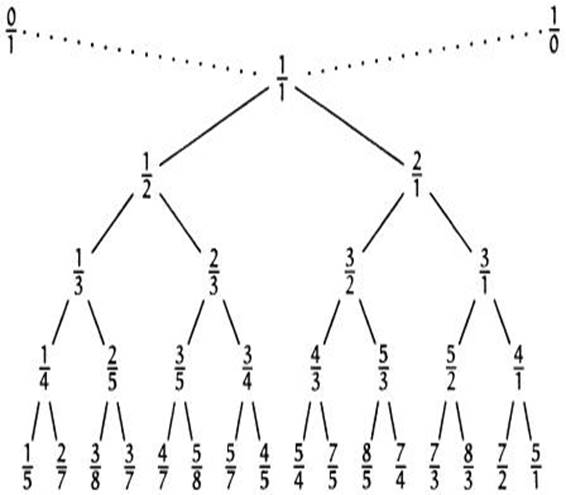
Поиск информации по данной теме привел нас к рядам Фарея.

В 1816 году была опубликована статья Фарея «Об интересном свойстве

обыкновенных дробей», в которой Фарей определил

последовательность F_n и описал то самое «интересное свойство»

итеративного построения последовательностей.

Что представляют ряды Фарея, какими  свойствами обладают, как их

получить и  использовать в решении – цель нашего проекта.

Выявление закономерности

Если выписать все правильные несократимые дроби, у которых 

знаменатель не больше 7, то получим:

,

если эти дроби расположим в порядке возрастания, то запишем

следующую последовательность дробей:

Обратим внимание на интересную закономерность: числитель разности

двух соседних дробей равен 1, а знаменатель – произведение

знаменателей (взаимно - простые числа):

И как итог работы с одаренными учащимися является участие их в

олимпиадах различного уровня: школьные, районные, международные) и

различных интеллектуальных математических играх. Результаты их и

являются итогом работы педагога.

Применение свойств при решении задач

Возвращаясь к примеру

 =

Представим дроби в виде разности соседних дробей рядов Фарея:

 =1-

В перспективе мы планируем расширить свои знания в области рядов Фарея,

а также узнать интересные факты из теории чисел, потому что многие из них

могут пригодиться  в программировании задач, решении примеров.

 

 

 

 

Рекомендации учителям в работе с одаренными детьми

—  Учителю не следует уделять слишком много внимания

     игровому обучению с ярко выраженным элементом соревнования. Одаренный ребенок будет чаще

     всего оказываться победителем, что может вызвать

     неприязнь соучеников и не благоприятствует созданию атмосферы всеобщей заинтересованности, к которой

     стремится учитель.

—  Учитель не должен возводить одаренного ребенка на

     пьедестал или делать из него вундеркинда в глазах других учеников. Успехи его будут должным образом оценены, а неуместное выпячивание его исключительности достижений рождает чаще всего раздражение, ревность и отторжение вместо ожидаемой похвалы. Другая крайность — преднамеренное публичное принижение уникальных способностей и даже сарказм со стороны учителя,— конечно, недопустима.

—  Не занимайтесь наставлениями, помогайте детям действовать независимо, не давайте прямых инструкций относительно того, чем они должны заниматься .

—  Не сдерживайте инициативы и не делайте за них то, что они могут сделать самостоятельно .

—  Научите школьников прослеживать межпредметные связи и использовать знания, полученные при изучении других предметов. 

—  Приучайте детей к навыкам самостоятельного решения проблем, исследования и анализа ситуации. 

—  Используйте трудные ситуации, возникшие в школе или дома, как область приложения полученных навыков при решении задач. 

—  Помогайте детям научиться управлять процессом усвоения знаний .

 

 

 

Цитаты об одаренности, таланте, творчестве

Гении не падают с неба, они должны иметь возможность образоваться и развиться. (А.Бебель)

Врожденные дарования подобным диким растениям и нуждаются в выращивании с помощью ученых занятий. (Ф.Бэкон)

Какой главный признак настоящего таланта? Это постоянное развитие, постоянное самосовершенствование. (В.В.Стасов)

Талант – это развитие природных склонностей. (О. Бальзак)

Ум так относится к таланту, как целое к частному. (Ж. Лабрюйер)

В каждом человеке заключается целый ряд способностей и наклонностей, которые стоит лишь пробудить и развить, чтобы они, при приложении к делу, произвели самые превосходные результаты. Лишь тогда человек становится настоящим человеком. (А. Бебель)

По-моему, талант – это прежде всего ответственность. (П.Л. Проскурин)

Я вообще не верю в одну единственную силу таланта, без упорной работы. Выдохнется без нее самый большой талант, как заглохнет в пустыне родник, не пробивая себе дороги через пески … (Ф.И. Шаляпин)

Гений – один процент вдохновения и девяносто девять процентов пота. (Т. Эдисон)

Талант в мужчине то же, что красота в женщине – всего лишь обещание. Для того, чтобы быть подлинно великим, его сердце и характер должны быть равны его таланту. (О. Бальзак)

Творчество – это не сумма знаний, а особая направленность интеллекта, особая взаимосвязь между интеллектуальной жизнью личности и проявлением ее сил в активной деятельности. Творчество – это деятельность, в которой раскрывается духовный мир личности. (В.А. Сухомлинский)

Сердце – вот истинный рычаг всего великого. (Л. Бетховен)

Что остается надолго, то рождается от цельной личности в муках и радостях, совершенно так же, как в природе рождается жизнь. (М.М. Пришвин)

Два качества необходимы художнику: чувство нравственности и чувство перспективы. (Д. Дидро)

Гениальность может оказаться лишь мимолетным шансом. Только работа и воля могут дать ей жизнь и обратить ее в славу. Труд, его упорядоченность и заложенное в нем смирение образуют, таким образом, основу свободного творчества… (А. Камю)

Где нет простора для проявления способности, там нет и способности. (Л. Фейербах)

Давно уже было замечено, что таланты являются всюду и всегда, где и когда существуют общественные условия, благоприятные для их развития. (Г.В. Плеханов)

 

 

План индивидуальной работы с одарёнными детьми

Мероприятия	Форма	Сроки проведения	Результаты
			Участники	Призовые места
Урочные и внеурочные мероприятия
Индивидуальные занятия	Консультация	1 раз в неделю
Участие в школьных предметных олимпиадах	Олимпиада по математике	1 раз в год, октябрь
Участие в районных предметных олимпиадах	Олимпиада по математике	1 раз в год, ноябрь
Участие в общероссийских конкурсах	1. Всероссийский «Молодёжный математический чемпионат!	1 раз в год, ноябрь
	2.Межрегиональная заочная физико-математическая олимпиада	1 раз в год, ноябрь
	3. Олимпиада по математике «Кенгуру»	1 раз в год, март
Участие в  научно-практической конференции учащихся.	Конференция школьников	1 раз в год, март
Участие в предметной неделе по математике.	Участие в конкурсе: составить кроссворд, ребус, анаграмму и т. д.	1 раз в год, январь
Факультативы	Групповые занятия с сильными учащимися	1 раз в неделю

       Для того чтобы работа с одарёнными была максимально эффективна необходимо выделять дополнительные часы для работы с сильными учащимися (факультативы, индивидуально-групповые занятия и т.д.).

Ожидаемые результаты:

1.Повышение качества образования.

2.Увеличение числа детей, активно занимающихся творческой, интеллектуальной деятельностью.

3. Издание исследовательских работ учащихся.

 

 

 

 

Заключение

       В заключение необходимо напомнить, что работа педагога с одаренными детьми – это сложный и никогда не прекращающийся процесс. Он требует от учителей личностного роста, хороших, постоянно обновляемых знаний в области психологии одарённых и их обучения, а также тесного сотрудничества с другими учителями, администрацией и обязательно с родителями одарённых. Он требует постоянного роста мастерства, педагогической гибкости, умения отказаться от того, что еще сегодня казалось творческой находкой и сильной стороной. Только высоко одаренные люди способны внести наибольший вклад в развитие общества, и не развивать таланты является непозволительной ошибкой для развития любого государства.

       Итак, развивать способности можно и нужно. Для этого необходимо

повернуться к личности ребенка, к его индивидуальности, создать условия

для развития и максимальной реализации его склонностей и способностей.

Необходимо создать разноуровневые и профильные программы, учебно-

методическое обеспечение, направленное на организацию

дифференцированного подхода обучения на уроках, а также на групповых и

индивидуальных занятиях с учащимися разных способностей. Активно и

заинтересованно вести внеклассную работу.

       Творчеству можно и нужно учить. И чем раньше начнется эта работа, тем

выше будут ее результаты.

       Если учитель верит в ученика, видит в нем одаренность, то эта веры творит

чудеса. И радость первого открытия, первой победы – будет общей

радостью учителя и ученика.

 

 

 

 

 

 

Оценка проекта

       Данный проект составлен на опыте работы учителя математики в 5-7

классах с одаренными детьми на уроке и во внеклассной работе.  Система

работы включает в себя гармоничное сочетание технологий проблемного

обучения, личностно ориентированного, индивидуально-

дифференцированного подходов в обучении. Основной акцент в работе

сделан на решение поисково-исследовательских задач, нестандартных задач,

а также индивидуальной  самостоятельной работы учащихся, используя

технологию проектного обучения.  При составлении работы учитывались

такие факторы, как системность, комплексность, последовательность,

нестандартность, работа на основе интереса и активности. Практика

подтверждает правильность и эффективность выбранного направления в

работе с одаренными детьми данной возрастной категории.  

 

 

 Литература:

1.     Математика. 6-9 класс. Поступаем в ВУЗ по результатам олимпиад. Часть 2./Под редакцией Ф.Ф.Лысенко. – Ростов-на Дону: Легион-М, 2009. – 112 с.

2.     Макарычев Ю. Н., Миндюк Н. Г. Алгебра: элементы статистики и теории вероятностей, 7-9 кл. – М.: Просвещение, 2008 г.

3.     Подготовка школьников к олимпиадам по математике: 5-6 классы. Методическое пособие / авт.-сост. Г.И.Григорьева. – М.: Издательство «Глобус», 2009. – 152 с.

4.     Предметная неделя математики в школе / Т.Г.Власова. – Изд. 5-е – Ростов н/Д.: Феникс, 2009. 168 с.

5.     Самое полное издание типовых вариантов заданий ЕГЭ : 2012 : Математика / авт.-сост. И.Р.Высоцкий, Д.Д.Гущин, П.И.Захаров и др.; под ред. А.Л.Семенова, И.В.Ященко. – М.: АСТ: Астрель, 2012. 93 с. – (ФИПИ 2012)

6.     Лейтес Н.С. «Возрастная одаренность школьников»,М., Академия 2000

7.     Груднев А.И. «Совершенствование методики работы учителя математики» М, Просвещение 1998

8.     Система работы образовательного учреждения с одаренными             детьми/авт.-сос. Н.И. Пантина и др. – Волгоград: Учитель

9.     Березин В.Н. Сборник задач для факультативных и внеклассных

     занятий по математике, М Просвещение 1985