PHY_10_2_V1_TG_Physical measurements

THEORETICAL MATERIALS FOR LESSON

·         Reproducibility 
All measurements that are made to the limits of the measuring device necessarily involve some estimation of the final digit in the value for the measured quantity. If this doesn't appear to be the case as in some instruments with digital outputs, it is because the meter is rounding for you and the true limit of "precision" for the instrument is being obscured by this rounding. In any case, reproducibility in measurements is a critical aspect of the measurements and often is reported. In engineering or production this is commonly referred to as "the tolerance." For example, furniture construction might be done to a tolerance of 1/64^th of an inch while machining of an engine component might be done to a tolerance of 1/10,000^th of an inch. In science, reproducibility is referred to as such or as "the uncertainty." The word "tolerance" is not used in the context of scientific measurement but means the same thing.

·         Stating Results 
The following are some terms that are frequently used in reporting and comparing results: In some experiments, a physical measurement will be made and this "experimental" value will be compared to a value that is widely accepted by other scientists. This accepted value is usually called the "accepted" or "true" value. These values will usually have uncertainties associated with them, but the uncertainty will not always be stated. If it is not stated, it is implied that the last digit is the uncertain digit. For example, if the density of aluminum is given to be 2.698 g/cm³, it is implied that the uncertainty is .001 g/cm³. The experimental value may also be compared with a theoretical or predicted value that is based on hypothesis or theory.

o    Accuracy 
The accuracy of an experiment is the measurement of how close the result is to the accepted or predicted value. Thiscanbestatedinseveralways.

o    Precision 
The Precision is a measurement of how reproducible or how well the result of an experiment is known. The precision of the measurement is referred to as the "uncertainty" and has the same units as the measured value. Theresultofanexperimentwouldbestatedas:

The "uncertainty" can be expressed as an "absolute" uncertainty or a "relative" uncertainty and frequently is seen both ways. For example, suppose the result of a length measurement using a meter stick is 14.7 cm. And, further, suppose that as a result of the way the meterstick was marked, it was possible to estimate that the uncertainty in this value was 0.1 cm, then the result of the measurement would be reported as follows:

The "± 0.1 cm" is the uncertainty in this measurement and it is an "absolute" uncertainty. Often, it is more useful to have the "relative" uncertainty expressed because this states how big the uncertainty is compared to the quantity being measured.

So, in this example, the relative uncertainty is:

Please notice that "precision" and "accuracy" are not the same thing! It is possible to have a very precise measurement that is has a very large "error" because something was wrong with the measuring device or the person using it was not using it properly.

Random uncertainties: An example of something that naturally varies is the number of apples on a tree. Suppose that there is an orchard consisting of dwarf apple trees that are as uniform as possible. Even though every effort is made to have these trees be uniform there will be natural, random variation in the number of apples that will mature on each that can have a basis in anything from pollination to insect infestation. The total number of apples on any tree can be counted exactly, but the number varies from tree to tree. It might be very helpful to have a representative number for the number of apples on a tree in this orchard. What should that number be? In fact, a number is really not the answer; we probably ought to have a range so that we not only know about how many apples to expect per tree but we also have a good measure of just how variable this can be. In-other-words, the answer to the question will be the result as expressed above and again here:

In this example the "measured value" would be the AVERAGE of a number of sample counts. The "uncertainty" is usually given by the "sample standard deviation". This quantity is often represented by a lower case Greek letter sigma, σ_n-1, with the n-1 indicating that this is the "sample" rather than "population" value. When you have a choice with your calculator, use the σ_n-1 function. On TI-8X series calculators this function is represented by "Sx", and "σ" is reserved for the population standard deviation. No attempt will be made here to describe how to compute the sample standard deviation if your calculator will not do it for you. The equation that follows is presented so that there is no confusion about what value is expected in our laboratory work.

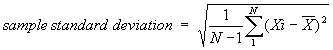
(Where "N" is the number of samples, X_i is a particular sample, "i" represents the position in the list of the results for that sample and X is the average of the individual samples.)

The significance of the standard deviation as a measure of uncertainty is that the range it describes around the average includes a predictable number of the samples. So, for example, if our sample of trees in the orchard gives as a result of our counting and calculation:

The "147" is the average of the number of apples counted on the trees in our sample and the "9" is the sample standard deviation. So the RANGE, 138 → 156, contains 68% of the values used to calculate the average. Another interpretation of this range is that there are 68 chances out of 100 of obtaining a value in this range if one were to count another tree in the orchard. For our purposes in this course, we are going to be a little casual about this 68% and simply refer to this as approximately equivalent to 2/3 or two chances out of three.

If, instead of counting, one is using a tool to make some measurement, then the separate results of repeated measurements are averaged and the sample standard deviation calculated in the same way.

Systematic error: This is the result of the measuring device having a built in error - or - the person using it, not being aware of how to use the device properly. This can be something as simple as forgetting to "tare" (set to zero, usually) the electronic scales or it might be the result of using a cheap ruler on which the inscribed distances are, say, 2.3% too short. These kinds of errors are very hard to detect sometimes. They don't always have an effect on what one is trying to discover, but we often "calibrate" equipment to test for the presence of systematic error, because they can lead to serious problems if undiscovered.

Precision and Accuracy

When taking scientific measurements, the goals are to measure accurately and with precision.

·         Accuracy indicates the closeness of the measurements to the true or accepted value.

·         Precision is the closeness of the results to others obtained in exactly the same way.

In the laboratory, you may be measuring a quantity that has an accepted value. The difference between the measured result and the accepted value is the error in the result.

·         error = measuredvalue - acceptedvalue

·         % error = (error in measurement/accepted value) x 100

For example, the accepted value for the mass of a new golf ball is 45.93 g. A student weighs a golf ball and finds it to be 46.45 g. The % error is:

 % error    = (error in measurement/accepted value) x 100

                 = [(46.45 – 45.93)/45.93] x 100

                 = [0.52/45.93] x 100

                 = 1.13%

It is common practice to take a number of separate measurements. This eliminates any ‘outlier’ results (results that do not fit the expected outcome) and allows for an average value to be taken.

For example, a student weighs a golf ball on five separate occasions, and the results are: 45.89 g, 45.91 g, 46.06 g, 36.98 g and 45.94 g. On looking carefully at the results, it is clear that the result ‘36.98 g’ does not fit in with the other results. It is an ‘outlier’ and is discarded.

The average mass is calculated as:

(45.89 + 45.91 + 46.06 + 45.94)/4 = 45.95 g

Additional problem for differentiation 1: Coin diameter: A gold coin has an ‘accepted’ diameter of 28.054 mm.

Two students measure the diameter of four gold coins. Student A uses a simple plastic ruler. Student B uses a precision measuring tool called a micrometer.

1.      Calculate the average value for each set of measurements

2.      Calculate the % error for each set of measurements.

3.      Compare the average value for each set with the accepted value:

• Which student’s data is more accurate?
• Which student’s data is more precise?

4.      Compare the percentage error for each set:

• Which student’s data is more accurate?
• Which student’s data is more precise?

5.      Explainanyoddfindings:

Additional problem for differentiation 2:Aluminium bar density: The ‘accepted’ density of aluminium is 2.702 g/cm³.) Since density is mass/volume, the students need to calculate the volume of the cylinder. To do this, the height and diameter of the cylinder need to be measured.

Student A is told to use a simple plastic ruler and to make four independent measurements for each dimension. Student B is told to use a precision measuring tool called a micrometer.

1.      Calculate the average value for each set of density values, making sure that any ‘outliers’ are not included.

2.      Calculate the % error for each set of values.

3.      Compare the average value for each set with the accepted value:

• Which student’s data is more accurate?
• Which student’s data is more precise?

4.      Compare the percentage error for each set:

• Which student’s data is more accurate?
• Which student’s data is more precise?

5.      Explainanyoddfindings:

Useful links

https://www.bluffton.edu/homepages/facstaff/bergerd/NSC_111/Measurements.html

Cambridge International A Sand A Level Physics Coursebook

https://www.thoughtco.com/difference-between-accuracy-and-precision-609328

https://www.mathsisfun.com/accuracy-precision.html

https://www.quora.com/What-is-the-difference-between-precision-and-accuracy-in-physics

https://www.youtube.com/watch?v=0IiHPKAvo7g

https://courses.lumenlearning.com/introchem/chapter/accuracy-precision-and-error/

Скачано с www.znanio.ru