PHY_10_3_V2_TG_defining acceleration of a body moving on an inclined plane

Guidance for teacher

To determine the acceleration at any point along the inclined plane, you will place the cart at the bottom of the ramp, gently nudge the cart such that when released, it will move up the ramp, momentarily stop, and begin moving down the inclined plane. Carts moving in gravity fields will experience variable motion which can be observed by an ultrasonic motion sensor. If position and velocity graphs are created using PASCO Capstone, where the slope of the position vs. time graph represents the velocity of the cart and the slope of the velocity vs. time graph represents the acceleration. You will use your knowledge of motion graphs to observe the nature of acceleration as the cart moves up the ramp, momentarily stops, and then moves down the ramp.

3. Friction: force or coefficient? Everyday life gives many sensory experiences of friction in action, showing clearly the importance of what surfaces are involved. Anyone trying to move something across a floor knows that a harder push is needed to move a heavier object. By pressing objects together, we may sometimes prevent slipping. With standard physics notation we may note that the frictional force, F, can be expressed as F≤ µN, in terms of the normal force, N, and the coefficient of friction, µ, where the equality holds when objects are moving /1/. The inequality for static friction implies that a body remains at rest on an inclined plane as long as the angle is sufficiently small. The inequality used to express static friction often causes difficulties in traditional physics problem solving: The size and direction of the static friction force cannot be determined without knowing the other relevant forces for a given situation. An inclined plane with a slope θ exerts a normal force N=mg cos θ on a body with mass m. If the body is at rest (or moving with constant speed), the upward friction force must be F= mg sin θ to counteract the tangential component of the force of gravity. This leads to the condition for the slope: tan θ ≤ µ. For a slope with angle of inclination θ! where a body starts sliding, or slides with constant speed, the force s of friction exactly opposes the force of gravity along the plane, and we can measure the coefficient of friction as µ = tan θ = h/b, where h and b are the corresponding vertical and horizontal distances, as shown in Figure 4. Although the equations and definitions are unlikely to be accessible to young learners, the relations have some remarkable and counterintuitive consequences that can be appreciated and investigated much earlier, as discussed below. A first observation is that the surface area does not enter the expression for the friction force. A second observation is that the slope at which a body starts to slide is independent of the mass. Since the frictional force, like gravity and inertia, is proportional to the mass of a sliding object, all terms in the equation of motion for the body on an inclined plane are proportional to the mass. Thus, the mass should not affect how fast an object slides down a plane. This knowledge helps the teacher provide scaffolding for the investigations and discussions.

1. THEORETICAL MATERIALS FOR LESSON:

Working with Inclined Planes

We discussed previously that when an object rests on a horizontal surface, there is a normal force supporting it equal in magnitude to its weight. Up until now, we dealt only with normal force in one dimension, with gravity and normal force acting perpendicular to the surface in opposing directions (gravity downward, and normal force upward). Now that you have the skills to work with forces in two dimensions, we can explore what happens to weight and the normal force on a tilted surface such as an inclined plane. For inclined plane problems, it is easier breaking down the forces into their components if we rotate the coordinate system, as illustrated in Figure 1. The first step when setting up the problem is to break down the force of weight into components.

Figure 1The diagram shows perpendicular and horizontal components of weight on an inclined plane.

When an object rests on an incline that makes an anglewith the horizontal, the force of gravity acting on the object is divided into two components: A force acting perpendicular to the plane,, and a force acting parallel to the plane,. The perpendicular force of weight,, is typically equal in magnitude and opposite in direction to the normal force,The force acting parallel to the plane,, causes the object to accelerate down the incline. The force of friction,, opposes the motion of the object, so it acts upward along the plane.

It is important to be careful when resolving the weight of the object into components. If the angle of the incline is at an angleto the horizontal, then the magnitudes of the weight components are

Instead of memorizing these equations, it is helpful to be able to determine them from reason. To do this, draw the right triangle formed by the three weight vectors. Notice that the angle of the incline is the same as the angle formed betweenand. Knowing this property, you can use trigonometry to determine the magnitude of the weight components

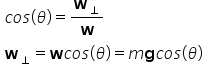
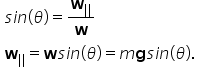
To review, the process for solving inclined plane problems is as follows:

1.      Draw a sketch of the problem.

2.      Identify known and unknown quantities, and identify the system of interest.

3.      Draw a free-body diagram (which is a sketch showing all of the forces acting on an object) with the coordinate system rotated at the same angle as the inclined plane. Resolve the vectors into horizontal and vertical components and draw them on the free-body diagram.

4.      Write Newton’s second law in the horizontal and vertical directions and add the forces acting on the object. If the object does not accelerate in a particular direction (for example, the x -direction) then Fnet x = 0. If the object does accelerate in that direction, Fnet x = ma.

5.      Check your answer. Is the answer reasonable? Aretheunitscorrect?

FINDING THE COEFFICIENT OF KINETIC FRICTION ON AN INCLINED PLANE

A skier, illustratedin Figure 5.37(a), with a massof 62 kgisslidingdown a snowyslopeatanangleof 25 degrees. Findthecoefficientofkineticfrictionfortheskieriffrictionisknowntobe 45.0 N.

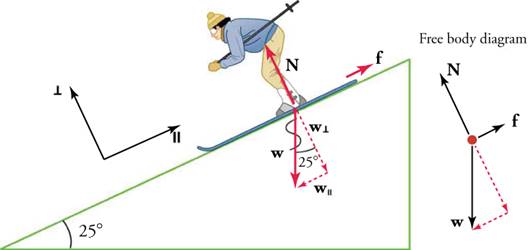
Figure 5.37 Usethediagramtohelpfindthecoefficientofkineticfrictionfortheskier.

Strategy

Themagnitudeofkineticfrictionwasgivenas 45.0 N. Kineticfrictionisrelatedtothenormalforce Nas .Therefore, wecanfindthecoefficientofkineticfrictionbyfirstfindingthenormalforceoftheskieron a slope. Thenormalforceisalwaysperpendiculartothesurface, andsincethereisnomotionperpendiculartothesurface, thenormalforceshouldequalthecomponentoftheskier’sweightperpendiculartotheslope.

Thatis,

Substitutingthisintoourexpressionforkineticfriction, weget

whichcannowbesolvedforthecoefficientofkineticfriction μk.

SOLUTION

Solvingforgives

Substitutingknownvaluesontheright-handsideoftheequation,

DISCUSSION

Thisresultis a littlesmallerthanthecoefficientlistedinTable 5.1 forwaxedwoodonsnow, butitisstillreasonablesincevaluesofthecoefficientsoffrictioncanvarygreatly. Insituationslikethis, whereanobjectofmass m slidesdown a slopethatmakesanangle θ withthehorizontal, frictionisgivenby

FRICTION AT AN ANGLE: SLIDING A COIN

Anobjectwillslidedownaninclinedplaneat a constantvelocityifthenetforceontheobjectiszero. Wecanusethisfacttomeasurethecoefficientofkineticfrictionbetweentwoobjects. Asshowninthefirst WorkedExample, thekineticfrictionon a slope, andthecomponentoftheweightdowntheslopeisequalto. Theseforcesactinoppositedirections, sowhentheyhaveequalmagnitude, theaccelerationiszero. Writingtheseout

Solvingfor, sincewefindthat

5.10

Materials:

1 coin

1 book

1 protractor

Put a coinflaton a bookandtiltituntilthecoinslidesat a constantvelocitydownthebook. Youmightneedtotapthebooklightlytogetthecointomove.

Measuretheangleoftiltrelativetothehorizontalandfind.

GraspCheck

TrueorFalse—Ifonlytheanglesoftwovectorsareknown, wecanfindtheangleoftheirresultantadditionvector.

True

False

Useful links

https://www.youtube.com/watch?v=Scp08vzaacs

DOUGLAS C. GIANCOLI, Physics principles with applications

Скачано с www.znanio.ru