План конпект

ГКОУ РД «Карабудахкентская специальная (коррекционная) общеобразовательная школа – интернат

 

      ОТРКРЫТЫЙ УРОК

                         ПО ТЕМЕ

«ТЕОРЕМА ПИФАГОРА»

                                     8 КЛАСС

17.11.2019 г.

Класс: 8

Учебный предмет: геометрия

Автор УМК: Геометрия. Учебник для 7 – 9 классов. Погорелов А.В. 2-е изд. - М.: Просвещение, 2014 - 240 с

Тема урока (учебного занятия): «Теорема Пифагора»

Задачи урока:

Общеобразовательные:

1.                  Изучить теорему Пифагора, доказательство теоремы Пифагора, исторические сведения о Пифагоре и его теореме;

2.                  Проверить способность к творческому мышлению и самостоятельной деятельности;

3.                  Научить применять полученные знания на практике (применение теоремы Пифагора при решении задач, практическое применение теоремы Пифагора, ее значение);

4.                  Активизировать познавательную активность.

Воспитательные:

1.                  Вовлечь в активную деятельность;

2.                  Совершенствовать навыки общения со взрослыми и сверстниками;

3.                  Воспитывать умение слушать, анализировать, соблюдать единые требования к оформлению решений;

4.                  Содействовать формированию познавательного интереса к математике.

Развивающие:

1.                  Совершенствовать навыки анализа;

2.                  Развивать коммуникативные навыки работы в парах;

3.                  Умение формулировать выводы;

4.                  Развивать память и математический кругозор;

5.                  Продолжить развитие умения устанавливать причинно-следственные связи;

6.                  Способствовать развитию представлений обучающихся об особенностях заданий по данной теме.

Планируемые результаты:

Личностные:

1.                  Способность к эмоциональному восприятию математических объектов, задач, решений, рассуждений

2.                  Представление о математической науке как сфере человеческой деятельности, об этапах ее развития, о ее значимости для развития цивилизации

3.                  Креативность мышления, инициатива, находчивость, активность при решении математических задач

Метапредметные:

1.                  Способность сознательно организовывать и регулировать свою деятельность — учебную, общественную и др.

2.                  Владение умениями работать с учебной и внешкольной информацией (анализировать и обобщать факты, составлять простой и развернутый план, тезисы, формулировать и обосновывать выводы и т. д.)

3.                  Готовность к сотрудничеству с соучениками, коллективной работе, освоение основ межкультурного взаимодействия в школе и социальном окружении

4.                  Умение видеть математическую задачу в контексте проблемной ситуации в других дисциплинах

5.                  Умение самостоятельно ставить цели, выбирать и создавать алгоритмы для решения учебных математических проблем

Предметные:

1.      Овладение базовым понятийным аппаратом по основным разделам содержания

2.      Овладение геометрическим языком, умение использовать его для описания предметов окружающего мира

3.      Использовать формулы для нахождения сторон прямоугольного треугольника

4.      Умение применять изученные понятия, результаты, методы для решения задач практического характера

5.      Проводить доказательства теоремы Пифагора.

Формы деятельности: индивидуальная, парная, фронтальная.

Ресурсы: презентация, компьютер, мультимедийный проектор, экран

Тип урока: урок открытия новых знаний

Цель урока: рассмотреть теорему Пифагора и доказательство теоремы, показать её применение при решении задач.

Ход урока:

 

1. Организационный момент

2.Актуализация знаний (Слайд 1)

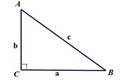
1)Как называется фигура, изображенная на рис.? (Прямоугольный треугольник)

2)Какой треугольник называется прямоугольным? (Это треугольник, в котором один угол прямой (то есть 90 градусов))

3)Как называются его стороны? (Катет и гипотенуза)

4)Что такое гипотенуза? (Сторона прямоугольного треугольника, противоположная прямому углу)

5)Что такое катет? (Одна из двух сторон прямоугольного треугольника, образующих прямой угол)

6)Назовите по рисунку гипотенузу и катет. (Катеты АС и ВС; гипотенуза АС) 

7)Что такое косинус угла прямоугольного треугольника? (Отношение прилежащего катета к гипотенузе)

8)В прямоугольном треугольнике АВС катет АС равен 7 см,  а гипотенуза АB равна 25 см. Найдите косинус угла А и катет ВС.

Решение:  =  =  см

Учитель: А как же найти неизвестную сторону в прямоугольном треугольнике, зная  две другие его стороны. На сегодняшнем уроке мы с вами с этим  познакомимся и обратимся к данной задаче в конце урока.

3. Практическая работа. Проведение эксперимента. (Слайд 2)

Учитель: Ребята, следующим этапом нашего урока будет практическая работа, в ходе которой мы проведем эксперимент по определению длин сторон прямоугольного треугольника и выяснения связей между ними. Работа в тетрадях.

План практической работы:

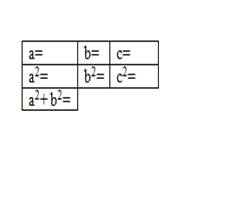1. Изобразите в тетради прямоугольный треугольник с катетами a, b и гипотенузой c. (длины сторон треугольника определите целыми числами).

2. Измерьте катеты a, b и гипотенузу c. Результаты запишите в таблицу.

3. Найдите квадраты полученных величин a, b и c. Результаты запишите в таблицу.

4. Найдите сумму a² + b². Результат запишите в таблицу.

5. Сравните полученный результат с квадратом гипотенузы c².

6. Сделайте вывод.

Учащаяся: У меня получилось, что выражения с² и (a² + b²) равны между собой (Например:5²=3²+4², 25=25).

Учитель: А выражение с²– это что за выражение?

Учащиеся: Это квадрат гипотенузы.

Учитель: А что собой представляет выражение a²+b²?

Учащиеся: Это сумма квадратов двух катетов.

Учитель: Правильно. Так какой же вывод напрашивается?

Учащиеся: Квадрат гипотенузы равен сумме квадратов катетов.

Учитель: Совершенно верно. Мы с вами, ребята, практическим путем установили, что в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов. Так звучит знаменитая теорема Пифагора, она из главных теорем геометрии. Запишем в тетрадях тему урока: «Теорема Пифагора». (Слайд 3)

 

4.Изучение теоремы.

Учитель: Как вы знаете, у каждой теоремы, есть доказательство. Сейчас мы попробуем с вами одним из способов её доказать. Откройте учебники на странице 85. Прочитайте доказательство теоремы и попробуйте доказать её самостоятельно. Сначала попробуйте объяснить доказательство теоремы соседу по парте. Затем один из вас выйдет к доске и объяснит доказательство теоремы  перед всем классом на оценку. (Слайд 4)

Теорема Пифагора: В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов, т.е. a²+b² = с²

Доказательство:

 

Дано: ∆АВС-прямоугольный треугольник,  С = 90°, а, b – катеты, с – гипотенуза.

Доказать: с² = а² + b².

Доказательство: Проведем высоту СD из вершины прямого угла С.

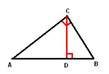
 По определению косинуса угла:  =  = . Отсюда АВ  АD = АС²

Аналогично,  =  = . Отсюда АВ  ВD = ВС²

Складывая полученные равенства почленно и замечая, что АD + DВ = АВ, получим:

АС² + ВС² = АВ (АD + DВ) = АВ² или с² = а² + b²   Теорема доказана.

 

          Доказательство этого факта принадлежит древнегреческому ученому Пифагору (Vlв. до н.э.), о жизни которого и истории открытия теоремы мы узнаем в следующем видеоролике. (Слайд 5)

 

5. Закрепление изученного материала.

Для каждой из задач на доске один из учеников выполняет чертеж, объясняет и кратко записывает решение задачи. Остальные ребята работают в тетрадях.

1) Решение задач по готовым чертежам (Слайд 6)

Задача 1

 

Дано: АВСD – четырехугольник.

           СD=8см; ВD=17 см.

Найти: AD

 

 

Решение:

Из прямоугольного треугольника BCD можно найти сторону ВС. По теореме Пифагора:

ВС² = ВD² - CD². Отсюда ВС² = 17² - 8² = 289 – 64 = 225. Отсюда ВС = 15 см.

Так как в четырехугольнике противоположные стороны равны, то ВС =  AD = 15 см.

Ответ: AD=15 см.

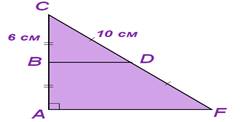
Задача 2

 

Дано: ∆АCF-прямоугольный треугольник

           AB=BC, СD=DF; ВD‖‖AF

           BC=6см; CD=10 см.

Найти: BD, AF

 

Решение:

 

Из прямоугольного треугольника BCD можно найти сторону ВD. По теореме Пифагора:

ВD² = CD² - BC². Отсюда ВD² = 10² - 6² = 100 – 36 = 64. Отсюда ВD = 8 см.

Из прямоугольного треугольника ACF можно найти сторону AF. По теореме Пифагора:

AF² = CF² - AC². Так как  CF =2 CD  и AC=2 BC, то    AF² = (2² - (2² = 400 – 144 = 256. Отсюда AF = 16 см.

Ответ: BD=8 см, AF=16 см.

 

2)Старинная задача (Слайд 7).

 

 Учитель: Следующая задача  взята из первого учебника математики на Руси. Называется этот учебник “Арифметика”.

Случися некому человеку к стене лестницу прибрати, стены же тоя высота 117 стоп. И обрете он лестницу долготою 125 стоп. И ведати хочет, колико стоп сея лестницы нижний конец от стены отстояти имать.

 

 

 

 

Дано: ∆АBC-прямоугольный треугольник, С = 90°

           AC=117стоп, AB=125 стоп.

Найти: CB

Решение

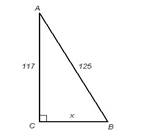
Так как  ∆АBC прямоугольный, то по теореме Пифагора: CB² = AB² - AC². Отсюда CB² = 125² - 117² =(125-117)(125+117) =  1936. Отсюда CB = 44 стопы.

Ответ: 44 стопы

 

 

6. Тест

1. К каким треугольникам можно применить теорему Пифагора?

1.                  К любым;

2.                  К равносторонним

3.                  К равнобедренным;

4.                  К прямоугольным;

Ответ:4

2.В прямоугольном треугольнике квадрат гипотенузы равен…

1.                  сумме катетов;

2.                  квадрату катета;

3.                  сумме квадратов катетов;

4.                  произведению  двух катетов

Ответ: 3

3.Гипотенуза прямоугольного треугольника равна 13 см, катет 5 см. Найти длину второго катета.

1.                  12 см;

2.                  13 см;

3.                  14 см;

4.                  15 см.

Ответ: 1

4.Чему равна гипотенуза прямоугольного треугольника, катеты которого равны 9 см и 40 см?

1.                  35 см;

2.                  39 см;

3.                  41 см;

4.                  44 см.

Ответ: 3

 

5. В равнобедренном треугольнике АВС ВН - биссектриса. АВ = 17 см, ВН = 15 см. Найдите АС.

1.                  4 см;

2.                  8 см;

3.                  16 см;

4.                  24 см.

Ответ: 3

 

7. Подведение итога урока.

Учитель: Ребята, давайте вспомним, с какой задачи мы с вами начали наш урок: как же найти неизвестную сторону в прямоугольном треугольнике, зная  две другие его стороны?

Обучающиеся систематизируют и обобщают полученные знания, делают выводы и приходят к общему решению задачи.

8. Рефлексия

- Оцените свою работу. Выставите фигурку, которая покажет уровень понимания, того чем мы занимались на сегодняшнем уроке. Начертите отрезок, на одном конце 0 (ничего не понятно) на другом 1 (всё понятно).

 

                                                  

       

9.      Домашнее задание:

№5, 7

 

Директор  ГКОУ РД  «КСКОШИ»            Гаджиева И.С.

ГКОУ РД «Карабудахкентская специальная (коррекционная) общеобразовательная школа – интернат

 Отзыв об уроке, проведённом учителем математики Кахрумановой Зульфии Гасановны     об уроке  геометрии  в 8  классе по теме

 «ТЕОРЕМА ПИФАГОРА»

Цели занятия, его план, представленные  обучающимся, были конкретными и побудительными. Замысел занятия реализован. Содержание занятия  оптимально, доступно. Проблемный характер изложения учебного материала. Обучающиеся имели возможность выбора форм и средств работы, вариантов представления результатов. Были созданы условия для актуализации опыта обучающихся, их личностного общения.

Занятие способствовало формированию ключевых компетенций:                                                  в предметной области; в области информационных технологий; в плане продолжения образования и  эффективного самообразования.

Занятие способствовало  развитию  качеств личности:

коммуникативность, способность к эффективному общению.

критическое мышление

креативность, установка на творчество

самостоятельность и ответственность

рефлексивность, способность к самооценке и самоанализу

толерантность, уважение к межкультурным и прочим различиям

Обучающиеся получили помощь в решении значимых для них проблем

Педагог сумел заинтересовать обучающихся, владел классом.

Комфортность образовательной среды: материально-техническое  обеспечение, удобство расстановки рабочих мест.

Качество методического обеспечения (пособия, раздаточные материалы, материалы на электронных носителях и пр.) методы обучения и контроля адекватны возможностям обучающихся.

Психологическая комфортность: благоприятный климат (доброжелательность, личностно-гуманное отношение к обучающимся).

Директор  ГКОУ РД  «КСКОШИ»            Гаджиева И.С.