План – конспект урока по элективному курсу в 11 классе по теме «Производная на ЕГЭ по математике»

План – конспект урока по элективному курсу в 11 классе по теме «Производная на ЕГЭ по математике»

                                                             Семенова Секинат Магомедовна, учитель математики

                                                                                   МКОУ « СОШ № 2  г.Усть-Джегуты»

      «…нет ни одной области в математике, которая когда-либо не окажется применимой к

явлениям действительного мира…»

Н.И. Лобачевский.

Цели урока :

Образовательные :

-уметь применять знания по теме «Производная» при решении заданий из материалов КИМ ов ФИПИ

Развивающие :

- продолжить формирование мыслительных операций; развитие умения учащихся опираться на предыдущие знания, а именно-на правила дифференцирования, формулы производных

Воспитательные :

-продолжить воспитание отношения к математике как к жизненной науке; воспитывать познавательную активность учащихся

Оборудование : ПК, проектор, экран

Ресурсный материал  :

-ЕГЭ. Задания профильного  уровня  № 8,14

-ЕГЭ. Математика  . Модульный курс « Я сдам ЕГЭ». Профильный уровень. Рабочая тетрадь.

Тип урока: комбинированный

Методы обучения:  объяснительно-иллюстративный, репродуктивный.

                                                         Ход урока :

I.Оргмомент

II.Актуализация знаний ( Слайды  1-2)

1.Повторяем правила дифференцирования

2. В чем состоит геометрический смысл производной?

3.В чем состоит физический смысл производной?

4.Написать  формулы дифференцирования.

5.Написать уравнения касательной.

6 .Какие точки называются критическими?

( Внутренние точки области определения функции, в которых ее производная равна нулю или не существует, называются критическими точками этой функции.)

7.В чем состоит необходимое условие экстремума?

 ( Если точка  х₀ является точкой экстремума функции f  и в этой точке существует

                        производная  f '(x), то она равна нулю: f '(x)= 0)

8.В чем состоит достаточный признак существования экстремума?

( Признак  максимума. Если функция f непрерывна в точке х₀, a f '(x) 0 на интервале (а; х₀) и f '(x)= (x)0 на интервале (х_о; в), то точка х_о является точкой максимума функции f.

Удобно пользоваться упрощенной формулировкой этого признака: если в точке х₀ производная меняет знак с плюса на минус, то хо - есть точка максимума.

Признак минимума функции. Если функция f непрерывна в точке х_о, а f '(x)<0 на интервале

(а; х_о) и f '(x)>0 на интервале (х₀; в), то точка х₀ является точкой минимума функции f. (Если в точке х₀ производная меняет знак с минуса на плюс, то х₀ есть точка минимума функции f).

9.Алгоритм отыскания наибольшего и наименьшего значений функции у= f(x), непрерывной на отрезке [a; b].

1.Найти f '(x)

2.Найти критические точки, т.е. где f '(x) =0 и f '(x) не существует, и отобрать из них те, что лежат внутри отрезка [a; b].

3.Вычислить значения функции y= f(x) в критических точках и на концах отрезка, и выбрать из них наибольшее и наименьшее; они и будут соответственно наибольшим и наименьшим значениями функции y=f(x) на отрезке [a; b], которые обозначают так: max _{[a; b]} y(x) и

min _[a;b]y(x).

III.Выполнение упражнений ( Слайды 3-15)

1. На рисунке изображён график функции y=f(x). На оси абсцисс отмечены шесть точек: x₁, x₂, x₃, x₄, x₅, x₆. В скольких из этих точек производная функции f(x) отрицательна?

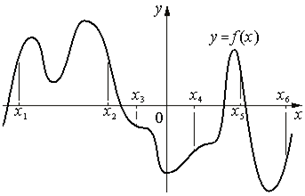
2.На рисунке изображён график функции y=f(x). На оси абсцисс отмечены семь точек: x₁, x₂, x₃, x₄, x₅, x_6, х ₇. . В скольких из этих точек производная функции f(x) положительна?

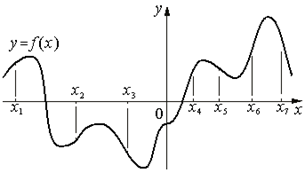
3.На рисунке изображены график функции y=f(x) и касательная к нему в точке с абсциссой x₀. Найдите значение производной функции f(x) в точке x₀.

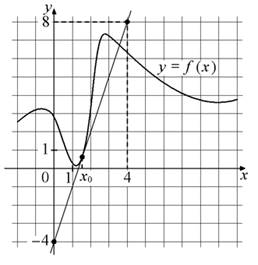
4.Найдите наименьшее значение функции y=x³−x²−8x+4 на отрезке [1; 7]

5.На рисунке изображён график y=f′(x) — производной функции f(x), определённой на интервале (−9; 8). Найдите точку экстремума функции f(x) на отрезке [−3; 3].

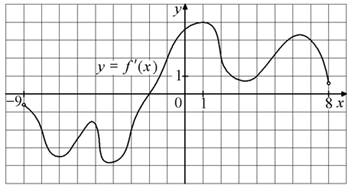
6.На рисунке изображён график функции y=f(x), определённой на интервале (− 9; 5). Найдите количество точек, в которых производная функции f(x) равна 0.

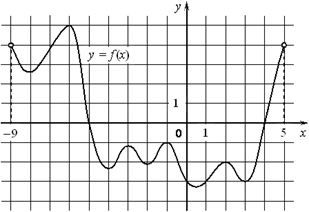
7.На рисунке изображён график y=f′(x) производной функции f(x), определённой на интервале (− 2; 9). В какой точке отрезка [2; 8] функция f(x) принимает наименьшее значение?

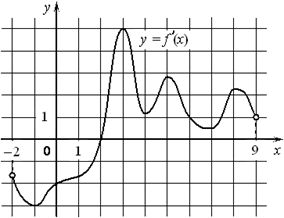
8.На рисунке изображён график y=f '(x) — производной функции f(x), определённой на интервале (− 11 ; 6). Найдите количество точек минимума функции f(x), принадлежащих отрезку [− 6 ; 4].

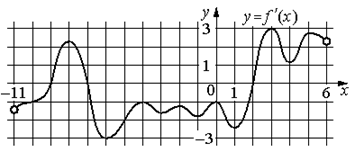
9.На рисунке изображён график функции y=f(x), определённой на интервале (− 6 ; 6). Найдите количество решений уравнения f '(x)=0 на отрезке [− 4,5 ; 2,5].

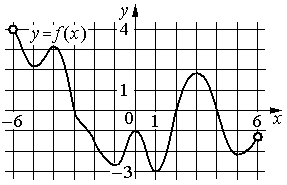
10.Материальная точка движется прямолинейно по закону x(t)=16 t³−2 t²+6 t+250, где x — расстояние от точки отсчёта в метрах, t — время в секундах, измеренное с момента начала движения. В какой момент времени (в секундах) её скорость была равна 96 м/с?

11. Найдите силу F , действующую на материальную точку с массой m , движущуюся прямолинейно по закону х ( t ) =5 t ³ - 4t ²  ,при t = 5.

12. При извержении вулкана магма своим поведением напоминает дрожжевое тесто: она увеличивается в объёме и занимает абсолютно всю свободную территорию, до которой только может добраться, поднимаясь из недр нашей планеты по всем доступным ей трещинам. Добравшись до наименее плотно закупоренных мест, под влиянием содержащихся в ней газов, что пытаются любым способом её покинуть (процесс этот называется дегазация магмы), она пробивает земную кору и, выбив «пробку» вулкана, вырывается наружу. После того как магма вышибает пробку вулкана, давление в магматическом очаге (его верхней части) моментально понижается. Пусть движение этой « пробки» описывается законом : р(t) = t²- 5 t+12, где t- время в секундах. В какой момент времени (в секундах) скорость движения «пробки» вулкана  будет равна 15 м/с?

13. Популяцией в экологии называют группу особей одного вида, находящихся во взаимодействии между собой и совместно населяющих общую территорию. Слово «популяция» происходит от латинского «популюс» – народ, население. Экологическую популяцию, таким образом, можно определить как население одного вида на определенной территории. Скорость роста популяции — изменение численности популяции за единицу времени.

Задача :

Зависимость численности популяции тигров задана формулой N(t)= 5 t³-4 t²+1. Найдите прирост популяции в момент времени t = 3.

IV.Самостоятельная работа

Теперь поработаем самостоятельно в рабочих тетрадях модульного курса «Я сдам ЕГЭ»

С.163 ,№ 6,7,8,9

С.174, № 5,6

С.193 , №1,2

С.198, № 1,2

(1 вариант- четные номера, 2 вариант – нечетные)

В работе 5 заданий, каждое задание в отдельности составляет 20 %.

Критерий оценивания :

V.  Подведение  итогов. Рефлексия.

Урок хотелось бы закончить словами Крылова Алексея Николаевича ,советского математика и кораблестроителя: «Теория без практики мертва или бесполезна, практика без теории невозможна или пагубна».

VI.Домашнее  задание :  Модульный курс .Я сдам ЕГЭ.(профильный уровень) ,

   с.193-№ 3,4;

 с.198-№3-5;

с.202-№ 1,2.