
Публикация является частью публикации:
ПЛАН УРОКА
Тема: Повторение решений логарифмических уравнений
По предмету: Математика
Разработала:
учитель математики Кобелева Н.В.
План урока
Предмет: Математика
Класс:
Тема урока: Повторение по теме: «Решение логарифмических уравнений»
Тип урока: Уроки совершенствования знаний, умений и навыков
Время урока: 40 минут
Цели урока
1) Закрепить умения применять эти понятия при решении уравнений.
2) Формировать умения решать задачи, используя тесты.
3) Создавать атмосферу заинтересованности каждого учащегося в работе группы.
Оснащение урока: ПК, проектор, экран, доска, мел.
Программное обеспечение: электронный учебник «Математика, часть I», опорные конспекты, карточки для самостоятельного решения, презентация.
Межпредметные связи: Информатика: Создание презентации;
Применение электронного учебника
«Математика, часть I».
Литература: Развитие грамотной речи.
Ход урока
|
Время |
Структурное построение урока |
Задачи |
МТО урока |
Межпредметные связи |
Деятельность |
|
|
Учителя |
Обучающихся |
|||||
|
2 мин. |
Организационный момент |
Общение с обучающимися, создание атмосферы заинтересованности |
Опорные конспекты, канцелярские принадлежности |
|
1.Приветствие обучающихся 2. Объявление темы урока, основных целей и хода урока (слайды 1, 2) |
1. Сидят на своих местах. 2. Записывают дату и тему урока: «Повторение решений логарифмических уравнений» |
|
5 мин. |
Повторение и обобщение знаний по теме: «Логарифмическая функция и её свойства» |
Повторить определение логарифмической функции, закрепить умение строить график логарифмической функции и определять свойства данной функции с помощью индивидуального опроса обучающегося. |
Доска, мел, карточка |
|
Приглашает 1 обучающегося к доске и просит выполнить задание по карточке на повторение по теме «Логарифмическая функция и её свойства» с последующим объяснением: Карточка: 1) какая функция называется логарифмической;
2) построить график функции у = log2х и перечислить её свойства.
Дополнительный вопрос: Когда логарифмическая функция убывает? |
Определение: Функцию, заданную формулой у = logах, называют логарифмической функцией с основанием а.
Свойства: 1) Д(у) = (0; +∞) 2) Е(у) = R 3) Логарифмическая функция на все области определения возрастает (при а>1).
Убывает, когда основание больше 0, но меньше 1. |
|
Время |
Структурное построение урока |
Задачи |
МТО урока |
Межпредметные связи |
Деятельность |
|
|
Учителя |
Обучающихся |
|||||
|
|
Повторение и обобщение знаний по теме: «Умение области определения и умение решать показательные уравнения» |
Применение знаний обучающихся по данным темам. |
Индивидуальные карточки, канцелярские принадлежности.
|
|
Преподаватель предлагает 2 обучающимся решить зада-ния на местах по карточкам на повторение и закрепление по темам «Область определения, решение показательных уравнений и использовании свойств показательных уравнений».
Карточка 1: 1) Найдите область определения функции у=log5(2х-1);
2) Решите уравнение: 4х+1+4х=320
Карточка 2: 1) Найдите область определения функции у=√2х-16
|
2 обучающихся решают по карточкам на местах за то же время, отведенное на повторение.
Ответы обучающегося: 2х-1>0 2х>1 х>1/2 Ответ: (1/2;+∞)
4х+1+4х=320 4х ∙4+4х=320 4х(4+1)=320 4х ∙5=320 4х=320:5 4х=64 4х=43 х=3 Ответ: х=3
Ответы обучающегося: 2х-16≥0 2х≥16 2х≥24 Т.к. в показательной функции у=2х основание больше 1, то функция возрастает. Имеем: х≥4 Ответ: [4;+∞) |
|
Время |
Структурное построение урока |
Задачи |
МТО урока |
Межпредметные связи |
Деятельность |
|
|
Учителя |
Обучающихся |
|||||
|
|
|
|
|
|
2) Решите уравнение: |
32х+3 = (243)-1 32х+3 = (35)-1 2х = - 8 2х+3 = - 5 х = - 4 Ответ: х = - 4 |
|
Выполняется совместно с карточкой у доски (за то же самое время) |
Устная работа |
Развивать умение высказывать своё мнение. Заинтересовать каждого обучающегося занимательными задачами
|
конспект учителя |
|
1 Рассуждалки: 1. а) Это такая штука, в которой что-то не знаешь, а потом вдруг узнаешь, если захочешь это сделать – и сделаешь (слайд 3). б) Иногда задачи решаются только с его помощью (слайд 4). в) Не знаю, есть ли у него листья и стебли, но корни у него есть. Может 1, а может больше. И только у некоторых нет и корней (слайд 5). г) Во 2-м классе они – простые, в 7-м – линейные, в 8-м – квадратные, а в 11-м – логарифмические (слайд 6). 2. а) Некоторым хочется, чтобы он скорее закончился, и они были свободны (слайд 7). б) Кто-то их любит, а кто-то нет, потому что на них надо много думать головой, писать, решить, отвечать (слайд 8). в) На нем говорят, что неправильно решил задачу |
Выполняется совместно с карточкой у доски.
Ответ обучающихся:
Уравнения
Ответ обучающихся:
Урок математики |
|
Время |
Структурное построение урока |
Задачи |
МТО урока |
Межпредметные связи |
Деятельность |
|
|
Учителя |
Обучающихся |
|||||
|
|
|
|
|
|
или примеры (слайд 9). г) А может времени не хватило, ведь он всего 45 мин (слайд 10). |
|
|
|
|
С помощью слайдов развивать логической мышление обучающихся |
ПК, проектор, экран, слайды |
Информатика |
Ребусы: (слайды № 11, 12)
|
Разгадывают ребусы по слайдам № 11, 12: 1. Геометрия
2. Уравнение
3. Показатель
4. Диагональ |
|
|
|
|
|
|
* 3. Загадалки: 1) Французский математик, известна его теорема про корни квадратного уравнения 2) Кто из великих русских писателей занимался составлением арифметических задач? |
Ответ обучающихся: 1) Виет
2) Толстой |
|
3 мин. |
Повторение и обобщение знаний по теме: «Логарифмическая функция и её свойства» |
Напомнить обучающимся определение логарифмической функции и её свойств с помощью подготовленного ответа учащегося. |
Доска, указка |
Литература |
Заслушать человека, работавшего у доски, собрать карточки: Карточка: 1) какая функция называется логарифмической;
|
Человек, работавший у доски, отвечает на вопросы карточки: Определение: Функцию, заданную формулой у=logах, называют логарифмической функцией с основанием а. |
|
Время |
Структурное построение урока |
Задачи |
МТО урока |
Межпредметные связи |
Деятельность |
|
|
Учителя |
Обучающихся |
|||||
|
|
|
|
|
|
2) построить график функции у = log2х и перечислить её свойства.
Дополнительный вопрос: При каком условии логарифмическая функция убывает?
|
Свойства: 1) Д(у) = (0; +∞) 2) Е(у) = R Логарифмическая функция на все области определения возрастает (при а>1).
Убывает, когда основание больше 0, но меньше 1.
Решавшие на местах сдают карточки на проверку. |
|
15 мин. |
Повторение решений логарифмических уравнений |
Напомнить обучающимся, как решаются логарифмические уравнения. |
ПК, проектор и программа «Математика, часть I»
ПК, проектор, слайды |
Информатика
Информатика – математика – литература |
- Теперь переходим к теме нашего урока «Повторение решений логарифмических уравнений». Чтобы напомнить вам как решаются логарифмические уравнения, попрошу посмотреть на экран. - Как уже было сказано, такие уравнения решаются по определению логарифма. Итак, на экране мы видим определение логарифма. Кто нам его прочитает? (слайд № 13)
|
Обучающиеся слушают объяснения с экрана.
Обучающиеся смотрят на экран (слайд № 13) и один из учеников зачитывает определение логарифма: Определение: Логарифмом положительного числа х по основанию а (а>0, а≠1) называется показатель степени, в которую нужно возвести число а, чтобы получить число х. |
|
Время |
Структурное построение урока |
Задачи |
МТО урока |
Межпредметные связи |
Деятельность |
|
|
Учителя |
Обучающихся |
|||||
|
|
|
|
ПК, проектор, слайды
Доска, мел, тетради, канцелярские принадлежности, опорный конспект |
|
Преподаватель переключает на слайд № 14, где приведён пример решения логарифмического уравнения и, рассмотрев пример, устно со всей группой решает уравнения.
- Сейчас мы переходим к повторению. Первый пример из конспекта прорешаю я, чтобы еще раз напомнить алгоритм решения логарифмических уравнений по определению, а остальные - по желанию.
- Теперь я предлагаю вам решить второе уравнение и приглашаю к доске (Ф.И. обучающегося) log4(5х+8)=3
- Следующие уравнение. К доске, пожалуйста, (Ф.И. обучающегося) |
Обучающиеся, рассмотрев пример на слайде № 14, решают устно предложенные примеры. (Ответы проверяют с помощью ПК)
Обучающиеся решают уравнение совместно с преподавателем.
1 обучающийся решает у доски с объяснением, остальные записывают в тетради. log4(5х+8)=3 ОДЗ: 5х+8>0 5х>-8 х>-8:5 х>-1,6 По опред-ю логарифма: 5х+8=43 5х+8=64 5х=64-8 5х=56 х=56:5 х=11,2 € ОДЗ Ответ: 11,2
|
|
Время |
Структурное построение урока |
Задачи |
МТО урока |
Межпредметные связи |
Деятельность |
|
|
Учителя |
Обучающихся |
|||||
|
|
|
|
|
|
log2(х2+4х-3)=1
|
log2(х2+4х-3)=1 ОДЗ: х2+4х-3>0 По опред-ю логарифма х2+4х-3=2 х2+4х-5=0 по теореме Виета: х1+х2 = - 4 х1 = - 5 х1∙х2 = - 5 х2 = 1 Проверка: х1 = -5 € ОДЗ log2((-5)2+4∙(-5)-3) = = log2(25-20-3) = log22 = 2 х1 = 1 € ОДЗ log2(12+4∙1-3)=log2(1+4-3) = = log22 = 2 Ответ: -5; 1 |
|
|
|
|
|
|
- Вспомним ещё один вид логарифмических уравнений, которые решаются с помощью свойств логарифмов. Эти свойства вы видите на экране (слайд № 15), а так же они есть и у вас на столах (конспект). Воспользуемся этими свойствами и закрепим знания и умения решать логарифмические уравнения данного вида. Переходим к третьему уравнению и к доске пойдёт (Ф.И. обучающегося): log5х=3log54-log52 |
Обучающиеся смотрят экран.
2 обучающихся решают у доски с объяснением, пользуясь слайдом № 15; остальные записывают в тетради. log5х=3log54-log52 ОДЗ: х>0 log5х=log543-log52 log5х=log564-log52 |
|
Время |
Структурное построение урока |
Задачи |
МТО урока |
Межпредметные связи |
Деятельность |
|
|
Учителя |
Обучающихся |
|||||
|
|
|
|
|
|
И последнее уравнение пойдет решать… log3(2х+1)=log313 + 1
* Дополнительное задание log2х=2log23+log253
|
log5х=log564:2 log5х=log532 т.к. логарифмы равны, то будут равны и их подлогарифмические выражения: х=32 € ОДЗ Ответ: 32
log3(2х+1)=log313 + 1 ОДЗ: 2х+1>0 2х>-1 х>-1/2 log3(2х+1)=log313 + log33 log3(2х+1)=log313 ∙ 3 log3(2х+1)=log339 2х+1=39 2х=38 х=19 € ОДЗ Ответ: 19
log2х = 2log23 + log253 ОДЗ: х>0 log2х = log232 ∙ 53 log2х = log29 ∙ 53 х = 477 € ОДЗ Ответ: 477 |
|
10 мин. |
Закрепление (самостоятельная работа в виде теста с последующей взаимопроверкой) |
С помощью тес-тов проверить знания и умения учащихся по теме «Логариф-мические уравне-ния». Свойства логарифмов» |
Опорный конспект, тетрадь, канцелярские принадлежности, проектор, ПК, слайд. |
Информатика |
- У Вас перед глазами два варианта тестов (слайд № 16). Каждый решает свой вариант и в тетради напротив соответствующего задания выписываете букву с тем вариантом ответа, который Вы считаете верным. |
Обучающиеся слушают и смотрят на тест.
|
|
Время |
Структурное построение урока |
Задачи |
МТО урока |
Межпредметные связи |
Деятельность |
|
|
Учителя |
Обучающихся |
|||||
|
|
|
|
|
|
1 вариант. 1) Найдите число х: log4х=-3 а) 64 б) 1/64 в) -64 г) -1/64 2) Вычислите: log124+log1236 а) 4 б) 12 в) 6 г) 2 3) Найдите область определения функции у=log2(х-4) а) [4; +∞) б) (-∞; 4) в) (4; +∞) г) (-4; +∞;) 4) Решите уравнение: log7(х-1)=1 а) 8 б) 6 в) 7 г) -8 5) Решите уравнение: log3(5х-13)=log3(3х-7) а) -6 б) 10 в) 4 г) 3 6)* Решите уравнение: lg (2-х) = 2 lg 4 – lg 2
2 вариант. 1) Найдите число х: log7х=-2 а) 1/49 б) -49 в) 49 г) -1/49 2) Вычислите: lg13-lg130 а) 1 б) 10 в) -1 г) 2 3) Найдите область определения функции у=log2(х+4) а) [4; +∞) б) (-∞; 4) в) (4; +∞) г) (-4; +∞;) 4) Решите уравнение: log3(х-4)=1 а) 4 б) 7 в) 6 г) -8 |
Обучающиеся приступают к решению тестов. Ответы: 1 вариант. 1 – б 2 – г 3 – в 4 – а 5 – г 6)* lg (2-х) = 2 lg 4 – lg 2 ОДЗ: 2-х > 0 х < 2 2-х = 42 : 2 2-х = 16 : 2 2-х = 8 х = 2-8 х = - 6 € ОДЗ Ответ: - 6
2 вариант. 1 – а 2 – в 3 – г 4 – б 5 – г
|
|
Время |
Структурное построение урока |
Задачи |
МТО урока |
Межпредметные связи |
Деятельность |
|
|
Учителя |
Обучающихся |
|||||
|
|
|
|
|
|
5) Решите уравнение: log5(6х-17)=log5(2х-5) а) 5 б) 4 в) 8 г) 3 6)* Решите уравнение: lg (х+1) = 3 lg 2 + lg 4
По истечении 7-8 мин. преподаватель предлагает поменяться тетрадями с рядом сидящим и проверить полученные результаты по ответам, которые появляются на экране (слайд № 17). |
6)* lg (х+1) = 3 lg 2 + lg 4 ОДЗ: х+1 > 0 х > -1 х + 1 = 23 ∙ 4 х + 1 = 8 ∙ 4 х + 1 = 32 х = 31 € ОДЗ Ответ: 31
Обучающиеся проверяют результаты теста рядом сидящего с помощью слайда № 17 и выставляют ему предварительную оценку. |
|
3 мин. |
Подведение итогов |
С помощью дополнительных вопросов подвести итог урока. |
Опорный конспект преподавателя. |
|
Сегодня мы с вами на уроке закрепили решение лога-рифмических уравнений. 1. На чем основывается решение большинства из них?
2. Что называется логарифмом числа х по основанию а?
3. Что ещё необходимо знать для решения логарифми-ческих уравнений? Выставляются оценки за работу на уроке, подводятся итоги за работу по карточкам. |
Обучающиеся отвечают на вопросы.
1. Решение большинства из логарифмических уравнений основывается на определении логарифма. 2. Логарифмом числа х по основанию а называется показатель степени, в кото-рую нужно возвести число а, чтобы получить число х. 3. Свойства логарифмов.
Обучающиеся слушают. |
|
Время |
Структурное построение урока |
Задачи |
МТО урока |
Межпредметные связи |
Деятельность |
|
|
Учителя |
Обучающихся |
|||||
|
1 мин. |
Домашнее задание |
Развивать мышление. |
Тетради, канцелярские принадлежности |
|
Задание на дом: придумать и решить два уравнения таких, чтобы 1-ое решалось по определению логарифма, а 2-ое с использованием свойств логарифма. Урок окончен. Спасибо за внимание (слайд 18) |
Обучающиеся записывают домашнее задание. |
|
1 мин. |
Рефлексия |
|
|
|
|
|
Тема урока: «Повторение решения логарифмических уравнений»
Цели урока: 1) Обобщить и закрепить понятия: логарифмической функции и
логарифма числа.
2) Повторить основные свойства логарифма.
3) Закрепить умения применять эти понятия при решении уравнений.
Оснащение урока: ПК, проектор, экран, доска, мел; программное обеспечение: электронный учебник «Математика, часть I», опорные конспекты, карточки для самостоятельного решения, презентация.
Межпредметные связи: Информатика: - Создание презентации;
- Применение электронного учебника
«Математика, часть I».
Литература: - Развитие грамотной речи.
Ход урока.
|
Преподаватель |
Учащиеся |
||||||
|
1. Организационный момент – 2 мин. |
|||||||
|
1. Приветствие учащихся. 2. Объявление темы урока, основных целей и хода урока ( слайды 1, 2). |
1. Сидят на своих местах. 2. Записывают тему урока: «Повторение решений логарифмических уравнений» |
||||||
|
2. Устная работа + Повторение и обобщение знаний по теме: «Логарифмическая функция и её свойства» и «Решение показательных уравнений» - 8 мин. |
|||||||
|
Приглашает 1 учащегося к доске и просит выполнить задание по карточке на повторение по теме «Логарифмическая функция и её свойства» с последующим объяснением: Карточка: 1) какая функция называется логарифмической; 2) построить график функции у=log2х и перечислить её свойства.
2 учащихся решают задания на местах по карточкам на повторение и закрепление по темам «Область определения», «Решение показательных уравнений» Карточка 1: 1) Найдите область определения функции у=log5(2х-1);
2) Решите уравнение: 4х+1+4х=320
Карточка 2: 1) Найдите область определения функции у=√2х-16
|
Ответы учащегося: 1) 2х-1>0 х>1/2 2х>1 Ответ: (1/2;+∞)
2) 4х+1+4х = 320 4х ∙5 = 320 4х = 43 4х ∙4+4х = 320 4х = 320:5 х = 3 4х(4+1) = 320 4х = 64 Ответ: 3 Ответы учащегося: 1) 2х-16 ≥ 0 2х ≥ 16 2х ≥ 24 Т.к. в показательной функции у=2х основание больше 1, то функция возрастает. Имеем: х ≥ 4 Ответ: [4;+∞)
|
||||||
|
Преподаватель |
Учащиеся |
||||||
|
2) Решите уравнение:
Остальные решают устно: 1 Рассуждалки: 1. а) Это такая штука, в которой что-то не знаешь, а потом вдруг узнаешь, если захочешь это сделать – и сделаешь (слайд 3). б) Иногда задачи решаются только с его помощью. в) Не знаю, есть ли у него листья и стебли, но корни у него есть. Может 1, а может больше. И только у некоторых нет и корней. г) Во 2-м классе они – простые, в 7-м – линейные, в 8-м – квадратные, а в 11-м – логарифмические.
б) Кто-то их любит, а кто-то нет, потому что на них надо много думать головой, писать, решить, отвечать. в) На нем говорят, что неправильно решил задачу или примеры.
г) А может времени не хватило, ведь он всего 45 мин.
2. Ребусы: (слайды № 1, 2)
* 3. Загадалки: 1) Французский математик, известна его теорема про корни квадратного уравнения 2) Кто из великих русских писателей занимался составлением арифметических задач?
_ Теперь проверим, как у нас с заданием справилась Гульназ у доски. Слушаем тебя. Карточка: 1) какая функция называется логарифмической;
2) построить график функции у=log2х и перечислить её свойства.
* Дополнительный вопрос: Когда логарифмическая функция убывает? |
2) 32х+3 = (243)-1 2х = - 8 32х+3 = (35)-1 х = - 4 Ответ: - 4
Ответы учащихся:
1. Уравнения.
2. Урок математики
Ответы учащихся: 1) Геометрия 2) Уравнение 3) Показатель 4) Диагональ
Ответы учащихся: 1) Виет
2) Толстой
1. Определение: Функцию, заданную формулой у=logах, называют логарифмической функцией с основанием а. 2. Свойства: 4) Д(у) = (0; +∞) 5) Е(у) = R 6) Логарифмическая функция на все области определения возрастает (при а>1). * Убывает, когда основание больше 0, но меньше 1. |
||||||
|
Преподаватель |
Учащиеся |
||||||
|
3. Повторение решений логарифмических уравнений – 15 мин. |
|||||||
|
- Мы переходим к нашей теме: «Повторение решения логарифмических уравнений». Чтобы напомнить вам как решаются логарифмические уравнения, попрошу посмотреть на экран.
- Как уже было сказано, такие уравнения решаются по определению логарифма. Итак, на экране мы видим определение логарифма. Кто нам его прочитает? (слайд № 13)
- Рассмотрим пример решения логарифмического уравнения (слайд № 14) и решим устно следующие уравнения.
- Сейчас мы переходим к закреплению знаний и умений по данной теме. Первый пример из конспекта решу я, чтобы еще раз напомнить алгоритм решения логарифмических уравнений по определению.
- Теперь я предлагаю вам решить второе уравнение и приглашаю к доске (Ф.И. обучающегося) log4(5х+8) = 3
- Решим ещё одно уравнение по определению. К доске, пожалуйста (Ф.И. обучающегося). log2(х2+4х-3) = 1
- Вспомним ещё один вид логарифмических уравнений, которые решаются с помощью свойств логарифмов. Эти свойства вы видите на экране (слайд № 15), а так же на своих столах (конспект). |
Учащиеся слушают объяснения с экрана.
Один из учеников зачитывает определение логарифма: Определение: Логарифмом положительного числа х по основанию а (а>0, а=1) называется показатель степени, в которую нужно возвести число а, чтобы получить число х.
(слайд № 14)
Решают уравнение совместно с преподавателем.
1 учащийся решает у доски с объяснением, остальные записывают в тетради.
log4(5х+8) = 3 ОДЗ: 5х+8>0 По опред-ю логарифма 5х>-8 5х+8 = 43 х>-8:5 5х+8 = 64 х>-1,6 5х = 64-8 5х = 56 х = 56:5 х = 11,2 € ОДЗ Ответ: 11,2
log2(х2+4х-3)=1 ОДЗ: х2+4х-3>0 По опред-ю логарифма х2+4х-3=2 х2+4х-5=0 по теореме Виета: х1+х2 = - 4 х1 = - 5 х1∙х2 = - 5 х2 = 1 Проверка: х1 = - 5 € ОДЗ log2((-5)2+4∙(-5)-3) = = log2(25-20-3) = log22 = 2 х2 = 1 € ОДЗ log2(12+4∙1-3)=log2(1+4-3) = = log22 = 2 Ответ: -5; 1
Учащиеся слушают объяснения с экрана.
|
||||||
|
Преподаватель |
Учащиеся |
||||||
|
Воспользуемся этими свойствами, прослушанным материалом и закрепим наши знания и умения решать логарифмические уравнения данного вида. Итак, к доске пойдёт (Ф.И. обучающегося) log5х = 3log54 - log52
- Те, кто решает вперёд и успеет выполнить ещё и дополнительное задание, поднимете руку, я проверю и поставлю оценку в журнал.
- И последнее уравнение пойдет решать (Ф.И. обучающегося). log3(2х+1) = log313 + 1
* Дополнительное задание log2х = 2log23 + log253
|
1 учащийся решает у доски с объяснением, пользуясь слайдом № 5; остальные записывают в тетрадях. log5х = 3log54 - log52 ОДЗ: х>0 log5х = log543 - log52 log5х = log564 - log52 log5х = log564:2 log5х = log532 т.к. логарифмы равны, то будут равны и их подлогарифмические выражения: х = 32 € ОДЗ Ответ: 32
log3(2х+1) = log313 + 1 ОДЗ: 2х+1>0 log3(2х+1) = log313 + log33 2х>-1 log3(2х+1) = log313 ∙ 3 х>-1/2 log3(2х+1) = log339 2х+1 = 39 2х = 38 х=19 € ОДЗ Ответ: 19
log2х = 2log23 + log253 ОДЗ: х>0 log2х = log232 ∙ 53 log2х = log29 ∙ 53 х = 477 € ОДЗ Ответ: 477 |
||||||
|
4. Закрепление (тест с последующей взаимопроверкой) – 10 мин. |
|||||||
|
- У Вас перед глазами два варианта тестов. Каждый решает свой вариант в тетради и напротив соответствующего задания выписывает букву с вариантом ответа, который Вы считаете верным. Дополнительное 6-е задание для тех, кто быстро выполнит первые 5-ть и у кого останется время. В 6-м задании показать само решении, и оно будет оцениваться отдельно. 1 вариант. 1) Найдите число х: log4х = -3 а) 64 б) 1/64 в) -64 г) -1/64 2) Вычислите: log124 + log1236 а) 4 б) 12 в) 6 г) 2 3) Найдите область определения функции у = log2(х-4) а) [4; +∞) б) (-∞; 4) в) (4; +∞) г) (-4; +∞) 4) Решите уравнение: log7(х-1) = 1 а) 8 б) 6 в) 7 г) -8 5) Решите уравнение: log3(5х-13) = log3(3х-7) а) -6 б) 10 в) 4 г) 3 6)* Решите уравнение: lg (2-х) = 2 lg 4 – lg 2 |
Учащиеся решают тест в тетрадях.
Ответы: 1 вариант. 1 – б 2 – г 3 – в 4 – а 5 – г 6)* lg (2-х) = 2 lg 4 – lg 2 ОДЗ: 2-х > 0 2-х = 42 : 2 х < 2 2-х = 16 : 2 2-х = 8 х = 2-8 х = - 6 € ОДЗ Ответ: - 6 |
||||||
|
Преподаватель |
Учащиеся |
||||||
|
2 вариант. 1) Найдите число х: log7х = -2 а) 1/49 б) -49 в) 49 г) -1/49 2) Вычислите: lg13 - lg130 а) 1 б) 10 в) -1 г) 2 3) Найдите область определения функции у = log2(х+4) а) [4; +∞) б) (-∞; 4) в) (4; +∞) г) (-4; +∞) 4) Решите уравнение: log3(х-4) = 1 а) 4 б) 7 в) 6 г) -8 5) Решите уравнение: log5(6х-17) = log5(2х-5) а) 5 б) 4 в) 8 г) 3 6)* Решите уравнение: lg (х+1) = 3 lg 2 + lg 4
- Время истекло (7 мин.). Я предлагаю вам поменяться тетрадями с рядом сидящим и проверить результаты по ответам, которые Вы видите на экране и оценить работу по следующим критериям (слайд № 7).
|
2 вариант. 1 – а 2 – в 3 – г 4 – б 5 – г
6)* lg (х+1) = 3 lg 2 + lg 4 ОДЗ: х+1 > 0 х > -1 х + 1 = 23 ∙ 4 х + 1 = 8 ∙ 4 х + 1 = 32 х = 31 € ОДЗ Ответ: 31
Учащиеся проверяют результаты теста рядом сидящего с помощью слайда № 7 и выставляют ему предварительную оценку.
|
||||||
|
5. Подведение итогов – 4 мин. |
|||||||
|
- Сегодня мы с вами на уроке закрепили решение логарифмических уравнений. 1. На чем основывается решение большинства из них?
2. Что называется логарифмом числа х по основанию а?
3. Что ещё необходимо знать для решения логарифмических уравнений?
Оценки за работу выставляются по ходу урока, а за карточки после подведения итогов. |
Учащиеся отвечают на вопросы.
1. Решение большинства из логарифмических уравнений основывается на определении логарифма. 2. Логарифмом числа х по основанию а называется показатель степени, в которую нужно возвести число а, чтобы получить число х. 3. Свойства логарифмов
Учащиеся слушают. |
||||||
|
6. Домашнее задание – 1 мин. |
|||||||
|
Задание на дом: Придумать и решить два уравнения таких, чтобы 1-ое решалось по определению логарифма, а 2-ое с использованием свойств логарифма.
|
Учащиеся записывают домашнее задание. |
||||||
ХОД УРОКА
1. Организационный момент.
2. Устная работа, работа с карточками.
3. Повторение решений логарифмических уравнений.
4. Закрепление (тест с элементом взаимопроверки).
5. Подведение итогов.
ОПОРНЫЙ КОНСПЕКТ
1. Определение логарифма числа: ![]()
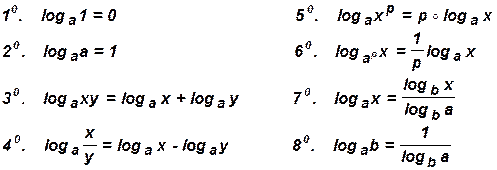 |
2. Свойства логарифмов:
1. Повторение.
Решите уравнения: 1. log4(5х+8)=3 3. log5х=3log54-log52
2. log2(х2+4х-3)=1 4. log3(2х+1)=log313 + 1
*5. log2х=2log23+log253
4. Закрепление (тест с элементом взаимопроверки).
ТЕСТ
|
I вариант 1) Найдите число х: log4х = -3 а) 64 б) 1/64 в) -64 г) -1/64 2) Вычислите: log124+log1236 а) 4 б) 12 в) 6 г) 2 3) Найдите область определения функции у = log2(х-4) а) [4; +∞) б) (-∞; 4) в) (4; +∞) г) (-4; +∞) 4) Решите уравнение: log7(х-1) = 1 а) 8 б) 6 в) 7 г) -8 5) Решите уравнение: log3(5х-13) = log3(3х-7) а) -6 б) 10 в) 4 г) 3 6)* Решите уравнение: lg (2-х) = 2 lg 4 – lg 2 |
|
II вариант 1) Найдите число х: log7х = -2 а) 1/49 б) -49 в) 49 г) -1/49 2) Вычислите: lg13-lg130 а) 1 б) 10 в) -1 г) 2 3) Найдите область определения функции у = log2(х+4) а) [4; +∞) б) (-∞; 4) в) (4; +∞) г) (-4; +∞) 4) Решите уравнение: log3(х-4) = 1 а) 4 б) 7 в) 6 г) -8 5) Решите уравнение: log5(6х-17) = log5(2х-5) а) 5 б) 4 в) 8 г) 3 6)* Решите уравнение: lg (х+1) = 3 lg 2 + lg 4 |
Приложение
Карточка (у доски):
1) Какая функция называется логарифмической;
2) Построить график функции у = log2х и перечислить её свойства.
Дополнительный вопрос:
При каком условии логарифмическая функция убывает?
Карточка 1:
1) Найдите область определения функции у = log5(2х-1);
2) Решите уравнение: 4х+1+4х=320
Карточка 2:
1) Найдите область определения функции у=√2х-16
2) Решите уравнение:
![]()
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.