Тема : Площадь трапеции

Дидактическая цель урока: создать условия для осознания новой учебной информации средствами технологии проблемного обучения.

Цели урока:

 

·         образовательные: формировать навык выведения формулы для вычисления площади трапеции, закрепить навыки решения задач по выведенной формуле;

·         развивающие: развитие воображения, сравнения, обобщения;

·         воспитательные: формирование коммуникативных умений.

 

Тип урока: урок первичного предъявления новых знаний
Целевое назначение: первичное усвоение новых предметных и метапредметных знаний.

 

Результативность обучения: воспроизведение своими словами правил, понятий, алгоритмов, выполнение действий по образцу.

Формы организации учебной деятельности: индивидуальная, фронтальная, работа в группах.

Методы обучения: репродуктивный, частично-поисковый.

 

Ход урока

1. Организационный момент.

Учитель: Здравствуйте ребята!  Сегодня урок у нас необычный, к нам пришли гости. Надеюсь на вашу поддержку и нашу общую плодотворную работу.

 

2. Постановка цели и задач урока. Мотивация учебной деятельности учащихся

 

Я хочу, чтобы девизом нашего урока стали слова одного вьетнамского мудреца. «Дойти можно лишь тогда, когда идешь. Узнать можно лишь тогда, когда учишься».

Сегодня каждый из вас на уроке может сделать маленькое открытие. Для этого от вас требуется внимание, активность и желание работать. 

Мы с вами вспомним  все, что изучили о площадях. И постараемся сделать открытие новой формулы.

3. Актуализация знаний.

1.   Каким символом обозначается площадь?  (Нарисуйте в воздухе)

2.   Какие единицы измерения площадей вы знаете? (1мм², 1см², 1дм², 1м², 1км²; 1 а, 1 га – в сельском хозяйстве

3.   Если многоугольник составлен из нескольких многоугольников, то как найти площадь этого многоугольника?

4.     Площади каких геометрических фигур мы умеем находить? Как? (площадь квадрата, прямоугольника, треугольника, параллелограмма)

5.       Где применяется на практике знание формул площадей? (В строительстве, в сельском хозяйстве.)

 

 

 

1)  Ответьте на вопросы - Сума углов треугольника? 180 - Сумма углов выпуклого четырехугольника? 360 - Свойства равнобедренного треугольника? В равнобедренном треугольнике углы при основании равны Биссектриса, проведенная к основанию, является медианой и высотой 2) Соотнесите четырехугольник и формулу его периметра Р = a+b+c+d Р = (a+b) *2   Р= 4*а P = a+b+c Р = (a+b) *2   2) Соотнесите четырехугольник и формулу его площади S = S =   S = S = b*h S = a*b

 

 

 

1) Тест по проверке теоретического материала.

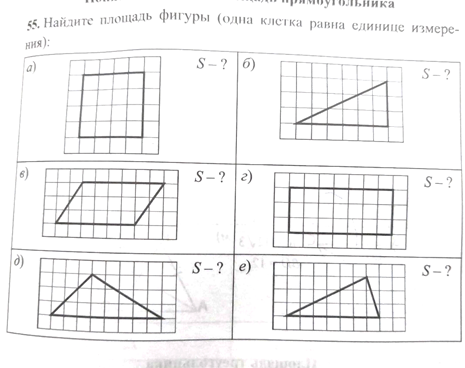
1.   Выберите верные утверждения:

а) площадь прямоугольника равна произведению двух его сторон; б) площадь квадрата равна квадрату его стороны;

в) площадь прямоугольника равна удвоенному произведению двух его соседних сторон.

2.   Закончите фразу: площадь треугольника равна половине произведения…

а) его сторон;

б) его стороны и высоты, проведенной к этой стороне;

 в) его диагоналей.

3.   По формуле S= a∙h_а можно вычислить площадь:

а) параллелограмма;

  б) треугольника;

в) прямоугольника.

 

4.   Выберите верное утверждение. Площадь прямоугольного треугольника равна:

а) половине произведения его стороны на какую-либо высоту;

 б) половине произведения его катетов;

в) произведению его стороны на проведенную к ней высоту.

–       А теперь поменяйтесь тетрадями с соседом и выполните проверку. За каждое правильно выполненное задание 1 балл.

Ответы: 1) б; 2) б; 3) а; 4)б;

 

III.                 Целеполагание и определение путей достижения цели

– Ребята, послушайте высказывания, и выясните о какой фигуре пойдет речь на уроке. Свой ответ обоснуйте.

–   Фигура представляет собой выпуклый многоугольник.

–   Сумма её внутренних углов 360 градусов.

–   А сумма внутренних углов, прилежащих к одной стороне 180 градусов.

–   Данная фигура хорошо разбивается на параллелограмм и треугольник.

– Что это за фигура?

– Правильно, это трапеция! Итак, сегодня мы поговорим о трапеции.

–   И сегодня вы выведем формулу нахождения площади трапеции?

IV.   Изучение нового материала.

Тема сегодняшнего урока: “Площадь трапеции”.

–   цель нашего урока: найти удобный способ вычисления площади трапеции.

–   Поисками этого способа мы сейчас и займёмся.

–   Сначала вспомним определение трапеции. (Трапеция – это четырёхугольник, у которого две стороны параллельны, а две другие – нет.)

–   Как называются стороны трапеции? (Основания и боковые.)

 

–   Трапе́ция (от др.-греч. τραπέζιον — «столик» от τράπεζα — «стол»)

 

 

–   Сегодня мы будем искать более удобный, более точный способ нахождения  площади трапеции. У каждого из вас на столе лежат модели трапеции. Вы можете разбить её на такие фигуры, площади которых мы умеем находить. Разбивать с помощью карандаша и линейки. Используя свойства площадей, найдите площадь трапеции.

 

–   Итак, работаем в парах! (Учащиеся работают: разбивают трапецию на части, выполняют необходимые измерения и вычисляют площади получившихся  фигур.)

–   Подведём итоги: назовите ваши результаты: S_тр= …

–   Как вы находили S_тр?

 

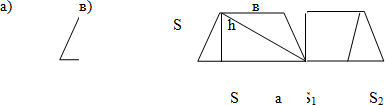–   Какой способ лучше? (Последний.) S = S₁ + S₂= ½ à·h + _.½ â·h= ½ (à + в)·h

Итак, S_тр= ½ (à + в)·h, где а и в – основания, h – высота.

Это и есть формула для вычисления площади трапеции. Записываем в тетрадь.

Мы с вами сделали открытие!

«5 минут ОГЭ»

   

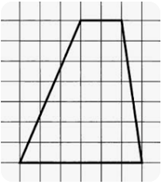
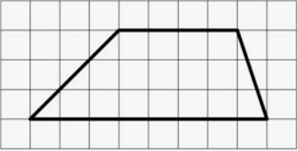
–   Сравнить полученную формулу и формулировку с предложенными в учебнике. Каждый ученик записывает в тетрадь формулу площади трапеции и формулировку, выбранную им.

V.   Первичное закрепление.

Решение задач по готовым чертежам

 

.

VI.   Информация о домашнем задании, инструктаж по его выполнению

VII.       Итог урока. Рефлексия

Выставление оценок и их комментирование.

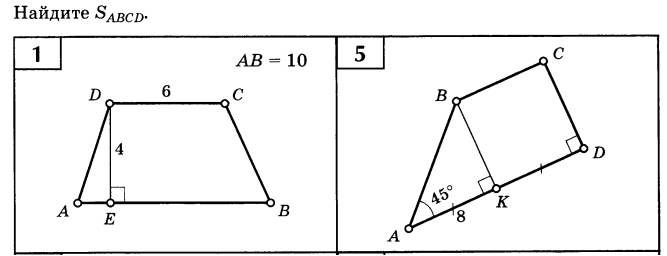
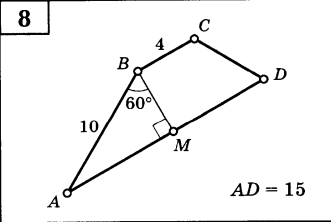
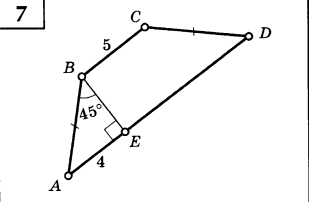
Дается оценка работы класса, отдельных учащихся

Урок сегодня завершен, П. 53 № 480

 

Лист заданий

1 Соотнесите четырехугольник и формулу его периметра

1		А	Р = a+b+c+d	1 –   2 –   3 –   4 –   5 -
2		Б	Р = (a+b) *2
3		В	Р= 4*а
4		Г	P = a+b+c
5		Д	Р = (a+b) *2

         

2 Соотнесите четырехугольник и формулу его площади

1		А	S = a*b	1 –   2 –   3 –   4 –
2		Б	S =
3		В	S =
4		Г	S = b*h

 

 

3. Тест по проверке теоретического материала

1.   Выберите верные утверждения:

а) площадь прямоугольника равна произведению двух его сторон;

б) площадь квадрата равна квадрату его стороны;

в) площадь прямоугольника равна удвоенному произведению двух его соседних сторон.

2. Закончите фразу: площадь треугольника равна половине произведения…

а) его сторон;

б) его стороны и высоты, проведенной к этой стороне;

в) его диагоналей.

3. По формуле S= a∙h_а можно вычислить площадь:

а) параллелограмма;

б) треугольника;

в) прямоугольника.

4. Выберите верное утверждение. Площадь прямоугольного треугольника равна:

а) половине произведения его стороны на какую-либо высоту;

 б) половине произведения его катетов;

в) произведению его стороны на проведенную к ней высоту.    

 

                               

 

 

 

 

Скачано с www.znanio.ru