Подобие треугольников

1.   Какие треугольники называются подобными?

2.   Сформулируйте признаки подобия треугольников.

3.   Чему равно отношение периметров подобных треугольников?

4.   Чему равно отношение площадей подобных треугольников?

5.   Сформулируйте свойство биссектрисы угла.

6.   Найти 𝑥: 

      a.                                                          e.

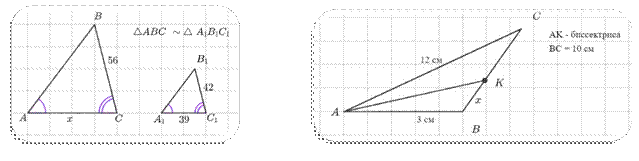1

 b. 

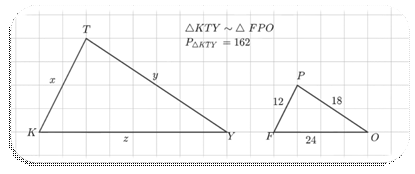 c.  

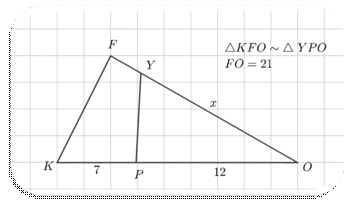
        7.                                                                   f. 

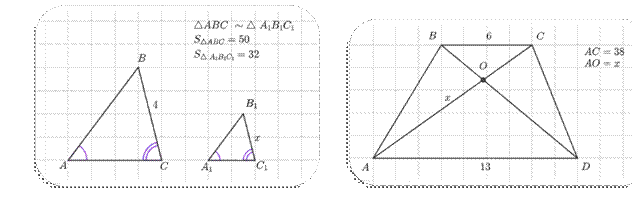
См/р

1.   Выберите верные утверждения:

a.   Биссектриса треугольника делит пополам сторону, к которой проведена.

b.   Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны.

c.   Если две стороны и угол одного треугольника равны соответственно двум сторонам и углу другого треугольника, то такие треугольники равны.

d.   Если две стороны одного треугольника соответственно равны двум ₂ сторонам другого треугольника, то такие треугольники равны.

e.   Если три угла одного треугольника равны соответственно трём углам другого треугольника, то такие треугольники равны.

f.     Все равнобедренные треугольники подобны.

2.   Чему равно отношение периметров подобных треугольников? Ответ: _________

3.   Чему равно отношение площадей подобных треугольников? Ответ: _________

4.   Сформулируйте свойство биссектрисы угла. (Можно при помощи чертежа.)

5.   Найти 𝑥: 

a.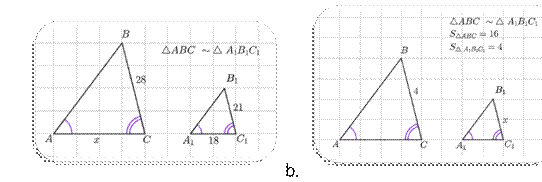

Домашнее задание: 

1.   Найти 𝑥:

a. 

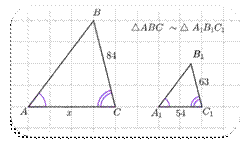
    3 b. 

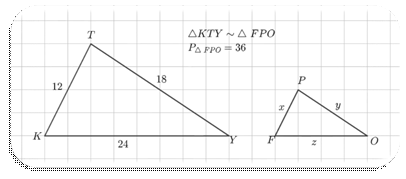 c. 

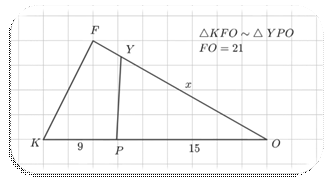
d. 

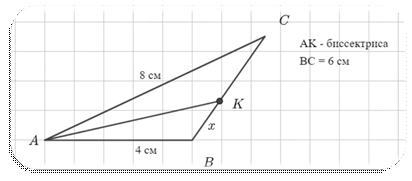
2.   Диагонали АС и BD трапеции ABCD с основаниями ВС и AD пересекаются в точке О, ВС = 2, AD = 8, АС = 40 . Найдите АО.

3.   Выполнить работу над ошибками по см/р