Добавить материал

и получить 10 документов
и свидетельство автора

Семенова Альбина Михайловна

«Показательная функция, свойства и график»

Разработки уроков
docx
15.05.2023

Публикация педагогических разработок

Бесплатное участие. Свидетельство автора сразу.
Мгновенные 10 документов в портфолио.

Добавить материал

Данная методическая разработка по теме «Показательная функция, свойства и график» яв-ляется уроком изучения нового материала. Урок построен так, чтобы обучающиеся, опираясь на ранее полученные знания, могли вывести формулы сами. Материал урока направлен на изучение показательной функции, свойства и график.

показательная функция,свойства и график.docx

Филиал бюджетного профессионального образовательного учреждения Чувашской Республики

«Чебоксарский медицинский колледж»

Министерства здравоохранения Чувашской Республики в городе Канаш

РАССМОТРЕНО и ОДОБРЕНО

на заседании

ЦМК ОГСЭ

Протокол № ____

«____» _______________ 20 ___ г.

Председатель ЦМК

____________Л.М Иванова

утверждено

Зав. филиалом БПОУ «ЧМК»

МЗ Чувашии в г. Канаш

____________ Т.Э Фадеева

Методическая разработка теоретического занятия

Показательная функция,

свойства и график.

учебная дисциплина БД. 04 Математика

специальность 34.02.01Сестринское дело

(базовая подготовка)

Канаш, 2021

Составитель: Семенова А.М., преподаватель высшей квалификационной категории филиала БПОУ ЧР «Чебоксарский медицинский колледж» Министерства здравоохранения Чувашии в г. Канаш

Рецензент: Иванова Л.М., преподаватель, высшей квалификационной категории филиала БПОУ ЧР «Чебоксарский медицинский колледж» Министерства здравоохранения Чувашии в г. Канаш

Аннотация

Данная методическая разработка по теме «Показательная функция, свойства и график» является уроком изучения нового материала. Урок построен так, чтобы обучающиеся, опираясь на ранее полученные знания, могли вывести формулы сами. Материал урока направлен на изучение показательной функции, свойства и график.

СОДЕРЖАНИЕ

ВВЕДЕНИЕ. 3

1. методический блок. 4

1.1. Учебно-методическая карта. 4

Формы деятельности. 4

1.2. Технологическая карта. 8

2. Информационный блок. 10

2.1. План лекции. 10

2.2 Текст лекции. 11

2.3. Глоссарий. 18

3. Контролирующий блок

ВВЕДЕНИЕ

Данная методическая разработка по теме «Показательная функция, свойства и график» является уроком изучения нового материала. Материал урока направлен на развитие логического мышления, алгоритмической культуры, интуиции, навыков исследовательской деятельности, творческих способностей обучающихся. Структура урока: постановка цели и задач урока; повторение умений и навыков, являющихся опорой для восприятия новой темы; проведение проверочных упражнений (устная работа); изучение показательной функции, свойства и график. Упражнения на закрепление данного алгоритма; тренировочные упражнения по образу и подобию в виде самостоятельной работы; самоконтроль обучающихся.
Создание проблемных ситуаций на уроках математики повышает интерес к предмету, вносит разнообразие и эмоциональную окраску в учебную работу, снимает утомление, развивает внимание, сообразительность.

1. МЕТОДИЧЕСКИЙ БЛОК

1.1. Учебно-методическая карта

Тема занятия	Показательная функция, свойства и график.
Учебная дисциплина	БД.04 Математика
Специальность	34.02.01 Сестринское дело (базовая подготовка)
Курс	I
Группа	9М-11-20, 9М-12-20, 9М-13-20,9М-14-20, 9М-15-20.
Место проведения	Кабинет № 5
Продолжительность занятия	90 мин.
Характеристика занятия	Вид	Вид занятия Лекция текущая, обзорная.
	Тип	Типы учебных занятий урок изучения нового материала; комбинированный урок
	Форма	Изложение, рассказ, объяснение с демонстрацией наглядных пособий. Формы деятельности Фронтальная.
Технологии обучения	Традиционная технология обучения Технология развивающего обучения
Методы обучения	Метод Репродуктивный: упражнения, действия по алгоритму. Интерактивные методы – практическая отработка осваиваемых знаний, умений, навыков на уровне компетенций
Средства обучения	1.По характеру воздействия на обучаемых: ИКТ - презентации; 2.По степени сложности: простые: учебники, печатные пособия.
Методическая цель	Методическая цель - отрабатывать методику контроля результатов выполнения письменных упражнений. - реализовывать индивидуальный дифференцированный подход в процессе выполнения обучающимися заданий для самостоятельной работы;
Цели и задачи занятия	Воспитательная			Формулировать интеллектуальных, нравственных, эмоционально-волевых качеств у обучающихся.		Воспитывать положительное отношение к приобретению новых знаний; Воспитывать ответственность за свои действия и поступки; Вызвать заинтересованность новым для студентов подходом изучения математики. Воспитывать интерес к математике путём введения разных видов закрепления материала: устной работой, работой с учебником, работой у доски, ответами на вопросы и умением делать самоанализ, самостоятельной работой; стимулированием и поощрением деятельности учащихся.
	Образовательная			Рассмотреть свойства показательной функции и ее график Выяснить значение показательной функции Применять полученные знания в простейших ситуациях. Систематизировать знания о показательной функции.		Учиться отличать показательную функцию от других функций, в частности от степенной функции. Учиться строить график показательной функции Знать свойства показательной функции Выяснить значение показательной функции в природе и технике
	Развивающая			Развитие речи, мышления, сенсорной восприятие внешнего мира через органы чувств сферы;		Формировать навыки познавательного мышления. Продолжить развитие умения выделять главное. Продолжить развитие умения устанавливать причинно-следственные связи. Развивать навыки и умения, в выполнении заданий по теме, умение работать в группе и самостоятельно. Развивать логическое мышление, правильную и грамотную математическую речь, развитие самостоятельности и уверенности в своих знаниях и умениях при выполнении разных видов работ. развивать познавательный интерес.
Планируемый результат	Уметь	Отличать показательную функцию от других функций, в частности от степенной функции. Строить график показательной функции Знать свойства показательной функции
	Знать	Определение показательной функции, свойства и график.. Значение показательной функции в природе и технике.
Формирование компетенций у обучающихся	Общие (ОК)				Л1. Сформированность представлений о математике как универсальном языке науки, средстве моделирования явлений и процессов, идеях и методах математики; Л5. Готовность и способность к образованию, в том числе самообразованию, на протяжении всей жизни; сознательное отношение к непрерывному образованию как условию успешной профессиональной и общественной деятельности; Л8. Отношение к профессиональной деятельности как возможности участия в решении личных, общественных, государственных, общенациональных проблем; М2. Умение продуктивно общаться и взаимодействовать в процессе совместной деятельности, учитывать позиции других участников деятельности, эффективно разрешать конфликты; М5. Владение языковыми средствами: умение ясно, логично и точно излагать свою точку зрения, использовать адекватные языковые средства;
	Профессиональные (ПК)				П1. Сформированность представлений о математике как части мировой культуры и месте математики в современной цивилизации, способах описания явлений реального мира на математическом языке; П3. Владение методами доказательств и алгоритмов решения, умение их применять, проводить доказательные рассуждения в ходе решения задач; П4. Владение стандартными приемами решения рациональных и иррациональных, показательных, степенных, тригонометрических уравнений и неравенств, их систем; использование готовых компьютерных программ, в том числе для поиска пути решения и иллюстрации решения уравнений и неравенств;
Межпредметные связи	Входящие		История				Показательная функция.
	Выходящие		Геометрия


Внутрипредметные	Алгебра, геометрия
	Действительные числа
Оснащение занятия	Методическое			Методическая разработка занятия.
	Материально-техническое			Ручка, карандаш, тетрадь, линейка.
	Информационное			Компьютер, интерактивная доска.
Список литературы	Основная			1.Алимов, Ш. А. Алгебра и начала математического анализа (базовый и углубленный уровни)10—11 классы / Ш.А. Алимов — М., 2018. – с.455. 2.Колягин, Ю.М. Математика: алгебра и начала математического анализа. Алгебра и начала математического анализа (базовый и углубленный уровни). 11 класс / М. В Ткачева., Н. Е Федерова. — М., 2018. - 384 с.
	Дополнительная			1 Александров А.Д., Геометрия / А.Л.Вернер, В.И. Рыжик (базовый и профильный уровни). 10—11 кл. – 2017. – 344 с. 2. Богомолов, И.Д. Математика: учебник / И.Д. Богомолов. – М., 2018. - 384 с.
	Интернет-ресурсы			1. Калашникова В.А. Методическое пособие: «Конспекты лекций по математике» [Электронный ресурс] /В.А. Калашникова. 2. Яковлев Г.Н. Алгебра и начала анализа (Математика для техникумов) [Электронный учебник] /Г.Н Яковлев. - Режим доступа: http://lib.mexmat.ru/books/78472. 3.http://fcior.edu.ru/ - Федеральный центр информационно-образовательных ресурсов 4.http://school-collection.edu.ru/ - Единая коллекция цифровых образовательных ресурсов

1.2. Технологическая карта

Деятельность преподавателя	Деятельность обучающихся	Методическое обоснование		Формируемые ОК и ПК
1. Организационный этап -5 мин.
Проверяет готовность обучающихся к занятию. дает положительный эмоциональный настрой, организует, проверяет готовность уч-ся к уроку	Готовятся к началу занятия.	Включение обучающихся в деятельность на личностно значимом уровне.		ОК 1, ОК 4. П1.
2. Этап всесторонней проверки домашнего задания - 10мин.
Выявляет правильность и осознанность выполнения всеми обучающимися домашнего задания; устранить в ходе проверки обнаруженные пробелы в знаниях.	По очереди комментируют свои решения. Приводят примеры. Пишут под диктовку.	Повторение изученного материала, необходимого для открытия нового знания, и выявление затруднений в индивидуальной деятельности каждого обучающегося.		ОК1, ПК 1, ПК4
3. Постановка цели и задач занятия. Мотивация учебной деятельности обучающихся - 5 мин.
Озвучивает тему урока и цель, уточняет понимание обучающегося поставленных целей урока. Эмоциональный настрой и готовность преподавателя на урок.	Эмоционально настраиваются и готовятся обучающихся на урок. Ставят цели, формулируют тему урока.	Обсуждение затруднений; проговаривание цели урока в виде вопроса, на который предстоит ответить. Методы, приемы, средства обучения: побуждающий от проблемы диалог, подводящий к теме диалог.		ОК 1, ОК 4. П1.
4. Актуализация знаний - 30 мин.
Уточняет понимание обучающимися поставленных целей занятия. Выдвигает проблему. Создает условия, чтобы обучающийся смогли систематизировать знания о множестве действительных чисел, имели представление о пределе числовой последовательности	Под диктовку, все выполняют задание, а один проговаривает вслух.		Создание проблемной ситуации. Уч-ся- фиксируют индивидуальные затруднения . Создание условия, чтобы обучающийся смогли систематизировать знания о множестве действительных чисел.	ОК 1, ОК 4. П1.
5. Первичное усвоение новых знаний - 10 мин.
Создаёт эмоциональный настрой на усвоение новых знаний.	Внимательно слушают, записывают под диктовку в тетрадь.	Создание условий, чтобы обучающийся смогли систематизировать знания о множестве действительных чисел.		ОК1, ПК 1, ПК4
6. Первичная проверка понимания - 10 мин.
Проводит параллель с ранее изученным материалом. Проводит беседу по уточнению и конкретизации первичных знаний;	Отвечают на заданные вопросы преподавателем.	Осознание степени овладения полученными знаниями - каждый для себя должен сделать вывод о том, что он уже умеет.		ОК1, ПК 1, ПК4
7. Первичное закрепление - 5 мин.
Контролирует выполнение работы. Осуществляет: индивидуальный контроль; выборочный контроль. Побуждает к высказыванию своего мнения. Показывает на доске решение, опираясь на алгоритм.	записывают решение, остальные решают на местах, потом проверяют друг друга;	Тренировка и активизация употребления новых знаний, включение нового в систему Режим работы: устная, письменная, фронтальная, индивидуальная.		ОК1, ПК 1, ПК4
8. Контроль усвоения, обсуждение допущенных ошибок и их коррекция (подведение итогов занятия 5 мин
Отмечает степень вовлеченности обучающихся в работу на занятии. Задает вопросы по обобщению материала.	Под диктовку, все выполняют задание, а один проговаривает вслух;	Оценивание работу обучающихся, делая акцент на тех, кто умело взаимодействовал при выполнении заданий		ОК 1, ОК 4. П1.
9. Информация о домашнем задании, инструктаж по его выполнению 5 мин
Обсуждение способов решения домашнего задания. Записывает номера заданий на доске.	Обобщают полученные знания, делают вывод о выполнении задач урока.	Информация о домашнем задании, инструктаж по его выполнению		ОК 1, ОК 4. П1.
10. Рефлексия (подведение итогов занятия) , 5 мин
Акцентирует внимание на конечных результатах учебной деятельности обучающихся на занятии.	1. Проводят самоанализ: “Чему научились и что нового узнали?”	Осознание своей учебной деятельности; самооценка результатов деятельности своей.		ОК1, ПК 1, ПК4

2. Информационный блок

2.1. План лекции

№ п/п	Изучаемые вопросы	Уровень усвоения
1.	Устная работа. Повторение. Проверка домашнего задания.	1
2.	Объяснение темы Показательная функция, свойства и график.
	2. 1.Основные определения.	2
	2.2.Свойства показательной функции.	2
	2.3 График.
3.	Закрепление нового материала.
	3.1 Решение примеров устно 195,198 и 199.	3
	3.2 Решение задач на построение графиков показательной функции	3
	3.3 Примеры и разбор решения заданий тренировочного модуля.
4	Решение упражнений (нечетные пункты) на закрепление темы (№192-200)	3
5.	Домашнее задание № 192-200 (четные пункты).	3

2.2 Текст лекции

Показательная функция.

Перечень вопросов, рассматриваемых в теме:

- какая функция называется показательной;

- какие свойства имеет показательная функция в зависимости от ее основания;

- какой вид имеет график показательной функции в зависимости от ее основания;

- примеры реальных процессов, описываемых показательной функцией.

Теоретический материал.

1. Определение, свойства и график показательной функции

Определение: Функция вида y=а^х, a>0, а≠1 называется показательной функцией с основанием а.

Такое название она получила потому, что независимая переменная стоит в показателе. Основание а – заданное число.

Для положительного основания значение степени а^х можно найти для любого значения показателя х – и целого, и рационального, и иррационального, то есть для любого действительного значения.

Сформулируем основные свойства показательной функции.

1. Область определения.

Как мы уже сказали, степень а^х для a>0 определена для любого действительного значения переменной х, поэтому область определения показательной функции D_(y)=R.

2. Множество значений.

Так как основание степени положительно, то очевидно, что функция может принимать только положительные значения.

Множество значений показательной функции Е_(y)=R⁺, или Е_(y)=(0; +∞).

3. Корни (нули) функции.

Так как основание a>0, то ни при каких значениях переменной х функция не обращается в 0 и корней не имеет.

4. Монотонность.

При a>1 функция монотонно возрастает.

При 0<a<1 функция монотонно убывает.

5. При любом значении а значение функции y (0) = а⁰ =1.

6. Графики показательных функций изображены на рисунках:

1) для случая a>1:

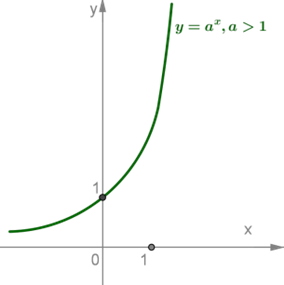
2) для случая 0<a<1:

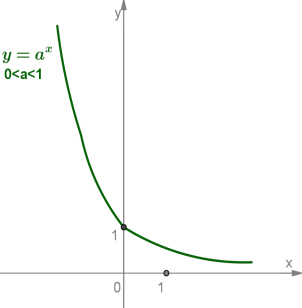
Построим графики функций y=2^x и y=(12)^x, использовав рассмотренные свойства и найдя несколько точек, принадлежащих графику.

Пример:

отметим, что график функции y=2x проходит через точку (0;1) и расположен выше оси Ox.

Если x<0 и убывает, то график быстро приближается к оси Ox (но не пересекает её);

если x>0 и возрастает, то график быстро поднимается вверх.

Такой вид имеет график любой функции y=ax, если a>1.

Пример:

График функции y=(1/2)x также проходит через точку (0;1) и расположен выше оси Ox.

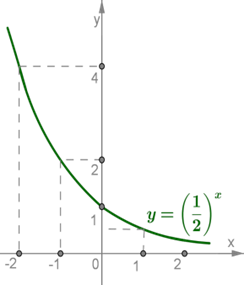
Если x>0 и возрастает, то график быстро приближается к оси Ox (не пересекая её);

если x<0 и убывает, то график быстро поднимается вверх.Такой же вид имеет график любой функции y=ax, если 0<a<1

Примеры и разбор решения заданий тренировочного модуля

Пример 1.

Выберите показательные функции, которые являются монотонно убывающими.

y=3^x-1
y=(0,4)^x+1
y=(0,7)^-х
y=
y=3^-2х
y=10^{2x +1}

Решение:

Монотонно убывающими являются показательные функции, основание которых положительно и меньше единицы. Такими функциями являются: 2) и 4) (независимо от того, что коэффициент в показателе функции 4) равен 0,5), заметим, что функцию 4) можно переписать в виде: 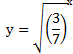, используя свойство степеней.

Также монотонно убывающей будет функция 5). Воспользуемся свойством степеней и представим ее в виде:

2) 4) 5)

Пример 2.

Найдите множество значений функции y=3^x+1– 3.

Решение:

Рассмотрим функцию.

Так как 3^x+1>0, то 3^x+1– 3>–3, то есть множество значений:

(– 3; +∞).

Пример 3.

Найдите множество значений функции y=|2^x– 2|

Рассмотрим функцию.

2^x–2>–2, но, так как мы рассматриваем модуль этого выражения, то получаем: |2^x– 2|0.

4. Решение задач № 192-200 (не четные)

5. Подведение итогов урока. Выставление оценок. Домашнее задание: выучить теоретический материал, № 192- 200 (четные).

2.3. Глоссарий

Термин	Значение
Монотонно возрастающая.	Это функция на промежутке <a; b>, если (чем больше аргумент, тем больше значение функции).
Показательная функция.	Это функция вида , a>0, а≠1 с основанием а.
Монотонно убывающая.	Это функция на промежутке <a; b>, если (чем больше аргумент, тем меньше значение функции).

3. Контролирующий блок

Вариант 1.

Тест по теме «Показательная функция»

1. Из приведенных ниже функций укажите показательную:

а) у=х³ б) в) г)

1) а и в

2) а и б

3) в и г

4) б и г

2. Из приведенных ниже утверждений верными являются:

а) функция принимает в некоторой точке значение 0;

б) функция является нечетной;

в) функция пересекает ось Оу в точке (0; 1);

г) функция принимает только положительные значения.

1) а и в

2) а и б

3) в и г

4) б и г

3. При каких значениях х выражении больше 1?

1) x>0

2) x<0

3) x>1

4) x<1

4. Областью значений функции является множество

5. Из приведенных ниже утверждений верными являются:

а) графики функций и симметричны относительно оси ординат;

б) графики функций и пересекают ось Оу в точке (0; 1);

в) графики функций и симметричны относительно оси абсцисс;

г) графики функций и пересекают ось Ох в точке (1; 0).

1) а и в

2) а и б

3) в и г

4) б и г

6. Из приведенных ниже функций укажите возрастающие:

а) б) в) г)

1) а и в

2) а и б

3) в и г

4) б и г

7. Корень уравнения равен

1) 1

2) 2

3) 3

4) 4

8. Выражение 2а, где а - корень уравнения , равно

1) 9

2) 11

3) -11

4) -9

9. Произведение корней уравнения равно

1) 19

2) -19

3) -24

4) -18

10. Наименьшее целое значение х, удовлетворяющее неравенству , равно

1) 0

2) -1

3) 1

4) не существует

Вариант 2.

Тест по теме «Показательная функция»

1. Из приведенных ниже функций укажите показательную:

а) у=х⁷ б) в) г)

1) а и в

2) а и б

3) в и г

4) б и г

2. Из приведенных ниже утверждений верными являются:

а) функция не принимает значение 0;

б) функция является четной;

в) функция пересекает ось Оу в точке (0; 1);

г) функция принимает только неотрицательные значения.

1) а и в

2) а и б

3) в и г

4) б и г

3. При каких значениях х выражении меньше 1?

1) x>0

2) x<0

3) x>1

4) x<1

4. Областью значений функции является множество

5. Из приведенных ниже утверждений верными являются:

а) графики функций и симметричны относительно оси ординат;

б) графики функций и не пересекают ось Ох;

в) графики функций и симметричны относительно оси абсцисс;

г) графики функций и пересекают ось Оу в разных точках.

1) а и в

2) а и б

3) в и г

4) б и г

6. Из приведенных ниже функций укажите убывающие:

а) б) в) г)

1) а и в

2) а и б

3) в и г

4) б и г

7. Корень уравнения равен

1) 1

2) 2

3) 3

4) 4

8. Произведение корней уравнения равна

1) 4

2) -12

3) 1

4) -2

9. Сумма корней уравнения равно

1) -37

2) 37

3) 1

4) -1

10. Наибольшее целое значение х, удовлетворяющее неравенству , равно

1) 2

2) 3

3) 0

4) не существует

Вариант 1.

Вариант 2.

1	2	3	4	5	6	7	8	9	10
4	3	1	2	2	2	4	3	3	1
4	1	2	2	4	2	4	3	3	4

Скачано с www.znanio.ru

Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.

Посмотрите также