помощью квадратных уравнений_Методические рекомендации (1)

Методические рекомендации к уроку:

Решение задач с помощью квадратных уравнений.

Цель обучения:

8.5.2.1 решать текстовые задачи с помощью квадратных уравнений.

Цели урока: Данный урок направлен на выработку навыков составления математических моделей текстовых задач и их решения с помощью квадратных уравнений.

Вид урока: урок-практикум.

Определение основных терминов:

В процессе решения задачи чётко выделяются три этапа математического моделирования:

• 1 этап - это перевод условий задачи на математический язык; при этом выделяются необходимые для решения данные и искомые и математическими способами описываются связи между ними;
• 2 этап - внутримодельное решение (то есть нахождение значения выражения, выполнение действий, решение уравнения);
• 3 этап - интерпретация, то есть перевод полученного решения на тот язык, на котором была сформулирована исходная задача.

Этапы урока:

       В самом начале урока учитель объявляет тему урока и совместно с учащимися определяет цели урока, «зону ближайшего развития» учащихся, критерии оценивания, а также знакомит учеников с этапами урока.   

     На этапе актуализации выполняется вспомогательное упражнение «Разминка», направленное на выработку умений составления простейших математических моделей текстовых задач. Учащиеся совместно с учителем выполняют типовые задачи, представленные на слайдах презентации. Учащиеся решают задачи, обсуждают решения и ответы, представляют альтернативные варианты решений, задают вопросы по алгоритмам выполнениязаданий. Данный вид работы поможет учащимся при дальнейшем составлении математических моделей и решении текстовых задач.

      Далее учащимся предлагается практикум по решению задач. Учащиеся  решают типовые задачи с помощью квадратных уравнений. Данный вид работ помогает формированию умений и навыков решения простейших задач. Работа в парах. Класс делится на пары, таким образом, чтобы сильный учащийся работал с менее подготовленным. Каждый учащийся самостоятельно в тетради решает задачи. Затем учащиеся в паре обмениваются тетрадями и проводят взаимооценивание (по предоставленным учителем ответам).  Учащиеся решают задания, устно комментируя решения. Учитель комментирует работу учащихся, помогает при необходимости, корректирует решения и ответы, предоставляет ученикам обратную связь.

Приложение №1.

    1. В прямоугольном треугольнике один катет больше другого на 7 см, а гипотенуза больше меньшего катета на 8 см. Найдите стороны треугольника.

 Решение: Пусть х см – длина меньшего катета, тогда

х² + (х + 7)² = (х + 8)².

Решим полученное уравнение  х² – 2х – 15 = 0, 

 х = - 3   - не удовлетворяет условию задачи. 

 х = 5 (см)   - меньший катет.  Тогда 5 + 7 = 12(см) – больший катет,

5 + 8 = 13(см) – гипотенуза.

Ответ: 5 см, 12 см и 13 см.

2. Найти два последовательных натуральных числа, произведение которых равно 210.

Уравнение: х(х+1)=210

Ответ: 14 и 15.

3. Несколько приятелей решили сыграть турнир по шахматам. Кто-то из них подсчитал, что если каждый сыграет с каждым по одной партии, то всего будет сыграно 36 партий. Сколько было приятелей?

Решение:
Пусть х приятелей участвует в турнире, тогда каждый из них сыграет (х – 1) партию, но в этом случае партия каждой пары учтена дважды, значит всего было сыграно 0,5х(х – 1) партий, что по условию задачи равно 36. Составим и решим уравнение:
0,5х(х– 1) = 36,
х(х – 1) = 72,
х² – х – 72 = 0,
D = 1 + 288 = 289,
х = ,
х₁ = 9,
х₂ = – 8 – не удовлетворяет условию задачи.

9 приятелей участвовало в турнире.

Ответ: 9 приятелей.

4. Периметр прямоугольника равен 46 смм, а его диагональ – 17 см. Найти стороны прямоугольника.

Ответ: 8 см и 15 см.

5. Произведение двух натуральных чисел, одно из которых на 5 больше другого, равно 104. Найдите эти числа.

Решение. Пусть х – меньшее из данных чисел, тогда (х + 5) – большее из данных чисел. По условию задачи х · (х + 5) = 104. Решим полученное уравнение  х² + 5х – 104 = 0,D = 441, х  = - 13   - не удовлетворяет условию задачи (натуральные числа); х = 8   - меньшее число. Тогда  8 + 5 = 13   - большее число.

Ответ: 8 и 13.

    Следующим этапом урока является решение прикладных задач.

   Решение прикладных задач с помощью квадратных уравнений – это один из наиболее важных моментов урока. Решение прикладных задач способствует развитию функциональной грамотности, критического мышления учащихся и повышает их мотивацию к изучению математики. Учащиеся выполняют прикладные задачи в тетрадях. Учитель наблюдает, помогает, комментирует решение. Затем показывает правильное решение на слайдах презентации.Учащиеся оценивают работу, исправляют ошибки, корректируют и обсуждают решения и ответы , задают вопросы по задачам. Учитель наблюдает, при необходимости корректирует и направляет, выявляет учащихся допускающих ошибки для планирования дальнейшей работы в классе и индивидуальной работы по коррекции знаний.

Приложение №2.

1. В море встретились два корабля. Один из них шел в восточном направлении, другой – в северном. Скорость первого на 10 узлов больше, чем второго. Через 2 часа расстояние между ними оказалось равным 100 милям. Найдите скорость каждого корабля.

Решение:

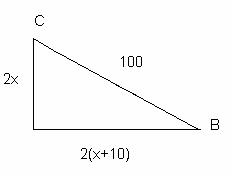
Пусть х узлов – скорость второго корабля, тогда (х – 10) узлов – скорость первого корабля, за 2 часа они пройдут 2х и 2(х –10) миль соответственно, т.к. они идут в перпендикулярных направлениях, то, используя теорему Пифагора, составим и решим уравнение:

(2х)² + (2(х + 10))² = 100²
4х² + 4(х² + 20х + 100) = 10000
2х² + 20х + 100 = 2500
х² + 10х + 50 – 1250 = 0
х² + 10х – 1200 = 0
= 25 + 1200 = 1225
х = – 5 + 35
х₁ = – 40 – не удовлетворяет смыслу задачи,
х₂ = 30
30 узлов – скорость корабля, идущего на север, тогда 30 + 10 = 40 (узлов) – скорость корабля, идущего на восток.

Ответ: 30 узлов и 40 узлов.

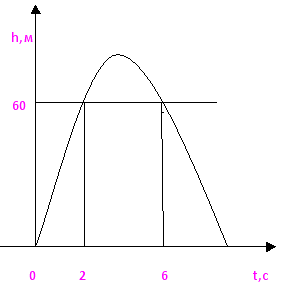
2. Тело брошено вертикально вверх с начальной скоростью 40м/с. Через сколько секунд оно окажется на высоте 60м?

Решение:  из курса физики известно, что если не учитывать сопротивление воздуха, то высота h(м), на которой брошенное вертикально вверх тело окажется через t(с), может быть найдена по формуле h=V₀ t-gt²/2, г де V₀(м/с) - начальная скорость, g - ускорение свободного падения, приближенно равно 10 м/с2.

60=40t-5t².

Отсюда 5t²-40t+60=0,    t²-8t+12=0.

Решив полученное уравнение, найдем, что t₁= 2, t₂ = 6. график зависимости h от t, где

h= 40t-5t². Из графика видно, что тело, брошенное вертикально вверх, в течение первых 4 с поднимается вверх до высоты 80м, а затем начинает падать. На высоте 60 м от земли оно оказывается дважды: через 2 с и через 6 с после броска. Условию задачи удовлетворяют оба найденных корня.

    В конце урока учитель просит учащихся подвести итоги, обратить внимание на то, что было трудно, выясняет причины затруднений.

Домашняя работа направлена на закрепление умений и навыков решения задач.