Построение и исследование физических моделей из курса физики. Проект «Бросание мячика в площадку»

Урок 39-40, 9 класс

Учитель: Брух Т.В.

Дата:_____________

Тема: «Построение и исследование физических моделей из курса физики. Проект «Бросание мячика в площадку»»

Цели  урока:

Общеобразовательные:

формирование умения исследования физических моделей графическим

методом и методом Подбор параметра;

Ознакомление со способами представления  моделирования и формализации;

умение описывать окружающую действительность с помощью

различных информационных объектов;

Развитие умений строить информационные модели различных объектов.

Воспитывающие:

Продолжение формирования и развития информационного видения окружающего мира;

формирование эмоционально-ценностного отношения к результатам

интеллектуального труда.

Развивающие:

овладение основными логическими приемами работы с базовыми

понятиями информатики;

овладение навыками представления объектов окружающей действительности.

Практические:

Умение применять полученные знания, используя программу Microsoft Excel.

Ход урока:

а) организационный момент

Здравствуйте, ребята.  Садитесь, пожалуйста.

Тема нашего урока «Построение и исследование физических моделей».

Сегодня, вы узнаете, как можно исследовать физические модели двумя методами:  графическим методом и методом Подбор параметра  с помощью Microsoft Excel.

б) актуализация  знаний

1. Какие бывают модели? Приведите примеры материальных и информационных моделей.

2. Что такое формализация? Приведите примеры формальных моделей.

3.  Какие вы можете назвать примеры моделирования в различных областях деятельности?

4. Может ли объект иметь несколько моделей? Если да, то приведите примеры.

5. Могут ли разные объекты описываться одной и той же моделью? Если да, то приведите примеры.

6.  Каковы основные этапы разработки и исследования моделей на компьютере?

7. Какие программные средства обычно используются для создания компьютерных моделей?

в) объяснение нового материала

Построение формальной модели движения тела, брошенного под углом к горизонту.

Задача: в процессе тренировок теннисистов используются автоматы по бросанию мячика в определенно место площадки. Необходимо задать автомату необходимую скорость и угол бросания мячика для попадания в мишень определенного размера, находящуюся на известном расстоянии.

Качественная описательная модель.

Из условия задачи можно сформулировать следующие основные  предположения:

-мячик мал по сравнению с Землей, поэтому его можно считать материальной точкой;

-изменение высоты мячика мало, поэтому ускорение свободного падения можно считать постоянной величиной     g = 9,8 м/с , следовательно, движение по оси OУ можно считать равноускоренным;

-скорость бросания мячика мала, поэтому сопротивлением воздуха можно пренебречь, следовательно, движение по оси OХ можно считать равномерным.

Формальная модель

Для формализации модели обозначим величины:

-начальную скорость мячика – v0;

-угол бросания мячика - α ;

-высоту стенки - h;

-расстояние до стенки -s.

Используем известные из курса физики формулы  равномерного и равноускоренного движения для определения координат мячика. Дальность x и высоту y при заданной начальной скорости v0 и угле бросания α для любого момента времени t можно вычислить по следующим формулам:

x= v0 * cos α * t,     y= v0*sin α * t - g * t2 / 2

Чтобы определить, попадет ли мячик в стенку, необходимо вычислить его координату у в момент времени, когда он будет находиться на расстоянии s. Из первой формулы выражаем время, которое понадобится мячику, чтобы преодолеть расстояние s:                   t = s / (v0*cos α).

Подставляем это значение времени t в формулу для вычисления координаты  y. Получаем  t - высоту мячика над землей на расстоянии s:

                                                    l = s * tg α-g * s2 / (2* v02* cos2 α).

Формализуем теперь условие попадания мячика в мишень. Попадание произойдет, если значение высоты мячика  l будет удовлетворять условию в форме неравенства: 0     l    h.Если   l < 0, то это обозначает «недолет». А если  l > h , то это означает «перелет».

1.Для ввода начальной скорости будем использовать ячейку В1, а для ввода угла – ячейку В2.

2. Введем в ячейки А5:А18 значения времени с интервалом 0,2 с. 3. В ячейки В5 и С5 введем формулы:

=$B$1*COS(РАДИАНЫ($B$2))*A5

=$B$1*SIN(РАДИАНЫ($B$2))*A5-4,9*A5*A5

4. Скопируем формулы в ячейки В6:В18 и С6:С18 соответственно.

Визуализируем модель, построив график зависимости

координаты у от координаты х (траекторию движения тела).

5. Построить диаграмму типа График, в которой используется в качестве категории диапазон ячеек С5:С18.

Исследуем модель и определим с заданной точностью 0,10 диапазон изменений угла, который обеспечивает попадание в мишень, находящуюся на расстоянии 30 м и имеющую высоту 1 м, при заданной начальной скорости 18 м/с. Воспользуемся

для этого методом Подбор параметра.

6.Установить для ячеек точность один знак после запятой.

7.Внести в ячейки В21, В22 и В23 значения расстояния до мишени      = 30м, начальной скорости   =18 м/с и угла   = 35 ,

а в ячейку В25 – формулу для вычисления высоты мячика над

поверхностью для заданных начальных условий:

=$B$21*TAN(РАДИАНЫ(В23)) – (9,81*В21^2)/(2*B22^2*COS(РАДИАНЫ(В23))^2)

Для заданных начальных условий определим углы, которые обеспечивают попадание в мишень на высотах 0 и 1 м.

8. Выделить ячейки В25 и ввести команду (Сервис-Подбор параметра). На появившейся диалоговой панели ввести в поле Значение: наименьшую высоту попадания в мишень (0). В поле Изменяя ячейки: ввести адрес ячейки, содержащей значение угла  (в данном случае $B$23).

9. В ячейке В23 появится значение 32,6. Повторить процедуру подбора параметра для максимальной высоты попадания в мишень – в ячейке В23 получится число 36,1.

Таким образом, исследование компьютерной модели в электронных таблицах показало, что существует диапазон значений угла бросания от 32,6 до 36,1 , который обеспечивает попадание в мишень высотой 1 м, находящуюся на расстоянии 30 м, мячиком, брошенным со скоростью 18 м/с.

г) закрепление знаний

Задача:

Тело брошено вертикально вверх с некоторой высоты. Определить через какое количество времени тело упадет на поверхность земли.

(построение и исследование физической модели проводится учащимися самостоятельно).

По завершению учащиеся демонстрируют полученные результаты.

Качественная описательная модель.

Если начальная скорость бросания тела v0 существенно меньше первой космической скорости и высота бросания   h , существенно меньше радиуса Земли, можно использовать модель, рассмотренную ранее.

Формализованная модель.

Движение по вертикали – равноускоренное, поэтому изменение координаты у в зависимости от времени описывается с помощью формулы:

   y = h0 + v0 * t – g * t2 / 2

1.Ввести начальные значения высоты  h0  и скорости  v0 в ячейки В1 и В2 соответственно.

2. Создадим таблицу значений зависимости координаты от времени. Введем в ячейки А5:А18 значения моментов времени  t  (в секундах) от 0 до 2,6 с шагом 0,2 с.

3. В ячейки В5 введем формулу уравнения движения: =$B$2+$B$3*A5-4,9*A5^2, в которой использованы абсолютные ссылки на ячейки, содержащие начальные условия.

4. Скопируем формулы в ячейки В6:В18.

5. Построить диаграмму типа График, в которой используется в качестве категории диапазон ячеек В5:В18.

Точка пересечения графика с осью  t соответствует времени падения тела (примерно 2,4с).

д) подведение итогов урока:

Итак, ребята, сегодня вы научились исследовать физические модели двумя методами средствами  Microsoft Excel. Такое же исследование можно провести, используя язык Visual Basic.

(работы учащихся оцениваются по пятибалльной шкале).

е) домашнее задание:

Проект «Бросание мячика в площадку» в электронных таблицах Microsoft Excel

 Аппаратное и программное обеспечение. Компьютер с установленной операционной системой  Windows или  Linux.

 Цель работы. Научиться создавать компьютерные модели движения в электронных таблицах и на языке объектно-ориентированного программирования Visual Basic.

 Задание. Разработать проект, в котором визуализируется траектория движения тела, брошенного под углом к горизонту, и выясняется, попадет ли тело в площадку определенной длины, находящуюся на заданном расстоянии.

Задание. Проект «Бросание мячика в площадку» в электронных таблицах Microsoft Excel 

1. В операционной системе  Windows запустить электронные таблицы Microsoft Excel командой [Пуск - Все программы - Microsoft Office - Microsoft Excel]

Построение траектории движения мячика.

Для ввода начальной скорости и0 бросания мячика будем использовать ячейку В1, а для ввода угла бросания — ячейку В2.

Введем в ячейки А5:А18 значения времени t с интервалом 0,2 с, и вычислим по формулам (2.1) значения координат тела х и y для заданных значений времени.

2. Ввести:

• в ячейку В5 формулу =$В$1*С08(РАДИАНЫ($В$2))*А5;

• в ячейку С5 формулу =$В$1*8Ш(РАДИАНЫ($В$2))*А5-4,9*А5*А5

В электронных таблицах аргументы функций COS() и SIN() задаются в радианах, поэтому необходимо преобразовать значения углов из градусов в радианы с помощью функции РАДИАНЫ().

3. Скопировать введенные формулы в ячейки В6:В18 и С6:С18 соответственно.

Получим в столбце В значения координаты мячика по оси X, а в столбце С — координаты по оси Y, вычисленные для определенных моментов времени.

Координаты мячика в заданные моменты времени

Визуализируем модель, построив график зависимости координаты y от координаты х (траекторию движения тела). Для построения траектории движения мячика используем диаграмму типа График.

4. При построении графика в качестве категорий использовать диапазон ячеек В5:В18, а в качестве значений — диапазон ячеек С5:С18.

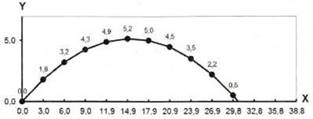Траектория движения мячика

5. По полученному графику (траектории движения мячика) можно качественно судить, попадет ли он в площадку при заданных начальных условиях (расстоянии до площадки и ее длины).