Практическая работа

Использование компьютерных моделей различных процессов Цель работы: 

 изучить информационные модели в виде таблицы, графа, дерева;   научиться решать задачи поиска данных в базе данных, представленной в табличном виде;  научиться строить графы, определять количество путей с использованием графов и таблиц.

Краткие теоретические сведения

Структурирование информации  это установление главных элементов в информационных сообщениях и установление связей между ними. Структурирование выполняется с целью облегчения восприятия и поиска информации. Структурирование возможно при помощи следующих структур (информационных моделей): множество, линейный список, дерево, граф, таблица.

Граф – набор вершин и связей между ними. Точки – это вершины графа, линии – ребра. Графы используют для структурирования информации, если «взаимоотношения» между объектами сложные. Связный граф – это граф, между любыми вершинами которого существует путь. Граф называется древовидным, если для  каждой пары вершин существует только одно соединяющее ребро. У взвешенных графов указан «вес ребра» его числовое значение. Из взвешенных графов получается весовая матрица.

Примеры решения задач

Пример 1. Представлены две таблицы из базы данных. Каждая строка Таблицы 2 содержит информацию о ребенке и об одном из его родителей. Информация представлена значением поля ID в соответствующей строке Таблицы 1. Определите на основании приведенных данных суммарное количество прямых потомков (т.е. детей, внуков, правнуков) Иоли А.Б.

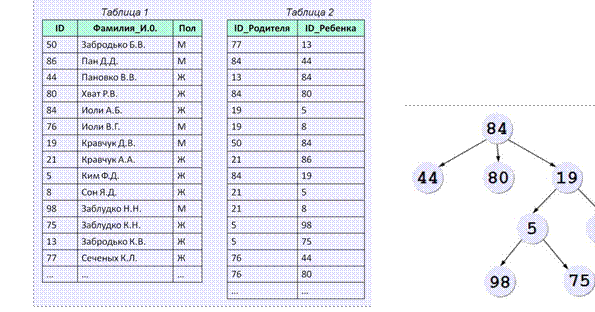
Решение:

1)      В первой таблице находим Иоли А.Б, ей соответствует ID  84

2)      Все остальное решение будет связано со второй таблицей: будем в ней искать ID родителя и соответствующего ему ID ребенка.

3)      Выполним задание при помощи дерева, подробно рассматривая каждый уровень иерархии: сначала детей родителя 84, затем по полученным ID  найдем внуков Иоли А.Б, затем правнуков и т.д. 4) Посчитаем общее количество потомков: 7.

Ответ: 7 прямых потомков.

Пример 2. Между населенными пунктами A, B, C, D, E, F построены дороги, протяженность которых  приведена в таблице. Передвигаться можно только по дорогам, указанным в таблице. Определите длину кратчайшего пути между пунктами A и F.

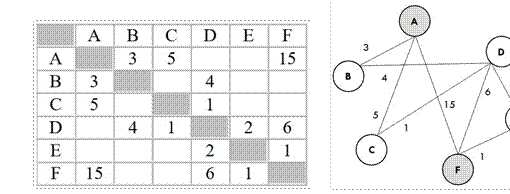
Решение:

1)      Построим граф: точками A, B, C, D, E, F, расположенными по кругу, обозначим населенные пункты. 

2)      Если в таблице есть число, соединяем точки отрезком и подписываем сверху это число. 

3)      Отмечаем конечный пункт (в нашем случае это F) и рассматриваем пункты, из которых можно в него попасть (в нашем случае это A, E, D). В свою очередь в пункт E можно попасть из D, а в пункт D – из C и B. В пункты C и B попадаем из A. Получили начальный пункт. Изобразим дерево всех возможных путей из A в F. 

4)      Вычислим длины полученных дорог. 

5)      AF=15, ACDEF=5+1+2+1=9, ABDEF=3+4+2+1=10, ACDF=5+1+6=12, ABDF=3+4+6=13.

6)      Выбираем длину кратчайшего пути  – 9.

Ответ: 9 - длина кратчайшего пути между пунктами A и F.

Пример 3. На рисунке представлена схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, И, К. По каждой дороге можно двигаться только в одном  направлении, указанном стрелкой. Сколько существует  различных путей из города А в город К?

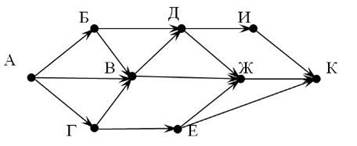
Решение: Подсчитаем количество путей, последовательно для каждой из вершин графа. Заполним таблицу:

Ответ: 10 различных путей.

ВАРИАНТ 1

ЗАДАЧА 1. Представлены две таблицы из базы данных, в которых собраны сведения о сотрудниках некоторой организации. Каждая строка Таблицы 2 содержит информацию о сотруднике структурного подразделения и о его непосредственном руководителе, который, в свою очередь, является непосредственным подчиненным руководителя более высокого уровня. Информация представлена значением поля ID в соответствующей строке Таблицы 1. Определите на основании приведенных данных суммарное количество подчиненных (непосредственных и через руководителей более низкого уровня) Сидорова Т.И.

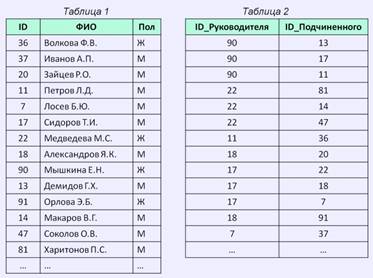
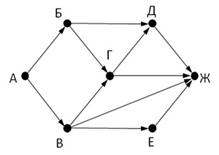
ЗАДАЧА 2. На рисунке изображена схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город Ж?

ЗАДАЧА 3. На рисунке приведена весовая матрица графа. Постройте граф и определите, сколько рёбер имеет такой граф и суммарный вес всех ребер графа.

ВАРИАНТ 2

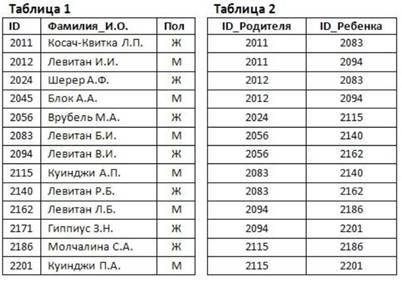
ЗАДАЧА 1. Представлены две таблицы из базы данных. Фрагмент базы данных содержит сведения о родственных отношениях. Информация представлена значением поля ID в соответствующей строке  Определите на основании приведенных данных, сколько всего внуков и внучек есть у Левитана И.И.

ЗАДАЧА 2. На рисунке представлена схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З, И. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город И? 

ЗАДАЧА 3. На рисунке приведена весовая матрица графа. Постройте граф и определите, сколько рёбер имеет такой граф и суммарный вес всех ребер графа.

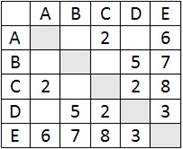
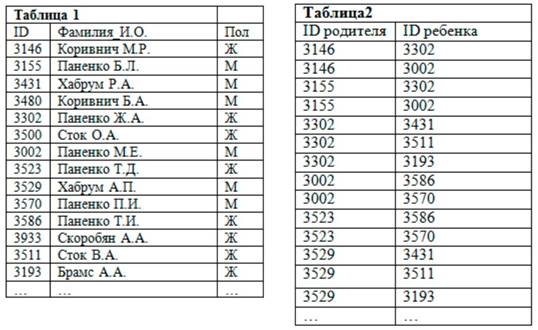
ВАРИАНТ 3 ЗАДАЧА 1. В фрагменте базы данных представлены сведения о родственных отношениях. На основании приведённых данных определите. Сколько внуков у Паненко Б.Л. упомянуты в таблице 1.

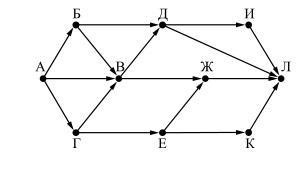
ЗАДАЧА 2. На рисунке представлена схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, И, К, Л. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город Л?

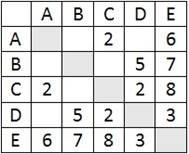
ЗАДАЧА 3. На рисунке приведена весовая матрица графа. Постройте граф и определите, сколько рёбер имеет такой граф и вес ребра, соединяющего вершины C и E.