
Практическая работа: Построение сечений
Критерии оценивания: за первую задачу 5 баллов (по баллу за каждую правильную линию, 1 балл за описание построения, 1 балл за штриховку сечения), вторая задача - 7 баллов (по одному баллу за каждую линию, 2 балла за описание построения и 1 балл за штриховку), третья задача – 8 баллов (по одному баллу за каждую линию, балл за построение следа, 2 балла за описание построения и 1 балл за штриховку). Максимальный балл за работу 20 баллов.
|
0 – 9 баллов |
«2» |
|
10 – 14 баллов |
«3» |
|
15 – 18 баллов |
«4» |
|
19 – 20 баллов |
«5» |
|
|
Задача 1. Построить сечение параллелепипеда плоскостью, проходящей через точки A, B и C.
|
|
|
Задача 2. Построить сечение параллелепипеда плоскостью, проходящей через точки Z, D и Y, используя свойство параллельных плоскостей.
|
|
|
Задача 3. Построить сечение параллелепипеда плоскостью, проходящей через точки Z, D и Y, используя метод следов.
|
|
|
Задача 1. Построить сечение тетраэдра плоскостью, проходящей через точки A, B и L.
|
|
|
Задача 2. Построить сечение параллелепипеда плоскостью, проходящей через точки Z, M и X, используя свойство параллельных плоскостей.
|
|
|
Задача 3. Построить сечение параллелепипеда плоскостью, проходящей через точки Z, M и X, используя метод следов.
|
Построить сечение многогранника плоскостью – это значит указать точки пересечения секущей плоскости с ребрами многогранника и соединить эти точки отрезками, принадлежащими граням многогранника.
Для построения сечения многогранника плоскостью нужно в плоскости каждой грани указать 2 точки, принадлежащие сечению, соединить их прямой и найти точки пересечения этой прямой с ребрами многогранника.
При построении сечения
многогранника мы получаем плоскую фигуру, имеющую следующее количество сторон:
от треугольника до ![]() сторон. Так у тетраэдра 4 грани, значит в
сечении может быть треугольник и четырехугольник. У параллелепипеда 6 граней,
следовательно, в сечении могут быть треугольники, четырехугольники,
пятиугольники и шестиугольники.
сторон. Так у тетраэдра 4 грани, значит в
сечении может быть треугольник и четырехугольник. У параллелепипеда 6 граней,
следовательно, в сечении могут быть треугольники, четырехугольники,
пятиугольники и шестиугольники.
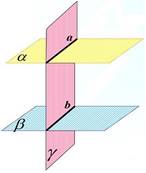 Используем для построения
сечений свойство параллельных плоскостей: если две параллельные плоскости
пересечены третьей, то линии их пересечения параллельны.
Используем для построения
сечений свойство параллельных плоскостей: если две параллельные плоскости
пересечены третьей, то линии их пересечения параллельны.
Если в параллелепипеде на одной из граней проведена линия, по которой плоскость сечения пересекает грань, а на параллельной ей грани есть точка, принадлежащая сечению, то через эту точку можно провести линию параллельную линии сечения.
Линия пересечения плоскости сечения и плоскости грани многогранника называется следом секущей плоскости на плоскости этой грани многогранника. Точка пересечения плоскости сечения и прямой, содержащей ребро многогранника, называется следом секущей плоскости на прямой, содержащей это ребро многогранника.
Задача 1. Построить сечение параллелепипеда плоскостью, проходящей через точки К, H и N.
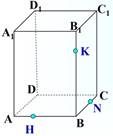
Решение. Точки H и К лежат на одной грани ![]() ,
следовательно их можно соединить. Точки К и N лежат на одной
грани
,
следовательно их можно соединить. Точки К и N лежат на одной
грани ![]() , следовательно их можно соединить. Точки N
и H лежат на одной грани
, следовательно их можно соединить. Точки N
и H лежат на одной грани ![]() , следовательно их можно соединить. Три
точки однозначно определяют плоскость.
, следовательно их можно соединить. Три
точки однозначно определяют плоскость.
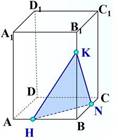 Построение: 1) HК
Построение: 1) HК
2) КN
3) NH
![]() –
искомое сечение
–
искомое сечение
Задача 2. Построить сечение тетраэдра плоскостью, проходящей через точки О, M и P.
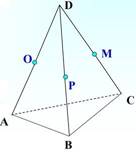
Решение. Точки O и P
лежат на одной грани ![]() , следовательно их можно соединить. Точки P
и M лежат на одной грани
, следовательно их можно соединить. Точки P
и M лежат на одной грани ![]() , следовательно их можно соединить. Точки M
и O лежат на одной грани
, следовательно их можно соединить. Точки M
и O лежат на одной грани ![]() , следовательно их можно соединить. Три
точки однозначно определяют плоскость.
, следовательно их можно соединить. Три
точки однозначно определяют плоскость.
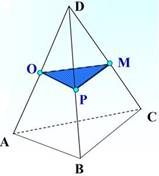 Построение: 1) OP
Построение: 1) OP
2) PM
3) MO
![]() –
искомое сечение
–
искомое сечение
Задача 3. Построить сечение параллелепипеда плоскостью, проходящей через точки К, H и N.
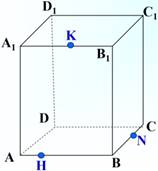
Решение. Точки H и К
лежат на одной грани ![]() , следовательно их можно соединить. Точки H
и N лежат на одной грани
, следовательно их можно соединить. Точки H
и N лежат на одной грани ![]() , следовательно их можно соединить. А вот
точки К и N соединять нельзя, так как они не принадлежат одной
грани. Если мы проведем прямую HN в плоскости грани
, следовательно их можно соединить. А вот
точки К и N соединять нельзя, так как они не принадлежат одной
грани. Если мы проведем прямую HN в плоскости грани ![]() , то мы
увидим, что в параллельной ей плоскости
, то мы
увидим, что в параллельной ей плоскости ![]() есть точка К, значит
по свойству параллельных плоскостей мы можем через точку К провести
прямую параллельную прямой HN. Эта прямая пересекется с ребром
есть точка К, значит
по свойству параллельных плоскостей мы можем через точку К провести
прямую параллельную прямой HN. Эта прямая пересекется с ребром ![]() в
некоторой точке, назовем ее О. Тогда точки О и N будут
принадлежать одной грани
в
некоторой точке, назовем ее О. Тогда точки О и N будут
принадлежать одной грани ![]() и их можно соединять.
и их можно соединять.
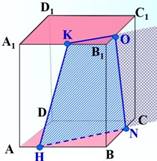
![]()
![]() Построение:
Построение:
1) HK
2) HN
3)
4) ![]()
5)
![]() –
искомое сечение
–
искомое сечение
Задача 4. Построить сечение параллелепипеда плоскостью, проходящей через точки К, H и N, используя метод следов.
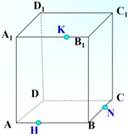
Решение. Точки H и К
лежат на одной грани ![]() , следовательно их можно соединить. Точки H
и N лежат на одной грани
, следовательно их можно соединить. Точки H
и N лежат на одной грани ![]() , следовательно их можно соединить. А вот
точки К и N соединять нельзя, так как они не принадлежат одной
грани.
, следовательно их можно соединить. А вот
точки К и N соединять нельзя, так как они не принадлежат одной
грани.
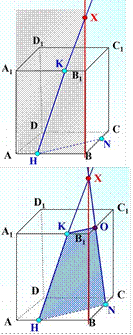
![]()
![]() Используем
метод следов. Прямая HК лежит на грани
Используем
метод следов. Прямая HК лежит на грани ![]() . Точка N – лежит
на грани
. Точка N – лежит
на грани ![]() . Эти грани имеют общую прямую
. Эти грани имеют общую прямую ![]() .
Поэтому, продолжим прямые HК и
.
Поэтому, продолжим прямые HК и ![]() до пересечения в
некоторой точке, например Х. Эта точка лежит на прямой
до пересечения в
некоторой точке, например Х. Эта точка лежит на прямой ![]() ,
следовательно, принадлежит плоскости грани
,
следовательно, принадлежит плоскости грани ![]() , значит на этой
плоскости у нас есть две точки Х и N – их можно соединить. Тогда
прямая ХN пересекется с ребром
, значит на этой
плоскости у нас есть две точки Х и N – их можно соединить. Тогда
прямая ХN пересекется с ребром ![]() в некоторой точке, например, точке О, которую
можно будет соединять с точкой К. Итоговое построение будет выглядеть
так:
в некоторой точке, например, точке О, которую
можно будет соединять с точкой К. Итоговое построение будет выглядеть
так:
Построение:
1) HK
2) HN
3)
4)
5)
6) KO
![]() – искомое сечение
– искомое сечение
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.