Практическая работа "Решение основных геодезических задач и задач по определению планового положения точек местности"

Занятие 32  Практическое занятие 6

Тема: Решение основных геодезических задач и задач по определению планового положения точек местности

Цель: Закрепить учебный материал  при решении задач.

Последовательность выполнения:

1. Информация для повторения и методические указания для выполнения :

При переходе от измеряемых линейно-угловых величин к координатам точек местности необходимо решить несколько геодезических задач.

1.1 Вычисление дирекционных углов направлений.

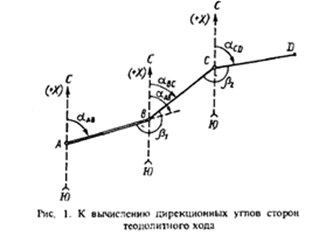
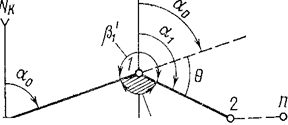
 α₁= α_о + 180⁰- β₁ ;  α₁= α_о - 180⁰ + β₁´

В этих формулах β₁ - правый, β₁´- левый по ходу углы, если считать, что ход направлен в сторону возрастания номеров вершин. Чаще всего принято измерять правые углы хода.

Решение треугольников. Для определения расстояний и уг­лов, которые невозможно или нецелесообразно измерять непо­средственно на местности, прибегают к построениям в виде треугольников. В них измеряют не менее трех линейных и угло­вых элементов, по которым, вычисляют остальные. Рассмотрим следующие типичные случаи.

Геодезическая задача – математического вида задача, связаная с определением взаимного положения точек земной поверхности и подразделяется на прямую и обратную задачу.

Прямой геодезической задачей (ПГЗ) называют вычисление геодезических координат - широты и долготы некоторой точки, лежащей на земном эллипсоиде, по координатам другой точки и по известным длине и дирекционному углу данного направления, соединяющей эти точки.

Обратная геодезическая задача (ОГЗ) заключается в определении по геодезическим координатам двух точек на земном эллипсоиде длины и дирекционного угла направления между этими точками.

1.2 Прямая геодезическая задача

В геодезии часто приходится передавать координаты с одной точки на другую. Например, зная исходные координаты точки А горизонтальное расстояние S_AB от неё до точки В и направление линии, соединяющей обе точки (дирекционный угол α_AB или румб r_AB), можно определить координаты точки В. В такой постановке передача координат называется прямой геодезической задачей.

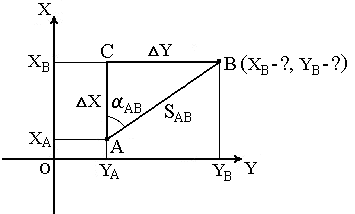
 Прямая геодезическая задача

Для точек, расположенных на сфероиде, решение данной задачи представляет значительные трудности. Для точек на плоскости она решается следующим образом.

Дано: Точка А( X_A, Y_A ), S_AB и α_AB.

Найти: точку В( X_B, Y_B ).

Непосредственно из рисунка имеем:

 ΔX = X_B – X_A ;

 ΔY = Y_B – Y_A .

Разности ΔX и ΔY координат точек последующей и предыдущей называются приращениями координат. Они представляют собой проекции отрезка АВ на соответствующие оси координат. Их значения находим из прямоугольного прямоугольника АВС:

ΔX = S_AB · cos α_AB ;

ΔY = S_AB · sin α_AB .

Так как в этих формулах S_AB всегда число положительное, то знаки приращений координат ΔX  и  ΔY зависят от знаков cos α_AB  и  sin α_AB. Для различных значений углов знаки ΔX и ΔY представлены в табл.1.

                Таблица 1-Знаки приращений координат ΔX и ΔY

При помощи румба приращения координат вычисляют по формулам:

ΔX = S_AB · cos r_AB ;

ΔY = S_AB · sin r_AB .

Знаки приращениям дают в зависимости от названия румба.

Вычислив приращения координат, находим искомые координаты другой точки:

 X_B = X_A + ΔX  ;

 Y_B = Y_A + ΔY  .

Таким образом можно найти координаты любого числа точек по правилу: координаты последующей точки равны координатам предыдущей точки плюс соответствующие приращения.

1.3 Обратная геодезическая задача

Обратная геодезическая задача заключается в том, что при известных координатах точек А( X_A, Y_A ) и В( X_B, Y_B ) необходимо найти длину S_AB и направление линии АВ: румб r_AB  и  дирекционный угол α_AB (рис.24).

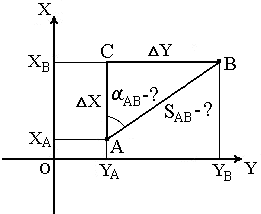
 Обратная геодезическая задача

Даннная задача решается следующим образом.

Сначала находим приращения координат:

 ΔX = X_B – X_A ;

 ΔY = Y_B – Y_A .

Величину угла r_AB определем из отношения

 .

По знакам приращений координат вычисляют четверть, в которой располагается румб, и его название. Используя зависимость между дирекционными углами      ( азимутами А) и румбами, находим α_AB.

Зависимость между дирекционными углами и румбами

Для контроля расстояние S_AB дважды вычисляют по формулам:

1.

2.

Расстояние S_AB можно определить также по формуле

.

2.     Задание:

1 вариант:               1)   α_1-2 = 234^о23^/

                                       β ₂ =  156^о17^/

                                       ______________    

                                           α _2-3 =  ?

                                  2)   х₁ = + 50,63 м

                                          у₁  = - 105,70 м

                                          r_1-2 = ЮЗ : 56^о13^/

                                          S_1-2 = 120,75

                                     ________________

                                            х₂ =?     у₂ = ?

 3)   х₁ = + 306,17 м

                                           у₁  = - 18,65 м

        х₂ = + 78,26 м

                                           у₂  = + 2,98 м

                                          _________________

                                            r_1-2 = ?       S_{1- 2} = ?                               

2 вариант:                  1)   α_{3 - 4}= 15^о06^/

                                          β ₄ =  80^о50^/

                                       ______________    

                                           α _4-5 =?

2)   х₁ = - 100,75 м

                                          у₁  = - 105,90 м

                                          r = СВ : 10^о40^/

                                          S = 19,88м

                                     ________________

                                            х₂ =?     у₂ =?

 3)   х₁ = + 17,45 м

                                           у₁  = + 6,99 м

        х₂ = - 30,85 м

                                           у₂  = + 100,12 м

                                          _________________

                                            r_1-2 = ?       S_{1- 2} = ?                               

Источники информации:

 Киселев М.И. Геодезия: учебник для студ. учреждений СПО/ М.И. Киселев, Д.Ш. Михелев. – 14-е изд. стер. – М.: Издательский центр «Академия», 2018.  стр. 17-18 (стр.42-51.)

Пояснение к выполнению практического задания (решение задач) –

Варианты для выполнения РЕШЕНИЯ ЗАДАЧ:

1 вариант 

ВЫПОЛНЯЮТ СТУДЕНТЫ ГРУППЫ АНАНЬЕВОЙ Н,И, (по осенней практике)

2 вариант

ВЫПОЛНЯЮТ СТУДЕНТЫ ПОДГРУППЫ ГУРИНА Р,В, (по осенней практике)

Дополнительное задание:

Выполненые задания в читаемом виде высылать на anivof@mail.ru

Скачано с www.znanio.ru