«Применение интеграла»

      Урок на тему: «Применение интеграла»

                                                        в классе 11

Цели урока:

1. Повторить, обобщить и систематизировать понятия первообразной и интеграла, формулы вычисления площади криволинейной трапеции.
2. Совершенствовать вычислительные навыки, развитие логического мышления, навыков использования интерактивно оборудования,
3. Продолжить воспитание патриотизма, чувства гордости за свою Родину, чувства ответственности за свои решения.

Тип урока: обобщающий урок

Структура урока:

1. Орг.момент — 3 мин
2. Актуализация знаний — 7 мин
3. Практическая работа — 12 мин
4. Физминутка (+историческая справка) — 3 мин
5. Работа в группах — 10 мин
6. Тестирование — 3 мин
7. Рефлексия — 3 мин
8. Сообщение домашнего задания — 4 мин

Ход урока:

1. Орг.момент

Добрый день, ребята! У нас сегодня на уроке присутствуют гости, которые вместе с нами будут познавать, где находит свое применение интеграл.

Мы начинаем урок.

Чтобы урок наш начался с отличным позитивным настроением, предлагаю вам посмотреть следующую картинку. Посмотрите внимательно на этот рисунок. Рисунок необычный, он составлен из математических знаков, геометрических фигур. Присмотритесь, пожалуйста. Вам нужно увидеть каких фигур или знаков большее количество? А теперь давайте исходя из этого рисунка, сформулируем тему нашего урока. («Интеграл») — открываем тетради, записываем число и тему урока.

Главная задача урока — показать свои знания, умения, которые вы приобрели в ходе изучения
темы «Интеграл». Хочу отметить, что задания на данную тему очень часто встречаются на ЕНТ, а также на государственных экзаменах по математике.

2. Актуализация знаний

В начале урока давайте проведем тест, по итогам которого вы увидите, какие формулы необходимо еще отработать, а что вы уже знаете отлично. (флипчарт № 1).

1. Вычисли интеграл:

1. 1/2 2. 1 3. 0

2. Запишите площадь заштрихованной фигуры как сумму или разность площадей криволинейных трапеций (Рисунок 1) — 0,5 мин

3. Запишите в виде определенного интеграла площадь фигуры, ограниченной линиями y=x2+1, x=1, x=2, y=0 — 1 мин

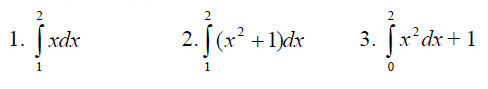
4.Вычислите площадь фигуры, ограниченной линиями y=x, y=0, x=3 — 1,5 мин

1. 3 2. 4,5 3. 1

5.Вычислите площадь фигуры, ограниченной линиями y=2x, y=0, x=a, x=b, a>0, b>a — 1,5 мин

1. 2(a-b) 2. 2 3. b2-a2

Тест выполняется при помощи тестирующих устройств ActiVot

Итог: кто ответил на все вопросы правильно? У кого 1 ошибка? У кого две ошибки?

3. Практическая работа — дифференцированно

Практическая работа основана на результатах тестирования в начале урока. Если ученики ошиблись в задании, то они решают примеры, аналогичные этому заданию. Примеры записаны по принципу «от легкого к сложному». Первые 3 заданий — это минимум, который должен знать ученик. Далее следуют задания с более высоким уровнем сложности.

Если ученики не допустили ни одной ошибки в тестировании, они имеют возможность получить дополнительную оценку, решив № 3–5 задания из списка.

4. Физминутка

Презентация «Артем» (+музыкальное сопровождение «Anthony Marc — When I Dream At Night»

Назаров Артем: Символ ∫ydx был введен немецким математиком Готфридом Лейбницем в 1686 году. Существует версия о том, что он букву S, используемую для обозначения суммы писал слегка удлиненной. Так постепенно и родился новый символ. Термин интеграл (от латинского integer-целый) был предложен в 1696 году учеником Лейбница — Иоганном Бернулли. Лейбниц, хотя и неохотно согласился с этим — в ходе выступления, учащиеся просматривают презентацию. Каждый следит за движениями фигур, тем самым происходит зарядка для глаз.

Физминутка: Учитель предлагает детям закрыть глаза и представить перед собой большой белый экран. Необходимо мысленно раскрасить этот экран поочередно любым цветом: например, сначала желтым, потом оранжевым, зеленым, синим, но закончить раскрашивание нужно самым любимым цветом.

5. Работа в группах — дифференцированно

1 группа — технологи производственного питания — Назаров А., Блинов А., Емельянов С., Егимбаев М., Саврулин А. (флипчарт № 2)

Работа команд над практическим заданием «Объем фрукта?». Тихо звучит классическая музыка, создающая ситуацию комфорта. Учащиеся, используя метод «исчерпывания» Архимеда, находят объем фрукта или овоща (режут лимон или апельсин на дольки), делают соответствующие записи в тетрадях.

2 группа: математики-исследователи — Аженева Н., Оралханова Ж., Моргунова Л., Киселева Т., Власова К.

Вывести формулу вычисления объема конуса.

Дополнительная задача: Стальной конус, имеющий в диаметре 25 см и высоту 30 см, стачивается до 20 см в диаметре, причем остается та же высота. На сколько уменьшится объём конуса?

5. Тестирование

Проверка формул: при помощи тестирующих устройств ACTIVot (флипчарт № 3) Верна ли формула:

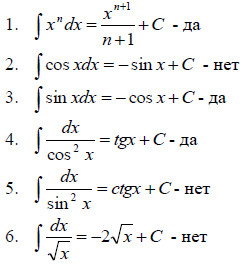
7. Рефлексия

Презентация-клип музыкальной группы «Интеграл». Оралханова Ж. (+музыкальное сопровождение песня группы «Интеграл» — Привет)

8. Сообщение домашнего задания

Учащиеся делают выводы по уроку.

Учитель предлагает учащимся провести сравнение результатов сегодняшнего урока и наступающим праздником — 20-летием Независимости РК. Каждое наше достижение, каждый вот такой урок — это наша маленькая победа, это вершина, которую мы сегодня преодолели. И вот из таких маленьких побед каждого гражданина нашей Родины складываются вершины Независимости.

Как вы думаете, где находит применение интеграл? А зачем обычному среднестатистическому человеку нужен интеграл? Все ли мы используем знания, полученные на уроке, где-то в повседневной жизни или в ближайшем будущем? Поднимите руки, у кого дома есть телевизор; у кого есть сотовый телефон; у кого дома есть компьютер. Так вот даже обычный сельский житель, который не имеет общего с наукой, в повседневной жизни пользуется знаниями об интеграле. Естественно, некоторые люди, которые пользуются этими приборами, могут и не знать, как вычисляется интеграл и что это вообще такое. Но каждый из нас пользуется предметами быта, даже не подозревая, что, чтобы эти приборы работали, какие-то ученые составляли интегральные схемы, проводили исследования. И в каждом вашем сотовом телефоне находится интегральная схема.

Сообщение домашнего задания:

Базовый уровень: составить карточки с заданиями на вычисление определенного интеграла и его применение. Решить эти задания в тетради.

Творческое задание: исследовательским путем, вывести формулу вычисления объема шара.

Скачано с www.znanio.ru