Признаки равенства_прямоугольных_треугольников_Теор. материал

Определение. Прямоугольный треугольник – треугольник, один из углов которого прямой (равен ).

Прямоугольный треугольник – частный случай обычного треугольника. Поэтому все свойства обычных треугольников для прямоугольных сохраняются. Но есть и некоторые частные свойства, обусловленные наличием прямого угла.

Общепринятые обозначения (рис.1):

 – прямой угол;

 – гипотенуза;

 – катеты;

.

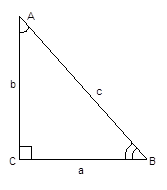
Признаки равенства прямоугольных треугольников:

1-й признак (по 2 сторонам и углу между ними): если у треугольников равны две стороны и угол между ними, то такие треугольники равны между собой.

2-й признак (по стороне и двум прилежащим углам): если у треугольников равны сторона и два угла, прилежащие к данной стороне, то такие треугольники равны между собой.Примечание: пользуясь тем, что сумма углов треугольника постоянна и равна , легко доказать, что условие «прилежания» углов не является необходимым, то есть признак будет верен и в такой формулировке: «… равны сторона и два угла, то …».

 3-й признак (по 3 сторонам): если у треугольников равны все три стороны, то такие треугольники равны между собой.

Естественно, все эти признаки остаются верными и для прямоугольных треугольников. Однако у прямоугольных треугольников есть одна существенная особенность – у них всегда есть пара равных прямых углов. Поэтому данные признаки для них упрощаются. Итак, сформулируем признаки равенства прямоугольных треугольников:

1-й признак (по двум катетам): если у прямоугольных треугольников катеты попарно равны, то такие треугольники равны между собой (Рис. 2).

Дано:

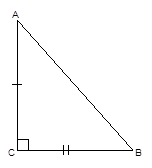
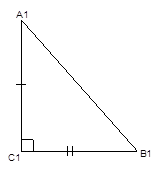
Рис. 2. Иллюстрация первого признака равенства прямоугольных треугольников

Доказать: 

Доказательство:  в прямоугольных треугольниках: . Значит, мы можем воспользоваться первым признаком равенства треугольников (по 2 сторонам и углу между ними) и получить: .

2-й признак (по катету и углу): если катет и острый угол одного прямоугольного  треугольника равны катету и острому углу другого прямоугольного треугольника, то такие треугольники равны между собой (Рис. 3).

Дано:

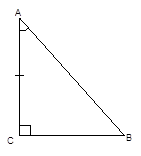
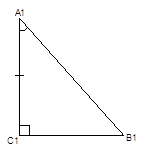
Рис. 3. Иллюстрация второго признака равенства прямоугольных треугольников

Доказать: 

Доказательство: сразу отметим, что тот факт, что равны углы, прилежащие к равным катетам, не является принципиальным. Действительно, сумма острых углов прямоугольного треугольника (по свойству 1) равна . Значит, если равна одна пара из этих углов, то равна и другая (так как их суммы одинаковы).

Доказательство же данного признака сводится к использованию второго признака равенства треугольников (по 2 углам и стороне). Действительно, по условию равны катеты и пара прилежащих к ним углов. Но вторая пара прилежащих к ним углов состоит из углов . Значит, мы можем воспользоваться вторым признаком равенства треугольников и получить: .

3-й признак (по гипотенузе и углу): если гипотенуза и острый угол одного прямоугольного  треугольника равны гипотенузе и острому углу другого прямоугольного треугольника, то такие треугольники равны между собой (Рис. 4).

Дано:

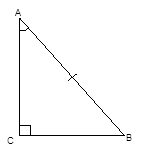
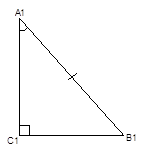
Рис. 4. Иллюстрация третьего признака равенства прямоугольных треугольников

Доказать: 

Доказательство: для доказательства этого признака можно сразу воспользоваться вторым признаком равенства треугольников – по стороне и двум углам (точнее, следствием, в котором указано, что углы не обязательно должны быть прилежащими к стороне). Действительно, по условию: , , а из свойств прямоугольных треугольников следует, что . Значит, мы можем воспользоваться вторым признаком равенства треугольников, и получить: .

4-й признак (по гипотенузе и катету): если гипотенуза и катет одного прямоугольного  треугольника равны соответственно гипотенузе и катету другого прямоугольного треугольника, то такие треугольники равны между собой (Рис. 5).

Дано:

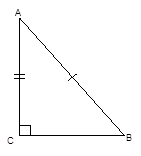
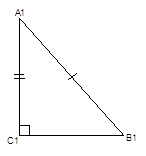
Рис. 5. Иллюстрация четвёртого признака равенства прямоугольных треугольников

Доказать: 

Доказательство: для доказательства этого признака воспользуемся признаком равенства треугольников, который мы сформулировали и доказали на прошлом уроке, а именно: если у треугольников равны две стороны и больший угол, то такие треугольники являются равными. Действительно, по условию у нас есть две равных стороны. Кроме того, по свойству прямоугольных треугольников: . Осталось доказать, что прямой угол является наибольшим в треугольнике. Предположим, что это не так, значит, должен быть ещё хотя бы один угол, который больше . Но тогда сумма углов треугольника уже будет больше . Но это невозможно, значит, такого угла в треугольнике быть не может. Значит, прямой угол является наибольшим в прямоугольным треугольнике. А значит, можно воспользоваться сформулированным выше признаком, и получить: .

Важно не путать признак со свойством – то есть, если треугольник прямоугольный, то у него есть такие свойства… Часто признаки и свойства являются взаимно обратными, но далеко не всегда. Например, свойство равностороннего треугольника: в равностороннем треугольнике есть угол . Но это не будет признаком равностороннего треугольника, так как не любой треугольник, у которого есть угол , является равносторонним.

Можно привести и более жизненный пример: свойство слова «хлеб» – в слове «хлеб» 4 буквы. Но наличие 4 букв не является признаком слова «хлеб», так как существует множество слов из 4 букв.

Признак прямоугольного треугольника (медиана равна половине стороны, к которой проведена)

Признак прямоугольного треугольника:

Если в треугольнике медиана равна половине стороны, к которой она проведена, то данный треугольник является прямоугольным, причём медиана проведена из вершины прямого угла.

Примечание: медиана – линия, соединяющая вершину треугольника с серединой противоположной стороны (Рис. 7).

Дано:

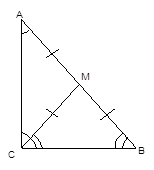
Рис. 7.

Доказать: 

Доказательство: поскольку , то  – равнобедренные. Значит, углы при основаниях каждого из этих треугольников равны. То есть, ,  .  Тогда сумма углов треугольника  равна  Значит, . Но: .

Скачано с www.znanio.ru