
План-конспект урока математики в 6 классе на тему: «ПРОПОРЦИИ».
Учитель математики: Хоружая Н. А.
Дидактическая цель. Ввести понятия пропорции и ее членов, сформулировать основное свойство пропорции.
Развивающая цель. Развить воображение, математическую интуицию, память, мышление; формировать правильность математической речи.
Воспитательная цель. Активизировать познавательную и творческую активность учащихся.
Оборудование: интерактивная доска,демонстративные карточки, таблицы, схемы.
Учебник: Математика: Учебник 6 кл. для общеобразовательных учреждений/ Н.Я. Виленкин, В. И, Жохов, А. С. Чесноков, С. И. Шварцбург.-22-е изд., испр.- М.: Мнемозина, 2008.
Тип урока: урок сообщения новых знаний.
ХОД УРОКА.
I. Организационный момент (2 мин.)
Проверить готовность учащихся класса к уроку. Отметить в журнале отсутствующих.
II.Устные упражнения по карточкам(8 мин)
1. Выразите в процентах числа:
|
0,2 |
|
0,15 |
|
1/2 |
|
3/5 |
|
3/4 |
|
1/20 |
|
20% |
15% |
50% |
60% |
75% |
5% |
Оборотная сторона карточки.
2. Сколько процентов составляет:
|
4 от 5 |
|
12 от 8 |
|
160 от 50 |
|
72 от 24 |
|
39 от 195 |
|
1/20 от 1/12 |
|
80% |
150% |
200% |
300% |
20% |
200% |
3. Найдите отношение:
|
6 к 20 |
|
8 к 40 |
|
|
|
|
|
|
|
|
|
|
|
|
Фронтальная работа. Числа изображены на карточках, которые демонстрируются учащимся поочередно. На обратных сторонах карточек записаны ответы (изображены частично пунктиром)
Сопутствующие вопросы:
1. Что называется отношением двух чисел?
2. Что показывает отношение двух чисел?
3. Какую часть первое число составляет от второго?
4. Сколько процентов одно число составляет от другого?
III. Изучение нового материала (15 мин).
1. Подготовительная работа.
-Придумайте отношения, равное 5.
-Если наши отношения равны 5, я могу записать из них равенства:
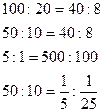
-Как по-другому можно записать равенство? (Записать частное в виде дроби.)
![]()
Определение. Равенство двух отношений называют пропорцией.
2.
Работа над новой темой.![]()
Общий вид пропорции:
a
: b=c : d ![]() или
или ![]()
Чтение записи a : b=c : d следующее:
«Отношение
a к b
равно отношению c к d»; Чтение записи ![]() :
«a так
относится к b, как c относится
к d».
:
«a так
относится к b, как c относится
к d».
Числа a и d называются крайними членами пропорции, а числа b и c – средними членами, a≠0, b≠0, c≠0, d≠0.
- Назовите крайние и средние члены пропорций.
средние
a : b = c : d
крайние
Задание 1. Установить является ли пропорцией равенство:
По каждой карточке задаются дополнительные вопросы; проверяются глубина знаний учащихся по теме: «Отношения» перед изучением нового материала.
Вопросы к учащимся.
Формулируется определение понятия пропорции записывается учащимися в тетрадь.
Используется схема, изображенная на плакате.
Задание записано на доске, Выполняется учениками устно
а) ![]() [ пропорция, так как 0,3=0,3];
[ пропорция, так как 0,3=0,3];
б)![]() [равенство не является пропорцией,
так как
[равенство не является пропорцией,
так как ![]() ].
].
Задание 2. В пропорции 2,4:0,6=8:2 найдем произведение её крайних и произведение её средних членов:
2,4·2=4,8 и 0,6·8=4,8.
Получим, что 2,4·2=0,6·8.
Задание 3. Найдите произведение крайних членов пропорции и произведение средних членов:
а)
![]() [6·9=3·18; 72=72];
[6·9=3·18; 72=72];
б)
![]()
-Что интересного заметили?
-Какой вывод можно сделать?
Вывод: Произведение крайних членов равно произведению средних членов.
Итак,мы вывели основное свойство пропорции.
В верной пропорции произведение крайних членов равно произведению средних.
-Верно ли обратное утверждение? Сформулируйте его.
Приведите свой пример.[Если произведение крайних членов равно произведению средних членов пропорции, то пропорция верна.]
Запишем основное свойство пропорции:
![]() ; a · d= b · c.
; a · d= b · c.
![]() или
a : b = c : d; a · d= b · c.
или
a : b = c : d; a · d= b · c.
![]()
И
обратно: если a · d= b
· c, то ![]() .
.
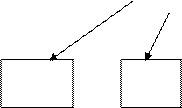
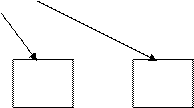
Далее создается проблемная ситуация: Можно ли из данной пропорции составить новые пропорции? Сколько?
На размышление учащимся дается две минуты, затем верное решение демонстрируется на доске с помощью следующей таблицы. (Таблица не убирается с доски до конца урока.)
Вывод делают сами ученики.
Вопросы к учащимся.
Запись в тетрадях учащихся.
![]()


![]() a : b = c : d
a : b = c : d

a · d= b · c
![]()
![]()
![]()
![]()
Задание 4. Используя верное равенство: 5·1,2=2·3, составьте четыре верные пропорции.
Решение. Из верного равенства 5·1,2=2·3 получаем четыре пропорции:
![]() - верная пропорция, так как
5·1,2=2·3, 6=6.
- верная пропорция, так как
5·1,2=2·3, 6=6.
![]() - верная пропорция;
- верная пропорция;
![]() - верная пропорция;
- верная пропорция;
![]() - верная пропорция.
- верная пропорция.
Используя основное свойство пропорции, можно найти ее неизвестный член, если все остальные члены известны.
Пример 1. Найдите в пропорции n:0,6=7:2,1 неизвестный крайний член n.
Решение. n:0,6=7:2,1;
n·2,1=0,6·7;
n=![]() ; n=
; n=![]() ; n=2.
; n=2.
Ответ: n=2.
Пример
2. Решим уравнение: ![]()
1 способ: 2 способ:
0,2·0,105=х·0,7.
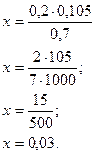
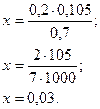
Ответ: х=0,03. Ответ: х=0,03.
У доски выполняет сильный ученик
Учащиеся записывают в тетрадях.
ВНИМАНИЕ!
Применение основного свойства пропорции при решении уравнений. Учащиеся записывают в тетрадях.
IV. Закрепление изученного материала.(15 мин)
№762(в, д - устно, а, е -письменно).
Решение.
в) неверная пропорция; д) верная пропорция;
а)
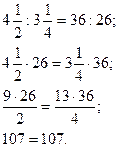 е)
е) 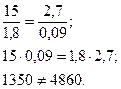
![]() - верная.
- верная. ![]() -
неверная.
-
неверная.
№763(в,г,д,з). Решить уравнение.
Ответы. в) ![]() ; г)
; г) ![]() ;
д) х=1,23; з) х=3.
;
д) х=1,23; з) х=3.
V. Домашнее задание (2 мин).
§4, п. 21, №№776, 777(а, в), 781(а).
VI. Подведение итогов урока ( 3 мин).
1. Что такое пропорция?
2. Сформулируйте основное свойство пропорции.
3. Сколько можно составить новых пропорций из данной?
Сообщаются оценки учащимся.
![]()
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.