РАБОЧАЯ ТЕТРАДЬ Интегральное исчисление (практическая подготовка)

ТАМБОВСКОЕ ОБЛАСТНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ПРОФЕССИОНАЛЬНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

«МНОГООТРАСЛЕВОЙ КОЛЛЕДЖ»

 

 

 

 

 

 

РАБОЧАЯ ТЕТРАДЬ

 

Интегральное исчисление

(практическая подготовка)

 

УЧЕБНО ПОСОБИЕ

по организации самостоятельной работы студентов

 

ЕН.01. «Математика»  для специальности 22.02.06 «Сварочное производство»

 

 

 

 

 

 

 

 

Автор(ы):                                        Трякин С.А., преподаватель 1 категории

ТОГБПОУ «Многоотраслевой колледж»;

Дорошенко И.В., Почётный работник воспитания и просвещения Российской Федерации, к. т. н, доцент, преподаватель ТОГБПОУ «Многоотраслевой колледж»

 

 

 

 

 

 

 

Моршанск, 2022г

 

Трякин С.А. Интегральное исчисление. ЕН.01. Математика. Учебное пособие по организации самостоятельной работы студентов/ Сост. С.А. Трякин, И.В. Дорошенко - Моршанск, 2022. - 22с.

Рабочая тетрадь по математике для студентов 2 курса (СПО) составлена в соответствии с действующей рабочей программой и учебниками по математике и может быть использована для самостоятельной работы студентов, а также для подготовки к промежуточной аттестации по математике.

Рабочая тетрадь представляет собой готовый дидактический материал для проведения практической подготовки (практических занятий) по ЕН.01 Математика.

Пособие адресовано преподавателям и студентам специальности 22.02.06 «Сварочное производство».

 

 

 

 

 

Рецензент(ы):                         Плохова О.В., зав. отделением

«Экономика и информационные технологии»

ТОГБПОУ «Многоотраслевой колледж»

Добычина Н.В., учитель математики высшей категории СОШ №3 г.Моршанск

СОДЕРЖАНИЕ

Пояснительная записка                                                                                 4

Основная часть                                                                                               6

1. Неопределенный интеграл                                                                        6

1. 1 Основные понятия                                                                              6

1. 2 Методы интегрирования                                                                     8

1. 3 Задания для самостоятельной работы                                                 10

1.4 Прикладное приложение неопределенного интеграла                        11

2. Определенный интеграл                                                                             12

2.1 Основные понятия                                                                               12

2.2 Задания для самостоятельной работы                                                 13

2.3 Геометрическое приложение определенного интеграла                     15

2.4 Практическая подготовка                                                                    16

Информационные источники                                                                        23

 

 

 

 

 

 

ПОЯСНИТЕЛЬНАЯ ЗАПИСКА

Рабочая тетрадь предназначена для организации самостоятельной работы по математике студентов второго курса, обучающихся по специальности 22.02.06 «Сварочное производство». Это учебное пособие, имеющее особый дидактический аппарат, способствующий самостоятельной работе студента по освоению учебной дисциплины в аудитории и дома, может быть использована студентами в самостоятельном освоении теоретического материала и формировании практических умений и навыков, при подготовке к промежуточной аттестации.

Материал тетради расположен в соответствии с логикой изложения темы в учебной программе и дисциплине ЕН.01. «Математика». При решении многочисленных задач проведения  технологического процесса изготовления сварных конструкций обычно реальное явление заменяется математической моделью. Модель является упрощенным представлением реальности. Главной задачей моделирования является максимальное приближение к реальности при достаточной простоте модели. В ряде случаев удается найти аналитическое решение профессиональной задачи.

В данном учебном пособии описан подход, позволяющий существенно ускорить процесс решения задач практической подготовки.

Рабочая тетрадь поможет преподавателю и студенту в организации самостоятельной работы как на уроке (с отдельными студентами, группой студентов или всей группой), так и дома.

Для студентов специальности 22.02.06 «Сварочное производство» вопрос применения интегрального исчисления для выполнения расчётов при освоении общеобразовательных дисциплин и профессиональных модулей, выполнении курсового и дипломного проектирования решает задачи:

- рационализации учебного процесса при совместном использовании лекционной части и рабочей тетради;

- новые возможности использования математической модели при решении инженерных задач;

- самостоятельного применения интегрального исчисления в вопросах технологии производства сварных конструкций, появляется резерв времени;

- возрастает информированность результатов расчетов с учетом графического изображения;

- результаты расчетов при использовании интегрального исчисления приемлемы в инженерных расчетах практической подготовки студентов с учетом будущей профессиональной деятельности.

Результаты освоения темы являются частью общих компетенций соответствующих видам профессиональной деятельности:

ОК 1. Понимать сущность и социальную значимость своей будущей профессии, проявлять к ней устойчивый интерес.

ОК 3. Решать проблемы, оценивать риски и принимать решения в нестандартных ситуациях

ОК 5. Использовать информационно-коммуникационные технологии для совершенствования профессиональной деятельности.

ОК 8. Самостоятельно определять задачи профессионального и личностного развития, заниматься самообразованием, осознанно планировать повышение квалификации.

ОК 9. Быть готовым к смене технологий в профессиональной деятельности.

Актуальность данного пособия вызвана необходимостью подготовки специалистов, имеющих навыки работы с математической моделью производственной ситуации.

Цели:

Образовательная: Активизировать деятельность студентов, повысить престиж знаний, творческих возможностей студентов, их самоутверждение и реализацию.

Развивающая: развить организационные способности студентов, самостоятельность, создать развивающее пространство для творческой активности студентов.

Воспитательная: воспитать любовь к выбранной профессии, значимости этой профессии, развить кругозор, воспитать умение оценивать себя.

Структура практических занятий состоит из заданий: "Закончите предложение и заполните пропуски", "Ответьте на вопросы" и "Решите самостоятельно". Применение различных видов заданий позволяет проверить как теоретические, так и практические знания студентов. Задания ориентированы на учебник Богомолова Н.В.

Критерии оценки выполнения заданий:

Отметка «5» ставится, если:

- задание выполнено полностью;

- в логических рассуждениях и обосновании решения нет пробелов и ошибок;

- в решении нет математических ошибок (возможна одна неточность, описка, не являющаяся следствием незнания или непонимания учебного материала).

Отметка «4» ставится, если:

- задание выполнено полностью, но обоснования шагов решения недостаточны (если умение обосновывать рассуждения не являлось специальным объектом проверки);

- допущена одна ошибка или два-три недочета в рисунке или графике  (если этот вид работы не являлись специальным объектом проверки).

Отметка «3» ставится, если:

- допущены более одной ошибки или более двух-трех недочетов, но студент владеет обязательными умениями при выполнении задания.

Отметка «2» ставится, если:

- допущены существенные ошибки, показавшие, что студент не владеет обязательными умениями по данной теме в полной мере.

ОСНОВНАЯ ЧАСТЬ

Задачей интегрального исчисления является нахождение функции по заданной её производной.

1. Неопределенный интеграл

1.1 Основные понятия

Определение 1. Первообразной F(x) функции у=f(x) на промежутке (a1;a2) называется такая функция, что будет выполняться равенство ___________________, для любого x из промежутка (a1;a2).

Например, для функции y=sin(x) на множестве действительных чисел первообразной будет функция F(x)=-cos(x), так как _____________________.

Вспомним, что производная любой константы равна нулю, то есть, если C-некоторая константа, то С'=0.

Имеем: если F(x) первообразная для функции y=f(x), то и функция (F’(x)+C) также будет являться первообразной для функции y=f(x). Действительно (F(x)+C)’=_________________________=F’(x).

Задание. Докажите, что функции , ,  являются первообразными для одной и той же функции. Сделайте вывод.

____________________________________________________________________

____________________________________________________________________

____________________________________________________________________

____________________________________________________________________

____________________________________________________________________

__________________________________________________________________

Теорема1. Если функция y=f(x) имеет первообразную, то она имеет _____________________ первообразных, отличающихся свободным членом.

Говорят, что все первообразные одинаковые с точностью до свободного члена.

Задание. Используя таблицу производных, найдите три первообразных для функции

____________________________________________________________________

__________________________________________________________________

__________________________________________________________________

__________________________________________________________________

Определение 2. Множество всех первообразных функции y=f(x) называется неопределенным интегралом данной функции и обозначается .

где:

               ______________________________

f(x) -             ______________________________

f(x)dx -         ______________________________

 

Свойства неопределенного интеграла:

I. Постоянный множитель можно выносить за знак интеграла

ò kf (x)dx = _________________

 

II. Интеграл суммы равен сумме интегралов слагаемых

________________________ =òf (x)dx ± ò g(x)dx

 

Пример. Найти . Так как (, то функция F(x)= является одной из первообразных для функции , следовательно

 , где С – некоторая константа (С=const).

Заполните таблицу неопределенных интегралов основных элементарных функций.

 

1.2 Методы интегрирования

Непосредственное интегрирование

Интегрирование осуществляется на основе таблицы интегралов элементарных функций и свойств неопределенного интеграла.

Пример. Найти неопределенный интеграл с помощью таблицы неопределенных интегралов.

1) .

Воспользуемся формулой (1), где α=3. Получим:

2) .

Воспользуемся формулой (1) и свойством (II). Получим:

 

 

Интегрирование с помощью замены переменной (метод подстановки)

Интегрирование осуществляется с помощью замены некоторого подынтегрального выражения на новую переменную и замены оставшейся части на новый дифференциал.

Пример. Найти неопределенный интеграл методом замены переменной.

1)

Сделаем замену 5x-3=t, будем иметь:

 

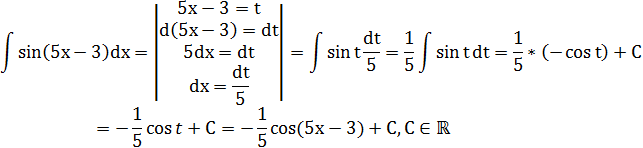
2)

 

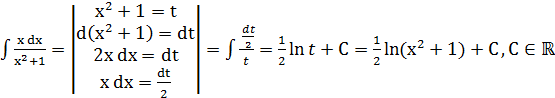
Интегрирование по частям

Чаще всего интегрирование по частям применяется в случае наличия показательных, логарифмических, прямых и обратных тригонометрических формул и их сочетаний в подынтегральном выражении.

Основная формула, необходимая для использования этого метода, выглядит так:

Пример. Найти неопределенный интеграл методом интегрирования по частям.

1)

 

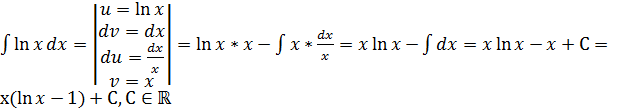
2)

 

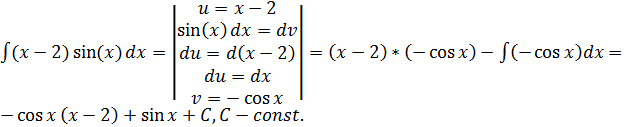
1.3 Задания для самостоятельной работы

Вычислить неопределенные интегралы

1)  _________________________________________________________________________________________________________________

 

2)  _______________________________________________ _____________________________________________________________

 

3)  _________________________________________ _____________________________________________________________ _____________________________________________________________

 

4)  _______________________________________________ _____________________________________________________________ _____________________________________________________________

 

5)  _______________________________________________ __________________________________________________________________________________________________________________________

 

6)  ____________________________________________________ __________________________________________________________________________________________________________________________

 

7)  _______________________________________________________________________________________________________________________________________________________________________________

 

8)  ______________________________________________________________________________________________________________________________________________________________________________

 

9)  ______________________________________________________________________________________________________________________________________________________________________________

 

10)            _____________________________________________________________________________________________________________________________________________________________________

 

11)            ________________________________________ __________________________________________________________________________________________________________________________

 

12)            _______________________________________ __________________________________________________________________________________________________________________________

 

13)            ______________________________________ __________________________________________________________________________________________________________________________

 

14)            __________________________________________ __________________________________________________________________________________________________________________________

 

1.4 Прикладное приложение неопределенного интеграла

Скорость сварки Vсв (м/ч) можно определить по формуле

, где n – число потраченных электродов (шт), t - основное время горения дуги(ч).

Тогда закон длины шва (мм) от времени примет вид:

Пример. Найти закон длины шва (мм), если за 1,5 часа сварной шов имеет длину 1,6м и потратили 20 электродов.

Откуда имеем, что С ≈626,88.

Закон длины шва при таких начальных условиях примет вид

 

Задания для самостоятельной работы

1)              Пусть закон скорости сварки имеет вид , где n – число потраченных электродов (шт), t - основное время горения дуги(ч). Найдите общий закон длины сварного шва в зависимости от времени сварки. Найдите закон длины сварного шва при условии, что за 2ч 20 минут было израсходовано 25 электродов, а длина шва составила 2,1 метра.

________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

 

2 Определенный интеграл

2.1. Основные понятия

Определение. Определенным интегралом функции y=f(x) на отрезке [a;b] называется предел (если он существует) ее интегральной суммы

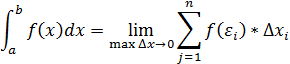
Для вычисления определенного интеграла используется формула Ньютона-Лейбница

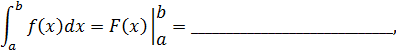
где F(x) одна из первообразных функции y=f(x).

 

Примеры.

Найти значение определенных интегралов, приведенных ниже:

1)                    Непосредственное интегрирование по формулам

 

 

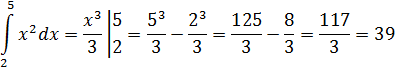
2)                    Метод замены переменной (подстановки)

a)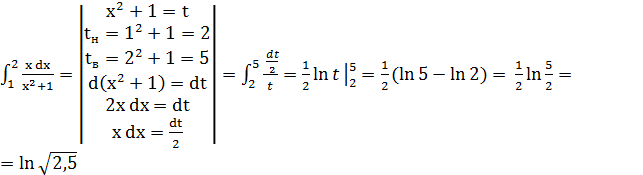

 

б)

=

 

 

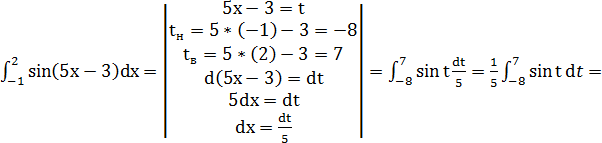
3)    Метод интегрирования «по частям»

а)

 .

 

 

 

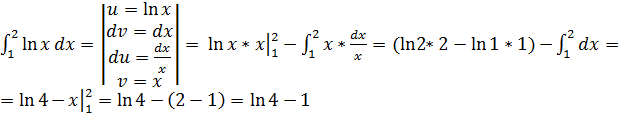б)

 

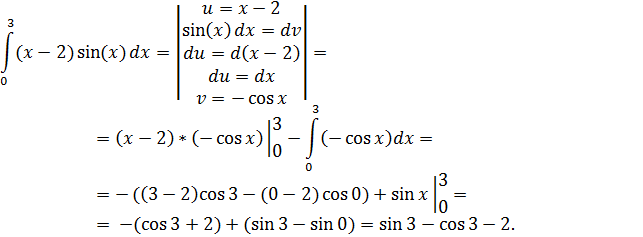
2.2 Задания для самостоятельной работы

Вычислить определенные интегралы

1)  _________________________________________________________________________________________________________________________________________________________________________

 

2)  _____________________________________________ _______________________________________________________________________________________________________________________

 

3)  _________________________________________ _____________________________________________________________ _____________________________________________________________

 

4)  ____________________________________________ _____________________________________________________________ _____________________________________________________________

 

5)  _____________________________________________ __________________________________________________________________________________________________________________________

 

6)  ___________________________________________________ __________________________________________________________________________________________________________________________

 

7)  ______________________________________________________________________________________________________________________________________________________________________________

 

8)  _____________________________________________________________________________________________________________________________________________________________________________

 

9)  ____________________________________________________________________________________________________________________________________________________________________________

 

10)            _____________________________________________________________________________________________________________________________________________________________________

 

11)            _______________________________________ __________________________________________________________________________________________________________________________

 

12)            ______________________________________ __________________________________________________________________________________________________________________________

 

13)            _____________________________________ __________________________________________________________________________________________________________________________

 

14)            _________________________________________ __________________________________________________________________________________________________________________________

 

2.3 Геометрическое приложение определенного интеграла

1. Площадь криволинейной трапеции (см. рисунок 1), ограниченной линиями _______________________________________________________________,

равна .

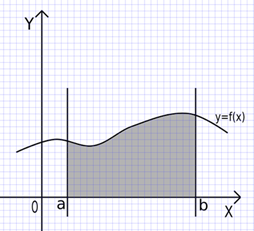
Рисунок 1

Пример. Найти площадь криволинейной трапеции, ограниченной линиями: x=1, x=3, , осью OX.

 

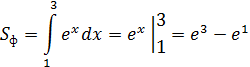
2.4 Практическая подготовка

Практическая подготовка — выполнение студентами  заданий, связанных с будущей профессиональной деятельностью и направленных на формирование, закрепление, развитие практических навыков и компетенции по МДК 01 Технология сварочных работ.

Вычислить площадь боковой поверхности опоры цилиндрической емкости, имеющий вид, представленный на рисунке 2.

Рисунок 2

 

Разместим оси координат следующим образом: ось ОX направим по нижней части опоры, ось OY по вертикальной осевой. За единичный отрезок примем 1 мм. При таком расположении получим рисунок 3

Рисунок 3

Имеем. Окружность с центром в точке (0;1000) радиусом 850.

Уравнение данной окружности имеет вид:

При переходе к функции будем иметь:

Имеем дело с нижней частью окружности, тогда функция примет вид:

Используя формулу для вычисления площади криволинейной трапеции получим:

 

 

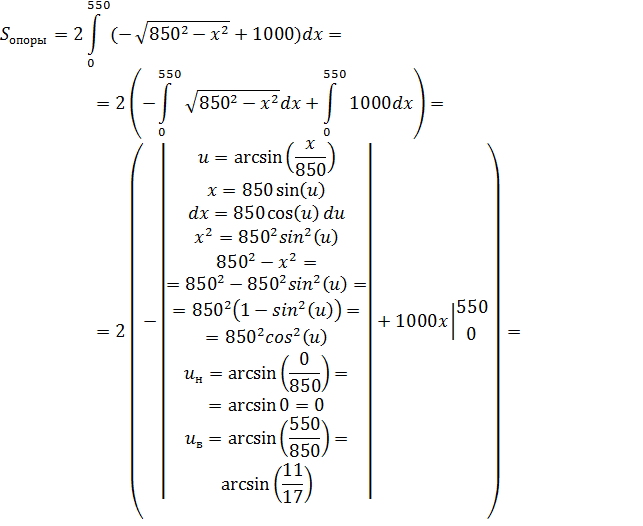
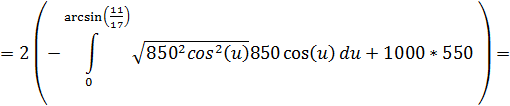
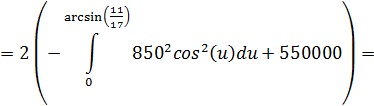
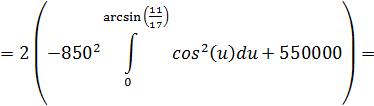
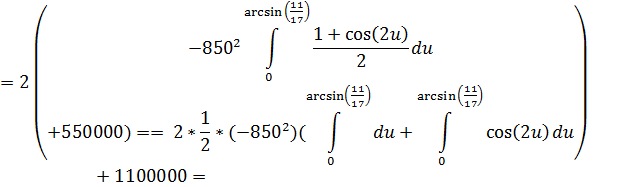
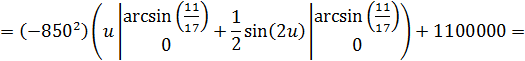
Применяя вычислительную технику, получим следующее (с точностью до пяти знаков после запятой)

-722500(0.70372+0,5sin(2*0.70372))+110000=

=-722500*(0.70372+0,5*sin(1,40744))+1100000≈

≈-722500*(0.70372+0,5*0,98669)+1100000=235 121,62129 мм²

Видим, что расчет полностью (до десятых долей миллиметра квадратного) совпадает с расчетами САПР «Компас 3D» (см. рисунок 4)

 

Рисунок 4

Задания для самостоятельной работы:

Вычислить площадь боковой поверхности детали, изображенной на чертеже. Результат проверить с помощью чертежа в САПР «Компас 3D».

1) Серьга (рисунок 5)

Рисунок 5

________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

2) Отражатель (рисунок 6)

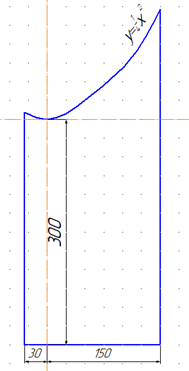
Рисунок 6

 

________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

ИНФОРМАЦИОННЫЕ ИСТОЧНИКИ

1. Богомолов, Н. В.  Математика : учебник для среднего профессионального образования / Н. В. Богомолов, П. И. Самойленко. — 5-е изд., перераб. и доп. — Москва : Издательство Юрайт, 2018. — 401 с. — (Профессиональное образование).

2. Овчинников, В.В. Справочник техника-сварщика / В.В. Овчинников. - М.: ИД ФОРУМ: НИЦ ИНФРА-М, 2021. - 304 с.

3. Виртуальная библиотека для сварщика: –URL: //http://www.svarkainfo.ru/rus/lib/books/