РАЙОННАЯ НАУЧНО-ПРАКТИЧЕСКАЯ КОНФЕРЕНЦИЯ ШКОЛЬНИКОВ «К ВЕРШИНАМ ЗНАНИЙ»

РАЙОННАЯ НАУЧНО-ПРАКТИЧЕСКАЯ КОНФЕРЕНЦИЯ ШКОЛЬНИКОВ

 «К ВЕРШИНАМ ЗНАНИЙ»

Секция «                           »

Тема: «Математическая география или географическая математика»

 

Выполнил :Митичкин ИванАнтонович,

МБОУ СОШ№148Купинского района 8  класс.

Руководители: Манжаева Ирирна Николаеана,

 учитель (географии)

 высшей квалификационной категории

контактный телефон:8-913-395-43-18

Савостьянова Валентина Витальевна

учитель (математики)

 высшей квалификационной категории

контактный телефон:8-913-454-59-44                                                    

      

 

 

 

 

2022 год.

 

 

Содержание

Введение Глава 1. Теоретическая часть. Взаимосвязь математики и  географии 1.1. Математика как наука 1.2.  География как наука 2. Взаимосвязь географии и математики 2.1 Масштаб 2.2 Географическая карта 2.3 Климат и погода 2.4 Плотность населения Купинского района Заключение

 

 

 

 

 

 

 

 

 

 

 

 

 

Введение.

 

Математика и география – это две науки тесно связанные между собой. Математика позволяет определить обычные явления в природе, обществе, даже в нашем городе  и в стране, которые основываются на приблизительных описаниях, на язык точных формул, которые можно получить не приблизительно, а точно. География складывается из всего окружающего: леса, океаны, пустыни, почва, общество, экономические отношения, животные и растения, климат и погода, круговорот веществ в природе и многое другое.

Каждая из цивилизаций, начиная с древнего мира, вырабатывала свои собственные, неповторимые пути познания мира, уникальные понятия, с помощью которых обдумывалось и излагалось полученное знание. Определить количество жителей, проживающих на определённой территории, рассчитать рельеф местности, измерить территорию, чтобы создать замечательное изобретение человечества- карту. «Рассчитать» - это главное слово, из всего выше сказанного.

Только с использованием «чисел», главного и основного орудия «царицы всех наук» - математики, можно познать одну из самых трудно-поддающихся изучению, науку географию.

        Меня заинтересовала данная тема, и я решил проследить и показать в своей работе, как связаны между собой две науки: математика и география. Поэтому выражение великого Канта: «Математика- это наука, брошенная человечеством на исследование мира во всех его возможных вариантах» и  выражение знаменитого греческого географа Страбона «Для такого предмета как география более всего необходимы геометрия и астрономия“ четко определяет, почему я выбрал тему. Я  люблю математику, и хочу познать мир, с помощью точного и понятного мне школьного предмета.

Актуальность  проекта : В пятом классе у нас появился новый предмет – география. С первого урока для нас было  удивлением, что география очень древняя наука, которая зародилась в античное время, и  связана с многими науками, особенно с математикой. В дальнейшем пришло убеждение  в том что, когда определяли  азимут и расстояние по плану местности, географические координаты по карте, мне стало интересно, а связана ли математика с другими темами по географии? Это я и  решил проверить на практике и попытался проследить связь математики и географии.                    

Новизна исследования состоит в том, что в работе впервые приведены примеры взаимосвязи математики и географии на основе изучения данных Купинского района.

 

Цель исследования: доказать взаимосвязь математики и географии.

Задачи исследования:

1) показать важность математики в географии и способы ее применения;

2) привести примеры использования математического метода в географии.

Гипотеза: математика и география очень тесно связаны между собой; без математики географии было бы очень трудно существовать.

Объект исследования: математика и география как самостоятельные науки.

Предмет исследования: математические методы в географии.

Методы исследования: информационный, социологический и аналитический.

Практическая значимость данного проекта носит просветительский характер и нацелена на повышение интереса и внимания учащихся к изучению таких школьных предметов как математика и география. Материал может быть использован на уроках и  при проведении внеклассной работы по данным предметам.

1. Теоретическая часть.

1.1. Математика, как наука

«Разве ты не заметил, что способный к математике изощрен во всех науках в природе?»

                                                                                                                                        (Платон)

Если перенести эту мысль на наши дни — это значит, что математика может быть полезна практически в любом деле: управлять компанией, программировать сайты и приложения, анализировать данные, конструировать здания или роботов, можно стать метеорологом или финансистом, преподавателем, политиком и т.д.

Математика развивает логическое мышление, способность рассуждать последовательно, обоснованно и находить решения самым разным задачкам — не только математическим, но и жизненным.

Слово «математика» произошло от  греческого mathema, что обозначает знание, умение, наука. Математика – это наука о количественных  отношениях  и пространственных формах окружающего нас мира . 

Математика – древнейшая наука в истории человечества. Представления человека о числе относятся к очень далекой эпохе древнего каменного века. Самой древней математической деятельностью был счет. Счет был необходим, чтобы следить за поголовьем скота и вести торговлю.

Некоторые первобытные племена подсчитывали количество предметов, сопоставляя им различные части тела, главным образом пальцы рук  и ног. Наскальный рисунок, сохранившийся до наших времен от каменного века,  изображает число 15 в виде выстроенных в ряд 15 палочек - пальцев.

Дальнейшее развитие математики происходило примерно  в  3000  до  н. э. благодаря вавилонянам и египтянам. В то время математика в основном была связана с ведением хозяйства. Математические знания использовались при обмене денег и расчетах за товары, для вычисления налогов и доли урожая, которую нужно было отдавать в пользу государства, храма или землевладельца. Многочисленные арифметические и геометрические задачи решались людьми при строительстве домов, храмов, каналов, хранилищ для зерна. Без применения математики невозможны были исследования движений Луны и планет. А это позволило людям предсказывать положения планет. Очень важной задачей математики был расчет календаря, поскольку календарь использовался для определения сроков сельскохозяйственных работ и религиозных праздников.

Греки в течение 1-2 столетий сумели овладеть математическим наследием своих предшественников, но они не остановились на достигнутом и продолжали развивать математическую науку дальше. Греки были, прежде всего, геометрами. Геометрия буквально означает «землемерие». Многим из нас известны имена древнегреческих ученых Фалес, Пифагор, Евклид, Платон, Аристотель, Архимед. С тех времен математика стала не просто наукой для ведения простых хозяйственных подсчетов, а она стала инструментом для выявления сущности явлений и процессов.

Свой вклад в развитие математики внесли индийцы и арабы. Немаловажно было то, что арабские математики переписывали труды греческих математиков, комментировали и совершенствовали их. Многие их работы послужили основой для последующего развития математики в Европе.

В средние века основой развития математической науки служило интенсивное развитие ремесел, производства товаров и торговля. Для развития математики большую роль сыграли переводы на латинский язык сочинений арабских математиков. Европейцы смогли познакомиться с трудами Архимеда, Евклида и других греческих математиков. Открывались первые университеты .

В XVI-XVII вв. математика развивалась в Италии, Франции, Германии, Голландии. Появляются новые математические теории, математические вычисления становятся все более сложными. В математике начинают видеть метод изучения природы.

Какие бы крупные изменения не происходили за тысячи лет с человеческой цивилизацией, все время на помощь людям приходила математика. Ведь все события, происходящие с человечеством, не могли обойти стороной науку. Менялось общество, менялась и наука.

Сейчас человечество решает много разных вопросов. Это и политика, и экономика, и экология и многое другое. Все это, заставляет человеческий интеллект искать пути решения для того, чтобы управлять сложными системами природы. Здесь на помощь людям приходит прогнозирование.

Математика дала возможность осуществить технологический прогресс человечества, она стала той самой необходимой частью этого прогресса. Возникновение и развитие мировой науки и компьютерной математики позволило и позволяет человечеству избежать ряда социальных, экономических и технических катастроф .

1.2. География, как наука

География – также как и математика является древнейшей наукой. Слово «география» произошло от греческого ge – «земля» и grapho – пишу. География (греч. - “землеописание”) - наука, изучающая поверхность Земли, облегающие и подстилающие её слои вещества, которые в совокупности образуют географическую оболочку. Истоки географии уходят вглубь веков гораздо дальше, чем, например, у физики, химии, биологии, геологии и многих других наук .

В течение многих веков география существовала как описательно-познавательная наука, географы открывали и описывали ранее неизвестные страны и земли. География столетиями накапливала факты и ее главная задача состояла в том, чтобы шаг за шагом создавать картину поверхности земного шара, т.е. нанести на карту и описать берега материков и островов, горы, реки, озера и т.д.

Не следует, конечно, думать, что географы в прошлом были только собирателями фактов, среди них были и выдающиеся мыслители. Уже в глубокой древности люди пытались объяснить разливы рек, приливы и отливы, происхождение ветров и течений и многие другие географические явления. Но общий уровень науки был таким, что ученые не могли экспериментально исследовать наблюдаемые явления, и им приходилось догадываться об их сущности и происхождении, полагаясь на свою интуицию или фантазию.

Только к концу прошлого века география смогла опереться на основные законы физики, химии и биологии, чтобы изучать и объяснять сложные явления и процессы, которые происходят в земной поверхности. Таким образом, география начала превращаться из описательной (“собирательной”) дисциплины в науку теоретическую.

Современная география – это целая “семья” наук, которые изучают природу, законы развития хозяйства, условия жизни населения. Одна из важнейших задач современной географии - изучение того, как существовать природе и человеку для правильного использования природных ресурсов и сохранения благоприятных условий для жизни человека на нашей планете.

Зачатки географических знаний появились еще у первобытных людей, ведь их жизнь зависела от того, как они умеют ориентироваться в пространстве и отыскивать естественные убежища, источники воды, места для охоты, камни для орудий и т.д. Первобытный человек отличался острой наблюдательностью и даже умением делать рисунки местности на шкурах, бересте, дереве - прообразы наших географических карт.

А первые географические письменные документы оставили нам земледельческие народы Древнего Востока: Египта, Двуречья, Северной Индии и Китая. Так, в Египте для определения сроков различных сельскохозяйственных работ стали проводиться регулярные астрономические наблюдения. Египтяне довольно точно определили продолжительность года и ввели солнечный календарь. Древним египтянам и вавилонянам были известны солнечные часы. Египетские и вавилонские жрецы, а также китайские астрономы установили закономерности повторения солнечных затмений и научились предсказывать их. Из Двуречья происходит деление года - на 12 месяцев, суток - на 24 часа, окружности - на 360 градусов; там же было введено понятие “лунная неделя”.

В Древней Греции около 500 г. до н.э. Аристотель впервые высказал идею о том, что Земля имеет форму шара. Он доказывал свою идею тем, что: у земной тени при лунных затмениях наблюдалась круглая форма, и вид звездного неба при передвижении с севера на юг изменялся.

Около 165 г. до н.э. греческий ученый Кратес изготовил первую модель земного шара - глобус.

Аристарх Самосский в III в. до н.э. впервые приблизительно определил расстояние от Земли до Солнца. Он первым начал учить, что Земля движется вокруг Солнца и вокруг своей оси.

В Древней Греции зародились основные направления географической науки. Нужды мореплавания и торговли (греки основали в то время ряд колоний на берегах Средиземного и Черного морей) вызвали необходимость в описаниях суши и морских берегов.

В Греции возникло новое географическое направление, которое получило впоследствии название математической географии. Одним из первых представителей этого направления был Эратосфен из Кирены (276-194 гг. до н.э.). Древнегреческий учёный Эратосфен изобрел систему координат, покрыв свою карту сеткой из перекрещивающихся горизонтальных и вертикальных линий. Он первым ввел понятие параллели и меридиана. Немного линий было на карте Эратосфена, и нанесены они были на разном расстоянии друг от друга, все это мало походило на градусную сеть. И, тем не менее, новая страница познания Земли была открыта. Эратосфен показал на своих картах новые пути, например, путь в Индию, которым гораздо позже воспользовался Колумб.

В по­сле­ду­ю­щее время также было со­зда­но много географических карт  по мере от­кры­тия новых тер­ри­то­рий. Ко­неч­но, эти карты были да­ле­ки от иде­а­ла, но все равно имели огром­ное зна­че­ние и яв­ля­лись по­ка­за­те­лем про­грес­са гео­гра­фи­че­ских зна­ний.

В пе­ри­од Ве­ли­ких гео­гра­фи­че­ских от­кры­тий в Гер­ма­нии был со­здан пер­вый гло­бус. При­ме­ча­тель­ным яв­ля­ет­ся тот факт, что на нем не были изоб­ра­же­ны тер­ри­то­рии Се­вер­ной и Южной Аме­ри­ки, так как ле­ген­дар­ное пу­те­ше­ствие Хри­сто­фо­ра Ко­лум­ба еще было в бу­ду­щем.

Вер­сия Ари­сто­те­ля о том, что Земля имеет форму шара, окон­ча­тель­но под­твер­ди­лась толь­ко в 1522 году, когда кру­го­свет­ная экс­пе­ди­ция Ма­гел­ла­на пе­ре­сек­ла Тихий океан.

Имена пер­во­от­кры­ва­те­лей, ис­сле­до­ва­те­лей со­хра­ни­лись на гео­гра­фи­че­ских кар­тах, их име­на­ми на­зва­ны раз­лич­ные гео­гра­фи­че­ские объ­ек­ты (на­при­мер, ост­ров Кука, море Лап­те­вых, Ма­гел­ла­нов про­лив и т.д.).

Сей­час от­кры­ты все ма­те­ри­ки, ост­ро­ва, моря, оке­а­ны, и Земля видна как на ла­до­ни из кос­мо­са. В на­сто­я­щее время про­ис­хо­дит более по­дроб­ное изу­че­ние по­верх­но­сти пла­не­ты, дна оке­а­на, внут­рен­них ча­стей Земли, изучение кли­ма­ти­че­ских яв­ле­ний с по­мо­щью со­вре­мен­ных при­бо­ров и зна­ний. При изу­че­нии Земли ак­тив­но при­ме­ня­ют­ся не толь­ко гео­гра­фи­че­ские ме­то­ды и зна­ния, но и до­сти­же­ния мно­гих дру­гих наук .

2.Исследовательская часть.

Взаимосвязь географии и математики

Необходимость применения математики в географии возникла потому, что со времен возникновения человеческой цивилизации увеличивалось количество человеческих открытий, осваивались новые земли, строились города, и поток географической информации все увеличивался. Он охватывал множество стран, городов, народов, все части и явления природы, население, культуру и многое другое, и становился огромным и необозримым. Тогда на помощь географам пришла математика.

Первые опыты применения математики в географии, как отмечают исследователи, относятся к временам древнегреческих ученых Фалеса Милетского и Эратосфена. Так называемая, математическая география в те древние времена занималась вычислением параметров Земли как планеты, расчетом ее форм и размеров. На карте, созданной Эратосфеном, мы можем видеть вертикальные и горизонтальные линии - это меридианы и параллели.

Параллели и меридианы – это воображаемые линии на поверхности Земли, они проходят через любую точку поверхности Земли. Любая точка на Земле – это пересечение параллели и меридиана и она имеет свои координаты. Немного линий было на карте Эратосфена, и нанесены они были на разном расстоянии друг от друга, мало походя на современную градусную сеть. И, тем не менее, новая страница познания Земли была открыта.

Эратосфен показал на своих картах новые пути, например, путь в Индию, которым гораздо позже воспользовался Колумб. Сегодня мы не представляем нашу жизнь без географических координат. Координаты задает капитан в навигационной системе корабля, летчик в самолете, водитель в своем автомобиле пользуется навигатором.

В средние века и во времена Великих географических открытий люди больше занимались землеописанием, связанным с открытием новых мест на планете Земля. И если в данный период и можно указать на ряд опытов применения математических методов в географии, то это скорее случайности, нежели закономерный процесс вхождения математики в географию.

Но уже, в начале XX в. появилась научная основа применения математики в географии. Появились ученые, которые серьезно работали в этой области. Чем они занимались? Они проводили статистические наблюдения, т.е. собирали сведения о каком-либо явлении, затем эти сведения обрабатывали при помощи математических формул. Таким образом, вырисовывалась картина закономерности многих явлений и процессов в географии.

Такую картину сейчас называют – «математическая модель». Это отображение географических явлений математическими формулами. Математические модели хорошо показывают, как с течением времени изменяются наблюдаемые географические явления. Модели позволяют «проигрывать» возможные ситуации развития какого-либо явления и получать самое лучшее решение, а также делать прогнозы. Такое математическое моделирование очень помогает при наблюдении за вулканами, землетрясениями, наводнениями и другими объектами. В настоящее время в географии используются достаточно сложные методы математического моделирования.

2.1Масштаб

Как же человек научился наносить географические объекты на карту, ведь их размеры так отличаются друг от друга, а язык карты должен быть точным? И здесь на помощь людям приходит математика. Мы видим это из научного определения карты, которое гласит: «Карта – это уменьшенное, обобщенное изображение поверхности, построенное по математическому закону на плоскости и показывающее посредством условных знаков размещение и свойства объектов».

Для изображения географических объектов на карте применяется масштаб. Масштаб был придуман ещё до нашей эры Евклидом, а полное определение “масштаба” звучит так: «Отношение длины отрезка на карте к длине соответствующего отрезка на местности называют масштабом». Масштаб (от немецкого - мера и Stab - палка) - это отношение длины отрезка на карте, плане, аэро- или космическом снимке к его действительной длине на местности. Масштаб — это дробь, у которой в числителе единица, а знаменатель — число, указывающее, во сколько раз расстояние на карте меньше, чем сама местность.

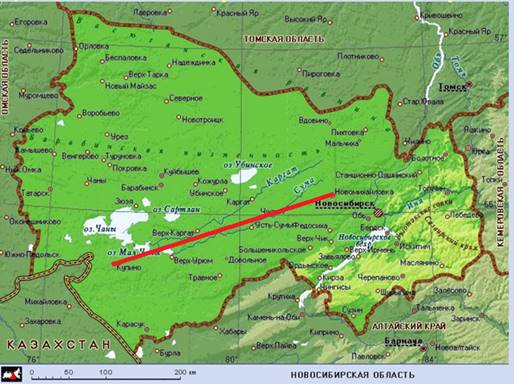
Определим кратчайшее расстояние между г. Купино и г. Новосибирск. Выбираем карту масштаб 1: 50, что означает, что в 1 см на карте равен 50 км на местности. Соединяем отрезком данные пункты и измеряем длину отрезка. Это расстояние равно 8 см. И 50 * 8=400 км. Так при помощи масштаба поместились на наши карты - все реки, горы, моря и океаны нашей планеты.

2.2 Географические координаты

Все путешественники должны быть вечно благодарны древнегреческому учёному Гиппарху, который около 100 лет до н.э. предложил нарисовать на географической карте параллели и меридианы и обозначить цифрами широту и долготу.

 

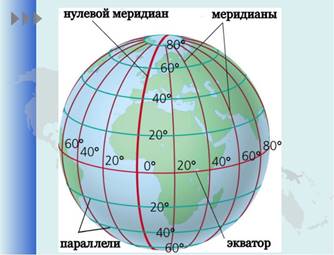
Долгое время лишь география («землеописание») пользовалась этим изобретением. И только в XIV в. французский математик Никола Оресм попытался приложить его к геометрии («землеизмерению»). Он нарисовал на плоскости сетку из прямых линий, пересекающихся под прямыми углами, и стал задавать местоположение точек широтой и долготой.

Первым, кто по достоинству оценил новшество, был великий француз Рене Декарт (1596-1650). Его имя носит теперь прямоугольная система координат, обозначающая место любой точки плоскости расстояниями от этой точки до «нулевой широты» – оси абсцисс и «нулевого меридиана» – оси ординат. По традиции, введенной Декартом, «широта» обозначается буквой Х, «долгота» – буквой Y.

 

.

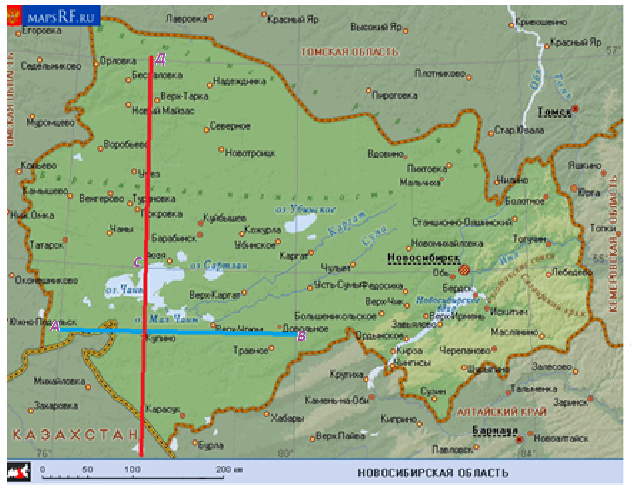
Определим географическое положение г. Купино по карте Новосибирской области. Проведем линии параллельные меридианам и параллелям через точку указывающую г. Купино. Наш город  находится между 76⁰ и 80⁰ меридианами   и 53⁰ и 55⁰параллелями. Делаем расчеты: а) между меридианами  АВ=8см, что соответствует 4⁰,следовательно, 1см-0,5⁰.Купино отдалено от 76⁰ меридиана(точки А) на 2,6см или 0,5⁰ *2,6=1,3⁰. Поэтому, 76⁰ +1,3⁰ =77,3⁰ северная широта г. Купино,

Б)  длина отрезка СД=7см,  а 55⁰ -53⁰ =2⁰,   т.е. 1см=⁰, Купино находится ниже 55⁰ параллели на 2,1см,следовательно,  ⁰ *2,1=0,6⁰. Поэтому 55⁰ -0,6⁰ =54,4⁰восточная долгота г. Купино.

2.3 Климат и погода

Температура, влажность, потоки энергии в атмосфере, скорость и направление ветра, осадки и их интенсивность постоянно изменяются от места к месту, от часа к часу.

Поток географической информации увеличивался – осваивались новые земли, строились города и тогда на помощь географам пришла математика. Географы проводили наблюдения за явлениями природы, собирали о них сведения, затем эти сведения обрабатывали при помощи математических формул. Таким образом, в географии появилась математическая статистика, которая показывала закономерности многих явлений и процессов в географии, например, прогноз погоды.

Расположение метеорологической станции в Купино (Новосибирская область, Россия):
широта 54.38 долгота 77.32 высота над уровнем моря 116 м.

 

годы	январь	февраль	март	апрель	май	июнь	июль	август	сентябрь	октябрь	ноябрь	декабрь	За год
2010	-26.7	-23.6	-9.0	4.2	10.3	17.9	17.5	18.2	11.2	4.4	-2.4	-19.4	0.2
2011	-23.9	-16.2	-8.6	8.3	11.8	20.3	17.9	16.0	12.7	5.9	-9.7	-15.6	1.6
2012	-21.5	-21.0	-6.3	8.1	11.7	21.3	23.2	18.1	12.4	3.7	-7.3	-25.8	1.4
2013	-18.1	-15.6	-7.9	4.5	9.9	15.2	18.9	17.1	10.1	2.4	-0.6	-9.2	2.2
2014	-17.1	-21.3	-5.1	4.9	11.5	18.4	18.5	18.8	8.3	0.4	-9.1	-12.6	1.3
2015	-15.0	-13.7	-7.9	5.1	13.6	19.8	19.7	16.4	10.0	3.0	-9.0	-7.4	2.9
2016	-22.7	-9.3	-4.2	8.3	12.3	18.6	20.0	18.3	14.1	-1.6	-13.2	-14.8	2.2
2017	-16.1	-15.2	-7.7	5.2	13.1	19.6	19.0	18.0	9.4	1.4	-4.9	-14.0	2.3
2018	-21.7	-17.1	-9.6	3.3	7.3	18.0	19.2	16.4	10.7	4.6	-7.1	-18.8	0.4
2019	-16.8	-18.1	-4.9	3.8	11.4	15.6	20.2	18.7	11.4	5.5	-9.6	-10.5	2.2
2020	-10.8	-8.5	-3.5	9.3	17.8	17.5	20.9	18.9	11.1	4.4	-5.2	-16.6	4.6
2021	-22.2	-17.9	-8.5	2.9	16.2	16.8	19.9	18.3	9.5	3.4	-6.8	-14.3	1.8
2022	-15.1	-12,3

Используя, математические приемы мы рассчитали:

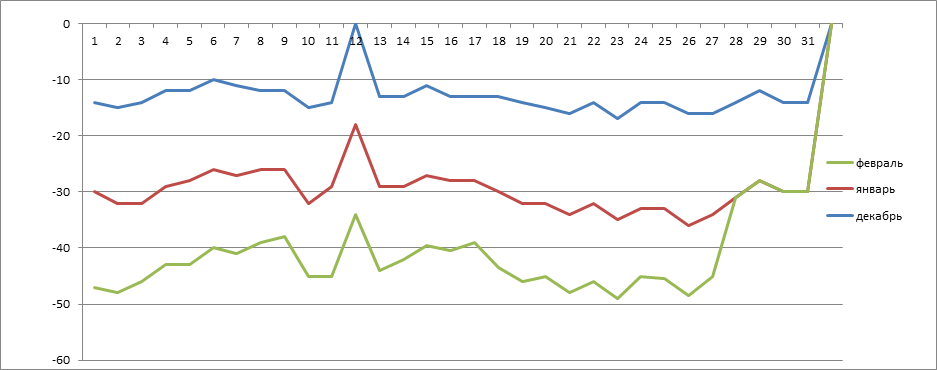
1. Среднесуточную температуру воздуха в январе и феврале по каждому дню - сумма температур за сутки делится на 4, так как было 4 показателя. Пример расчета среднесуточной температуры на 1января:(-17⁰+(-15⁰)+(-10⁰)+(-14⁰)) :4= -14⁰; на 1 февраля : (-17⁰ + (-16⁰) + (-14⁰)+(-13⁰)): 4 = -15⁰, и так по каждому дню. По полученным данным мы определили, что самый теплый день в январе выдался на 8 число (-12⁰С), а самый холодный – на 26 число (-22⁰С). В декабре тепло было 6 числа

(-8⁰С), а холодно 22 и 26 (-15⁰С).В феврале самый теплый день 28 числа (-8⁰С), а свмый холодный1февраля (-15⁰).  Из трех зимних месяцев самым холодным стал январь, особенно 3 декада. (Приложения 1,2);

		1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21	22	23	24	25	26	27	28	29	30	31
декабрь	Д.т	-12	-13	-12	-10	-10	-8	-9	-9	-9	-13	-13	-12	-11	-11	-10	-11	-11	-11	-12	-13	-14	-15	-14	-13	-13	-15	-14	-14	-11	-9	-13
	Н.т	-16	-17	-17	-14	-14	-13	-13	-14	-13	-18	-16	-16	-15	-15	-13	-15	-15	-15	-16	-17	-19	-18	-19	-16	-16	-18	-18	-19	-17	-14	-15
январь	Д.т	-14	-15	-16	-16	-15	-14	-14	-12	-12	-15	-13	-16	-14	-14	-14	-12	-12	-15	-15	-16	-15	-15	-15	-17	-17	-17	-15	-15	-15	-15	-15
	Н.т	-19	-19	-20	-20	-19	-18	-18	-16	-16	-19	-17	-20	-18	-19	-18	-17	-17	-18	-20	-20	-20	-19	-20	-20	-21	-22	-21	-19	-18	-17	-19
февраль	Д.т	-15	-14	-12	-12	-13	-11	-10	-10	-11	-12	-15	-14	-13	-11	-10	-9	-9	-12	-11	-11	-12	-12	-12	-10	-11	-11	-9	-8
	Н.т	-20	-19	-17	-16	-17	-16	-17	-15	-13	-15	-19	-19	-15	-16	-15	-14	-13	-15	-17	-15	-16	-16	-16	-14	-14	-14	-14	-13

 

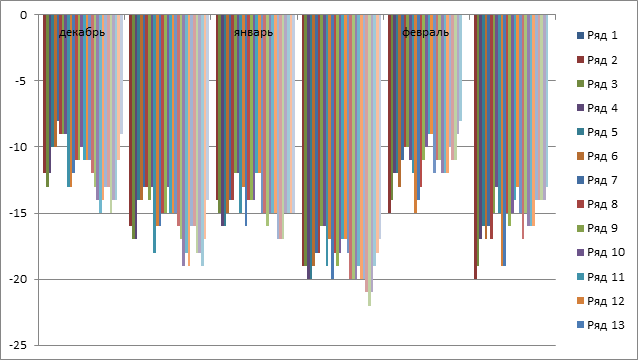
2. Среднемесячную температуру воздуха в декабре, январе и феврале (сумма среднесуточных температур делится на количество дней в месяце), которая составила: --10,4⁰С, -15,1⁰С и –12,3⁰С соответственно. Примет расчета среднемесячной температуры воздуха за декабрь: (суммируется среднесуточная, округленная до целого числа, температура): 31(количество дней в месяце) = -14,3⁰С. Мы сравнили эти данные с температурной нормой за 2020гг. и выяснили, что декабрь оказался теплее на 1,7⁰С а декабрь (норма -16⁰С).

3. Амплитуду температур (разность между высокой и низкой температурой). Амплитуда определяется по формуле:

А = tВ – tН

А – амплитуда, tВ – высокая температура, tН - низкая температура.

Расчет амплитуды температур в декабре:

А = -8⁰ – (-19⁰) = -11⁰

Расчет амплитуды температур в январе:

А = - 12⁰ – (-22⁰) = -10⁰.

Расчет амплитуды температур в феврале:

А = - 8⁰ – (-20⁰) = -12⁰.

 

По этим данным можно сравнить температурный режим в декабре, январе и феврале и сравнить с показаниями других годов.

Сравнить среднесуточную температуры в декабре, январе и феврале 2020г. наглядно можно при построении диаграммы.

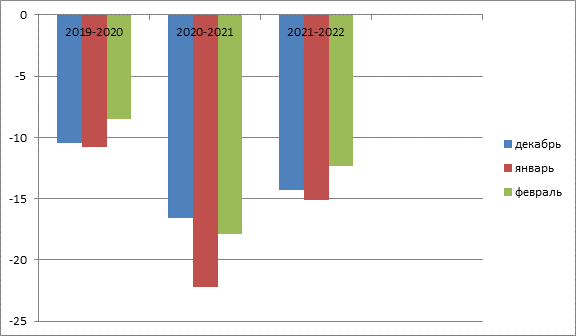
Анализируя среднемесячные температуры данные  за несколько лет можно сказать, что зима у нас длиться 5 месяцев, весна- осень  по 2  месяца, лето-3 месяца. Наш район расположен  в зоне континентального климата, характеризующегося значительными колебаниями сезонных температур., а также дневных и ночных температур.

 

 

 

 

 

 

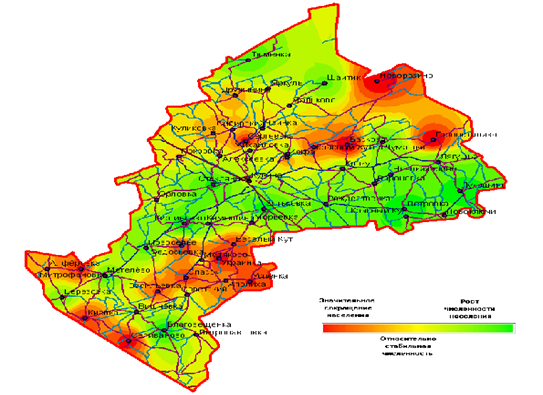
 2.4   Плотность населения Купинского района.

Плотность населения – это величина, показывающая, сколько человек проживает на 1 кв. км. данной территории.

Чтобы посчитать плотность населения, нужно количество населения разделить на площадь территории. Пл=К:S, где К – количество жителей. S – площадь территории.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

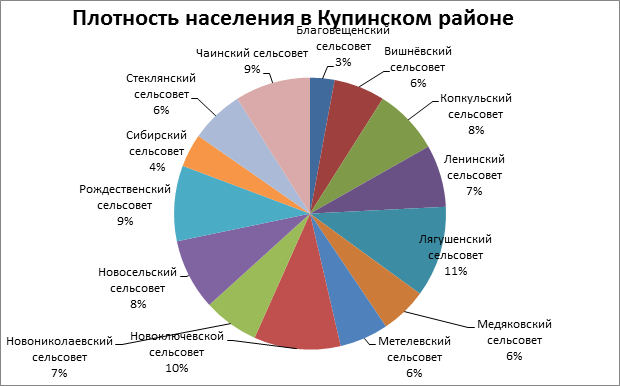
Купинский район -это равнина, усеянная небольшими озерами. Плотность населения связана с плодородием земли и озерной системой.

Заключение

Математика и география – это две науки, которые не могут существовать друг без друга, они неразрывно связаны между собой, и продолжают работать вместе на благо всего человечества.

Проведенный анализ литературы и числовых данных, полученных в результате наблюдения за температурой воздуха, показателями плотности населения, географической широтой, масштабом показал, что математические приемы помогают более глубоко анализировать географические явления. В  работе  использовались следующие математические величины, операции, приемы, изображения: нахождение среднеарифметического значения, округление до целого числа, сравнение чисел, построение диаграмм. На небольшом примере мы рассмотрели взаимосвязь между двумя великими науками математика и география. Эта взаимосвязь проявляется во многих географических темах.

Таким образом, в ходе работы нами были достигнуты цели и задачи исследования, подтверждена рабочая гипотеза о том, что математика и география тесно связаны между собой.

 

Список источников информации

1.      Алексеев А.И., Николина В.В. География. 5-6 классы: учеб. для общеобразовательных организаций. – М.: Просвещение, 2015. – 191с.

2.      Маркушевич А.Г. Детская энциклопедия. Том 3. – М.: Академия Педагогических Наук РСФСР, 1958. – 709 с.

3.      Орлов Б.П. Детская энциклопедия. Том 1. – М.: Академия Педагогических Наук РСФСР, 1958. – 586с.

4.      Савин А.П. Энциклопедический словарь юного математика. – М.: Педагогика, 1989. – 352 с.

5.      Трешников А.Ф. Географический энциклопедический словарь. Понятия и термины. – М.: Советская энциклопедия, 1988. – 432с.

6.      Энциклопедия. География. Т.3.-М. :Аванта+ 1997.-704 с.

7.      Мини- энциклопедия. Справочник. –М. 2002. -1100с.

8.      Математика в твоих руках. Калинина А.Б.-М.2016г.

9.      Из истории математики И.Я. Депман –М 2013г.-84с.

10.  Математика история идей и открытий И. Рыбаков 1988-76с

11.  География [Электронный ресурс] – Режим доступа: https://geografiyazemli.ru/

12.  Как появилась математика: основы и история развития науки. Роль математики в жизни и интересные факты [Электронный ресурс] – Режим доступа: http://fb.ru/article/400486/kak-poyavilas-matematika-osnovyi-i-istoriya-razvitiya-nauki-rol-matematiki-v-jizni-i-interesnyie-faktyi

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

		1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21	22	23	24	25	26	27	28	29	30	31
декабрь		-12	-13	-12	-10	-10	-8	-9	-9	-9	-13	-13	-12	-11	-11	-10	-11	-11	-11	-12	-13	-14	-15	-14	-13	-13	-15	-14	-14	-11	-9	-13
	Н.т	-16	-17	-17	-14	-14	-13	-13	-14	-13	-18	-16	-16	-15	-15	-13	-15	-15	-15	-16	-17	-19	-18	-19	-16	-16	-18	-18	-19	-17	-14	-15
январь	Д.т	-14	-15	-16	-16	-15	-14	-14	-12	-12	-15	-13	-16	-14	-14	-14	-12	-12	-15	-15	-16	-15	-15	-15	-17	-17	-17	-15	-15	-15	-15	-15
	Н.т	-19	-19	-20	-20	-19	-18	-18	-16	-16	-19	-17	-20	-18	-19	-18	-17	-17	-18	-20	-20	-20	-19	-20	-20	-21	-22	-21	-19	-18	-17	-19
февраль	Д.т	-15	-14	-12	-12	-13	-11	-10	-10	-11	-12	-15	-14	-13	-11	-10	-9	-9	-12	-11	-11	-12	-12	-12	-10	-11	-11	-9	-8
	Н.т	-20	-19	-17	-16	-17	-16	-17	-15	-13	-15	-19	-19	-15	-16	-15	-14	-13	-15	-17	-15	-16	-16	-16	-14	-14	-14	-14	-13

 

 

 

 

 

 

 

 

 

 

 

 

Скачано с www.znanio.ru