Расстояние между прямыми, расстояние от точки до плоскости.

Балинова Елена Васильевна,

учитель математики, высшая КК,

МБОУ «Пинежская СШ № 117»

п. Пинега, Архангельской области

МЕТОД КООРДИНАТ: РАССТОЯНИЕ МЕЖДУ ПРЯМЫМИ, РАССТОЯНИЕ ОТ ТОЧКИ ДО ПЛОСКОСТИ.

В последние несколько лет учащимся на ЕГЭ предлагаются задачи на нахождение  расстояния между прямыми и расстояние от точки до плоскости. Их можно решить разными способами. Способ «Метод координат»  является дополнением  к школьному учебнику «Геометрия – 10-11» и предназначен для организации решения задач учащимися на уроке после их ознакомления вычисления угла между прямыми. Своих учеников знакомлю с новым методом решения задач  на нахождение  расстояния между прямыми и расстояние от точки до прямой, что намного облегчает решение таких задач, так как применяется одна формула. Вначале повторяются задания на нахождение основных (необходимых) для решения задач элементов.

Нахождение координат точек многоугольников, многогранников и тел вращения доводим до автоматизма. Для этого многогранник помещаю в систему координат, меняя  начало координат в вершинах многогранника. Кроме этого, отрабатываю нахождение координат точек у правильных фигур плоскости (треугольник, квадрат и шестиугольник), так как они чаще используются в решении задач.

После повторения  решаем задачу с подробным описанием решения. На этом этапе учащиеся делают первые шаги по осознанию нового материала, освоению основных действий с изучаемым материалом. Для этого подробно разбираем новый материал и выводим алгоритм решения задач. Рассмотрим способ вычисления расстояния между прямыми и расстояние от точки до плоскости.

Алгоритм нахождения  расстояния:

1. На рисунке изображаем указанные в задаче прямые (которым придаем направление, т.е. вектора).

2. Вписываем фигуру в систему координат.

3. Находим координаты точек, необходимых для получения уравнения плоскости.

4. Составляем уравнение плоскости .

5. Находим координаты вектора нормали плоскости.

6. Подставляем в формулу                                                 ,  где  М₀(х₀, у₀, z₀)  данная точка.

Задача № 1

В прямоугольном параллелепипеде ABCDA₁B₁C₁D₁ , все ребра которого равны 1, найдите  расстояние между прямыми А₁В   и D₁B₁.

Решение:

Нахождение расстояния между прямыми сведем к расстоянию от точки до плоскости. Плоскость необходимо построить. Она будет параллельна каждой из этих прямых. При этом желательно, чтобы она проходила через одну из этих прямых (допустим через ВА₁).

1.      Найдем координаты точек В (1; 1; 0),   В ₁ (1; 1; 1),   А₁ (1; 0; 1),   D₁ (0; 0; 1)

2.      Найдем направляющие векторы этих прямых  ВА₁ {0 ; -1 ; 1},  B₁D₁ {-1 ; -1 ; 1}, 

3.      Зададим вектор между точкой М {x ; y ; z}

и любой точкой, например точкой В (1; 1; 0), получим вектор ВМ {x-1 ; y-1 ; z}. 

4.      Составим  матрицу из этих векторов и получим уравнение плоскости.

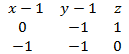      = (x-1) · 1· 0 + 0· (-1) · z -1 · (y-1) ·1 – z· (-1) · (-1) – 1· (-1) · (x-1) –            -  0 ·(x-1)· 0 = x-y-z

Получаем уравнение плоскости       x-y-z = 0

Вычислим расстояние между прямыми по формуле  расстояния от точки В (1; 1; 0) до плоскости, заданной уравнением А x+ Вy + Сz + D = 0, где координаты вектора –нормали  {А; В; С}   т. е. {1; -1; -1}

 (d =      D = 1 так как пплоскость не проходит через начало координат.

d =  =    =   =      =.  Ответ:

Рассмотрим задачу из материалов ЕГЭ.

Задача № 14 (ЕГЭ 2016г).

В правильной четырехугольной призме ABCDA₁B₁C₁D₁сторона АВ основания равна 8, а боковое ребро АА₁  равно 4√2. На ребрах ВС и С₁D₁ отмечены точки K и L соответственно, причем BK = C₁L = 2. Плоскость α параллельна прямой BD и содержит точки K и L.  Найдите расстояние о точки В до плоскости γ.

Решим задачу методом координат.

Поместим четырехугольную призму ABCDA₁B₁C₁D₁ в декартовую систему координат с центром в точке D(0;0;0)

а) 1) Найдем координаты точек  K₁(0; 2 0) L(0; 6; 4) L₁(2; 8; 4) Составим уравнение плоскости с помощью системы уравнений.

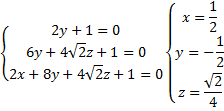
Тогда координаты вектора нормали {; -; },

длина вектора нормали   ==.

1)   Найдем координаты точек A₁(8; 0; 4) С(0; 8; 0) и координаты вектора 

A₁C{8; -8; 4) 

3) Вычислим угол между прямой и плоскостью
= =1, отсюда следует: угол  равен 90⁰. Значит, прямая A₁C перпендикулярна плоскости γ.

б) 1) Координаты точки В(8; 8; 0), тогда расстояние от точки В будет 
d =  =  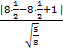= =        Ответ: б) 

Чтобы отработать алгоритм решения задач, учащимся предлагается набор дополнительных задач разного уровня сложности. При этом ученик может выбрать многогранник: куб, призму или пирамиду. Учитель осуществляет во время занятия оперативный контроль и коррекцию деятельности учащихся.

Расстояние между прямыми в пространстве.

Расстояние между двумя непересекающимися прямыми в пространстве называется длина общего перпендикуляра, проведенного к этим прямым.

Уровень А

1)      В единичном кубе A…D₁найдите расстояние между прямыми ABи CD.

2)      В единичном кубе A…D₁найдите расстояние между прямыми AB и A₁B₁.

3)      В единичном кубе A…D₁найдите расстояние между прямымиAB и CC₁.

4)      В правильной четырех угольной пирамиде SABCD, все ребра которой равны 1, найдите расстояние между прямыми ABи CD.

5)      В правильной треугольной призме ABCA₁B₁C₁, все ребра которой равны 1, найдите расстояние между прямыми ACи A₁C₁.

6)      В правильной шестиугольной призме A…F₁, все ребра которой равны 1, найдите расстояние между прямыми AA₁и BB₁.

7)      В правильной шестиугольной пирамиде SABCDEF, стороны основания которой равны 1, найдите расстояние между прямыми BD и AE.
Ответы:   1)1 2)1 3)1 4)1 5)1 6)1 7)1

Уровень В

1)      В единичном кубе A…D₁найдите расстояние между прямыми AB и CD₁.

2)      В единичном кубе A…D₁найдите расстояние между прямыми AB и DC₁.

3)      В единичном кубе A…D₁найдите расстояние между прямыми AB и A₁C₁.

4)      В правильной шестиугольной пирамиде SABCDEF, стороны которой равны √3, найдите расстояние между прямыми BCи EF.

5)      В правильной треугольной призме ABCA₁B₁С₁, все ребра которой равны 1, найдите расстояние между прямыми AB и B₁C₁.

6)      В правильной шестиугольной призме A…F₁, все ребра которой равны 1, найдите расстояние между прямыми BC и D₁E_1.
Ответы:
1)1 2)1 3)1 4)3 5)1 6)1

Скачано с www.znanio.ru