
Задания 27 метод DBSCAN
Для решения 27 задания есть несколько методов:
Метод кластеризации подразумевает что в первую очередь необходимо узнать сколько всего кластеров, это можно узнать с помощью электронной таблицы – Эксель, после разделить кластеры с помощью уравнений.
Метод К-средних дает приблизительные значения поэтому этот метод не подходить для решения 27 задания.
Методе DBSCAN не нужно узнавать сколько кластеров и разделять эти кластеры с помощью уравнений. DBSCAN самостоятельно разделяет точки на кластеры.
-------------------------------------------------------------------------------------------------------------
Во время работы с файлами необходимо понимать, что Python работает с вещественными числами только точкой, например:
Число 8,31 Python не понимает, как с этим работать, поэтому запятую заменяем на точку с помощью функции replace(‘,’, ’.’).
Поэтому на экзамене файлы с данными, то есть числами могут попасться так и с запятыми так и с точками.
ЧТОБЫ ЛУЧШЕ ПОНЯТЬ ЭТИ МЕТОДЫ РЕКОМЕНДУЮ ПОСМОТРЕТЬ СЛЕДУЮЩИЕ ВИДЕО:
1) https://youtu.be/TjZtxwkVoWU?si=tP2w-fKqohTc1WoA
2) https://youtu.be/88yThM_kxQI?si=Bt5Fuq5NWyOHXNIJ
3) https://youtu.be/IGGt9bqi5Ss?si=SVZOn8eiEpNxErAE
4) https://rutube.ru/video/cb3160dd13c74933be5a086d50d7171d/
5) https://www.youtube.com/watch?v=QHqUCVI80XE&t=23s
6) https://www.youtube.com/watch?v=jTytrUQT-Ew
7) https://www.youtube.com/watch?v=aJuVDirgEXg&t=2275s
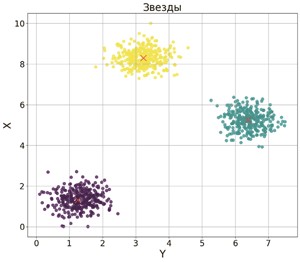
27) (№ 7581) (Демо-2025) Учёный решил провести кластеризацию некоторого множества звёзд по их расположению на карте звёздного неба. Кластер звёзд – это набор звёзд (точек) на графике. Каждая звезда обязательно принадлежит только одному из кластеров. Центр кластера, или центроид, – это одна из звёзд на графике, сумма расстояний от которой до всех остальных звёзд кластера минимальна. Расстояние между двумя точками A(x1, y1) и B(x2, y2) вычисляется по формуле:
![]() Даны два входных файла (файл A и файл Б). В файле A
Даны два входных файла (файл A и файл Б). В файле A
хранятся данные о звёздах двух кластеров. В каждой строке записана информация о расположении на карте одной звезды: сначала координата x, затем координата y (в условных единицах). Известно, что количество звёзд не превышает 1000. В файле Б хранятся данные о звёздах трёх кластеров. Известно, что количество звёзд не превышает 10 000. Структура хранения информации о звездах в файле Б аналогична файлу А. Возможные данные одного из файлов иллюстрированы графиком.
Для каждого файла определите координаты центра каждого кластера, затем вычислите два числа: Px – среднее арифметическое абсцисс центров кластеров, и Py – среднее арифметическое ординат центров кластеров. В ответе запишите четыре числа: в первой строке сначала целую часть произведения Px×10 000, затем целую часть произведения Py×10 000 для файла А, во второй строке – аналогичные данные для файла Б.
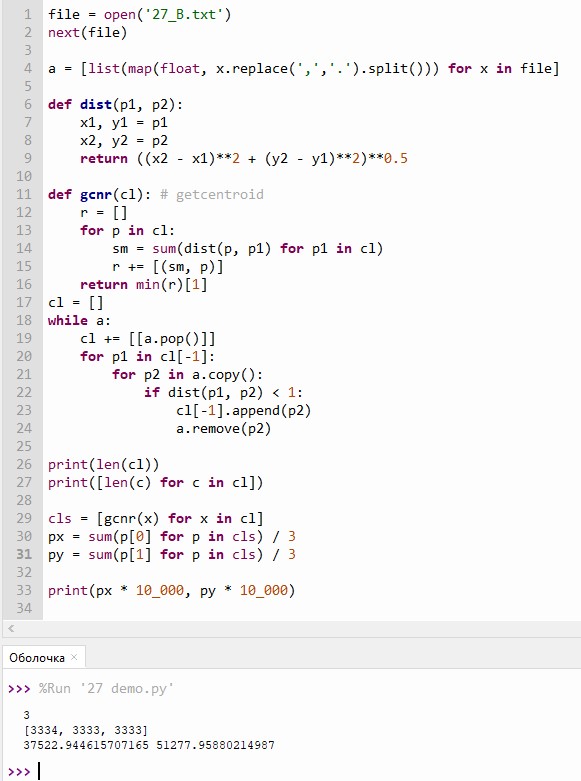
Решение:
Прежде чем найти ответы лучше прописать команды в строке 26 и 27, чтобы узнать сколько кластеров, это пригодится если в задании будут аномалии.
Количество кластеров: print(len(cl))
Количество точек в кластерах: print([len(c) for c in cl])
Файл А

Файл Б
Ответ:
10738 30730
37522 51277
|
file = open('27_A.txt') next(file)
a = [list(map(float, x.replace(',','.').split())) for x in file]
def dist(p1, p2): x1, y1 = p1 x2, y2 = p2 return ((x2 - x1)**2 + (y2 - y1)**2)**0.5
def gcnr(cl): # getcentroid r = [] for p in cl: sm = sum(dist(p, p1) for p1 in cl) r += [(sm, p)] return min(r)[1] cl = [] while a: cl += [[a.pop()]] for p1 in cl[-1]: for p2 in a.copy(): if dist(p1, p2) < 1: cl[-1].append(p2) a.remove(p2)
cls = [gcnr(x) for x in cl] px = sum(p[0] for p in cls) / 2 py = sum(p[1] for p in cls) / 2 print(px * 10_000, py * 10_000)
|
Файл А два кластера
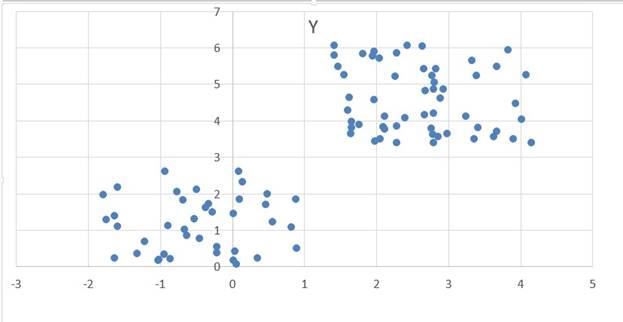
Файл Б три кластера

27) (№ 7644) (В. Шубинкин) В ходе эксперимента были зафиксированы очаги радиации. Чтобы изучить данное явление, решили провести кластеризацию источников излучения. Кластер – это набор источников (точек) на графике, лежащий внутри прямоугольника высотой H и шириной W. Каждая точка обязательно принадлежит только одному из кластеров. Истинный центр кластера, или центроид, – это одна из точек на графике, сумма расстояний от которой до всех остальных точек кластера минимальна. Расстояние между двумя точками A(x1, y1) и B(x2, y2) вычисляется по формуле:
![]() Аномалиями назовём совокупности из
не более
Аномалиями назовём совокупности из
не более
чем 10 точек, каждая из которых находится на расстоянии более одной условной единицы от точек кластеров. Аномалии в расчётах не учитываются. Даны два входных файла (файл A и файл Б). В файле A хранятся данные о точках двух кластеров. В каждой строке записана информация о расположении одной точки: сначала координата x, затем координата y (в условных единицах). Известно, что количество точек не превышает 1000. В файле Б той же структуры хранятся данные о трёх кластерах. Известно, что количество точек не превышает 10 000. Структура хранения информации о точках в файле Б аналогична файлу А. Возможные данные одного из файлов иллюстрированы графиком.
Для каждого файла определите координаты центра каждого кластера, затем вычислите два числа: Px – среднее арифметическое абсцисс центров кластеров, и Py – среднее арифметическое ординат центров кластеров. В ответе запишите четыре числа: в первой строке сначала целую часть произведения Px×100 000, затем целую часть произведения Py×100 000 для файла А, во второй строке – аналогичные данные для файла Б.
Решение:
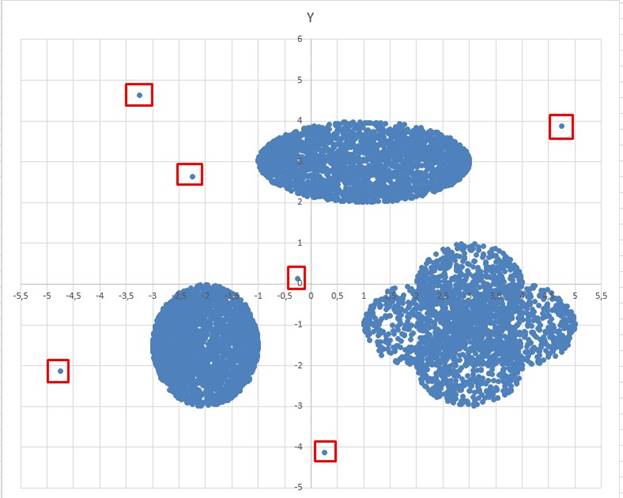
В файле А визуально видим 6 аномалий и 2 кластера, метод dbscan посчитает их как отдельные кластеры, эти аномалии по условию учитывать не нужно. Поэтому когда находится центроиды
cls = [gcnr(x) for x in cl if len(x) > 30]
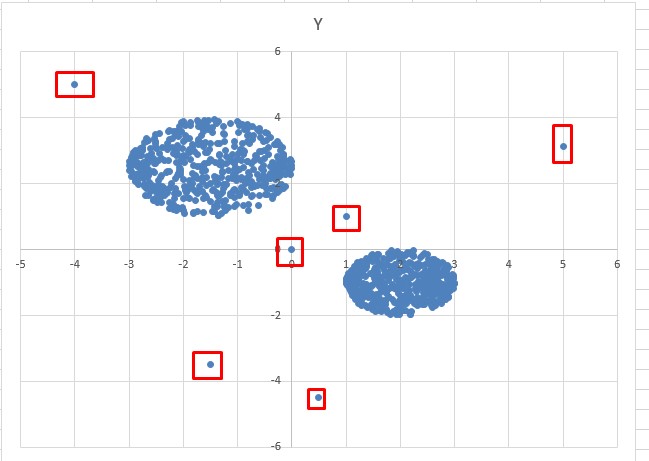
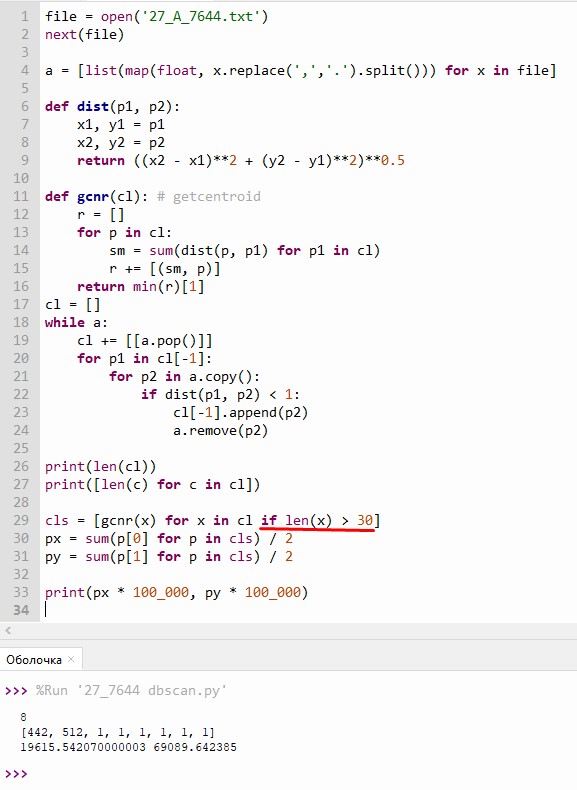
В файле Б также 6 аномалий и 3 кластера.
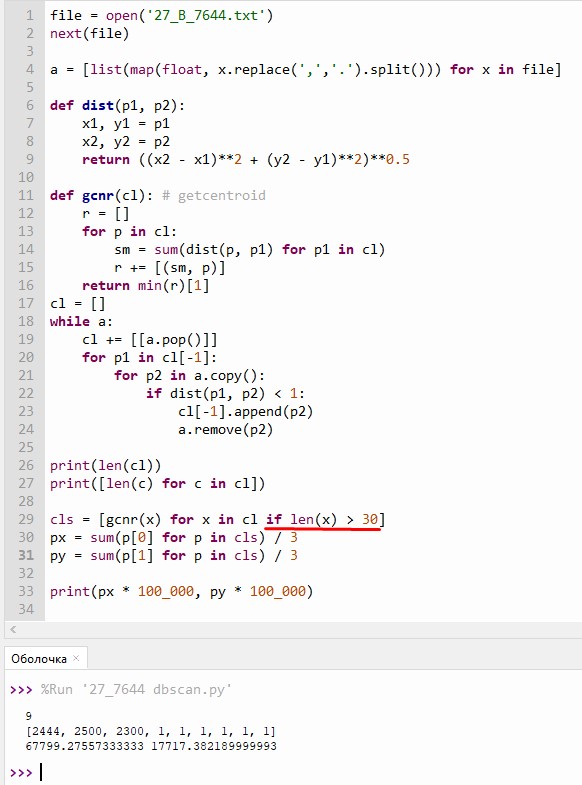
Ответ:
19615 69089
67799 17717
(№ 7651) (В. Ланская, Р. Ягафаров) Учёный решил провести кластеризацию некоторого множества звёзд по их расположению на карте звёздного неба. Кластер звёзд – это набор звёзд (точек) на графике. Каждая звезда обязательно принадлежит только одному из кластеров. Центр кластера, или центроид, – это одна из звёзд на графике, сумма расстояний от которой до всех остальных звёзд кластера минимальна. Расстояние между двумя точками A(x1, y1) и B(x2, y2) вычисляется по формуле:
![]()
Даны два входных файла (файл A и файл Б). В файле A хранятся данные о звёздах двух кластеров. В каждой строке записана информация о расположении на карте одной звезды: сначала координата x, затем координата y (в условных единицах). Известно, что количество звёзд не превышает 1000. В файле Б хранятся данные о звёздах четырёх кластеров. Известно, что количество звёзд не превышает 10 000. Структура хранения информации о звездах в файле Б аналогична файлу А. Возможные данные одного из файлов иллюстрированы графиком.
Для каждого файла определите координаты центра каждого кластера, затем вычислите два числа: Px – среднее арифметическое абсцисс центров кластеров, и Py – среднее арифметическое ординат центров кластеров. В ответе запишите четыре числа: в первой строке сначала целую часть произведения Px×10 000, затем целую часть произведения Py×10 000 для файла А, во второй строке – аналогичные данные для файла Б.
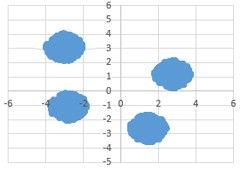
Решение
Файла А два кластера
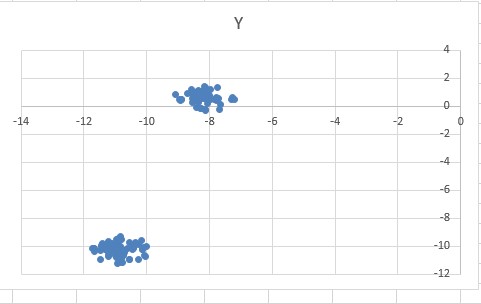
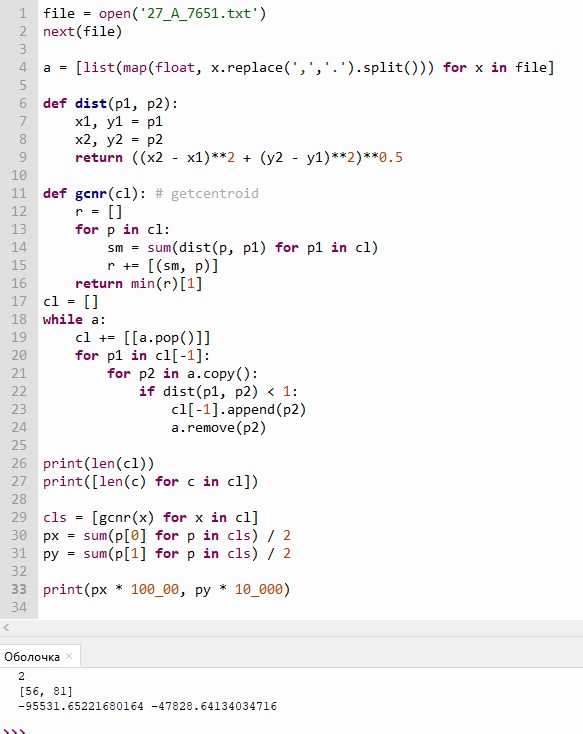
Файл Б четыре кластера
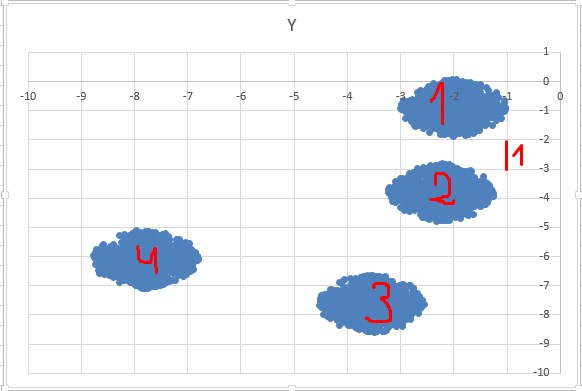
Визуально видим 4 кластера, но метод DBSCAN показывает 3 кластера
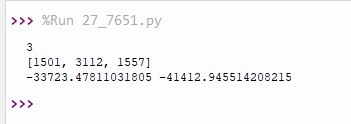
Это из-за того что растояние между первым и вторым кластером меньше чем единица.
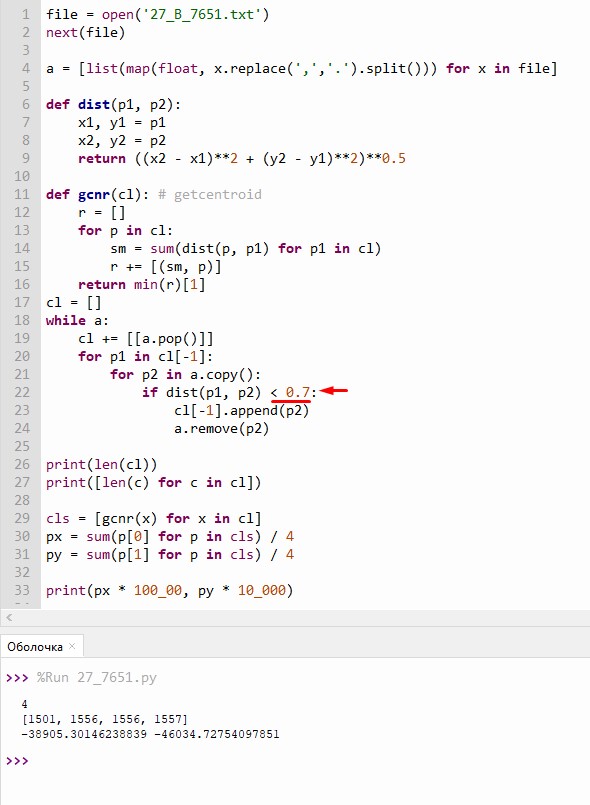
Ответ:
-95531 -47828
-38905 -46034
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.