19 – 21. Теория игр.

В задачах 19 – 21 может попасться ОДНА КУЧА или ДВЕ КУЧИ.

Одна куча если попадется стандартная задача, то можно решить задачу руками, но проверить написав программу будет лучше.

Две кучи руками решать сложнее, поэтому лучше написать программу.

Шаблон ОДНА КУЧА

def f(x, m):     if x >= 273:

        return m % 2 == 0     if m == 0:         return 0

    h = [f(x+2, m-1), f(x+5, m-1), f(x*4, m-1)]     return any(h) if (m-1) % 2 == 0 else all(h) print('19)', [s for s in range(1, 273) if f(s, 2)]) print('20)', [s for s in range(1, 273) if not f(s, 1) and f(s, 3)]) print('21)', [s for s in range(1, 273) if not f(s, 2) and f(s, 4)])

Шаблон ДВЕ КУЧИ

def f(x, y, m):

    if x+y >= 75:

        return m % 2 == 0     if m == 0:         return 0     h = [f(x+1, y, m-1), f(x, y+1, m-1), f(x+y, y, m-1), f(x, y+x, m-1)]     return any(h) if (m-1) % 2 == 0 else all(h) print('19)', [s for s in range(1, 75) if f(7, s, 2)]) print('20)', [s for s in range(1, 75) if not f(7, s, 1) and f(7, s, 3)]) print('21)', [s for s in range(1, 75) if not f(7, s, 2) and f(7, s, 4)]) № 13084 (KOMPEGE)

Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежит куча камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в кучу один камень, увеличить количество камней в куче в два раза, если оно нечётное, или в полтора раза, если оно чётное.

Например, если в куче 5 камней, то за один ход можно получить 6 или 10 камней, а если в куче 6 камней, то за один ход можно получить 7 или 9 камней.

Игра завершается, когда количество камней в куче достигает 84. Победителем считается игрок, сделавший последний ход, то есть первым получивший кучу, в которой будет 84 или больше камней.

В начале игры в куче было S камней, 1 ≤ S ≤ 83

Укажите максимальное значение S, при котором Петя не может выиграть первым ходом, но при любом первом ходе Пети Ваня может выиграть своим первым ходом.

Задание 20.

Для игры, описанной в задании 19, найдите два наименьших значения S, при которых Петя не может выиграть первым ходом, но у Пети есть выигрышная стратегия, позволяющая ему выиграть вторым ходом при любой игре Вани.

В ответе запишите найденные значения в порядке возрастания.

Задание 21.

Для игры, описанной в задании 19, найдите максимальное значение S, при котором у Вани есть стратегия, позволяющая ему выиграть первым или вторым ходом при любой игре Пети, но у Вани нет стратегии, которая позволила бы ему гарантированно выиграть первым ходом.

Ответ:

19)   54

20)   21 23

21)   40

Решение: Задачу решать руками будет сложнее, поэтому лучше написать программу

def f(x, m):     if x >= 84:

        return m % 2 == 0     if m == 0:         return 0     h = [f(x+1, m-1)]     if x % 2 == 1:

        h += [f(x*2, m-1)]     if x % 2 == 0:

        h += [f(x*1.5, m-1)]

    return any(h) if (m-1) % 2 == 0 else all(h) print('19)', [s for s in range(1, 84) if f(s, 2)]) print('20)', [s for s in range(1, 84) if not f(s, 1) and f(s, 3)]) print('21)', [s for s in range(1, 84) if not f(s, 2) and f(s, 4)])

Результат выполнения программы:

19)  [42, 44, 46, 48, 50, 52, 54]             # max: 54

20)  [21, 23, 25, 27, 28, 32, 36, 41]       # min: 21 23

21)  [24, 31, 35, 40]                                 # max: 40

№ 12251 (KOMPEGE)  

Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежит куча камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в кучу три камня либо увеличить количество камней в куче в пять раз. Для того чтобы делать ходы, у каждого игрока есть неограниченное количество камней.

Игра завершается в тот момент, когда количество камней в куче становится не менее 301. Победителем считается игрок, сделавший последний ход, т.е. первым получивший кучу, состоящую из 301 или более камней. В начальный момент в куче было S камней; 1 ≤ S ≤ 300. Будем говорить, что игрок имеет выигрышную стратегию, если он может выиграть при любых ходах противника.

Укажите наименьшее значение S, при котором Петя не может выиграть за один ход, но при любом ходе Пети Ваня может выиграть своим первым ходом.

Задание 20.

Для игры, описанной в задании 19, найдите два наименьших значения S, при которых у Пети есть выигрышная стратегия, причём одновременно выполняются два условия:

–  Петя не может выиграть за один ход;

–  Петя может выиграть своим вторым ходом независимо от того, как будет ходить Ваня. Найденные значения запишите в ответе в порядке возрастания. 

Задание 21.

Для игры, описанной в задании 19, найдите минимальное значение S, при котором одновременно выполняются два условия:

–  у Вани есть выигрышная стратегия, позволяющая ему выиграть первым или вторым ходом при любой игре Пети;

–  у Вани нет стратегии, которая позволит ему гарантированно выиграть первым ходом.

Если найдено несколько значений S, в ответе запишите минимальное из них

Ответ:

19)   58

20)   11 55

21)   52

Решение: Задачу решать руками будет сложнее, поэтому лучше написать программу

def f(x, m):     if x >= 301:

        return m % 2 == 0     if m == 0:         return 0

    h = [f(x+3, m-1), f(x*5, m-1)]

    return any(h) if (m-1) % 2 == 0 else all(h) print('19)', [s for s in range(1, 301) if f(s, 2)]) print('20)', [s for s in range(1, 301) if not f(s, 1) and f(s, 3)]) print('21)', [s for s in range(1, 301) if not f(s, 2) and f(s, 4)])

Результат выполнения программы:

19)  [58, 59, 60]             # min: 58

20)  [12, 55, 56, 57]      # min: 12 55

21)  [52, 53, 54]            #  min 52

№ 27808 (Решу Егэ)  

Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежит куча камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в кучу один или три камня или увеличить количество камней в куче в два раза. Например, имея кучу из 15 камней, за один ход можно получить кучу из 16, 18 или 30 камней. У каждого игрока, чтобы делать ходы, есть неограниченное количество камней.

Игра завершается в тот момент, когда количество камней в куче становится не менее 42. Победителем считается игрок, сделавший последний ход, т. е. первым получивший кучу, в которой будет 42 или больше камней.  В начальный момент в куче было S камней;    

Будем говорить, что игрок имеет выигрышную стратегию, если он может выиграть при любых ходах противника. Описать стратегию игрока — значит, описать, какой ход он должен сделать в любой ситуации, которая ему может встретиться при различной игре противника. В описание выигрышной стратегии не следует включать ходы играющего по этой стратегии игрока, не являющиеся для него безусловно выигрышными, т. е. не являющиеся выигрышными независимо от игры противника.

Известно, что Ваня выиграл своим первым ходом после неудачного первого хода Пети. Укажите минимальное значение S, когда такая ситуация возможна. Задание 20. 

Найдите три таких значения S, при которых у Пети есть выигрышная стратегия, причём одновременно выполняются два условия:

— Петя не может выиграть за один ход;

— Петя может выиграть своим вторым ходом независимо от того, как будет ходить Ваня.

Найденные значения запишите в ответе в порядке возрастания без разделительных знаков.

Задание 21. 

Найдите минимальное значение S, при котором одновременно выполняются два условия: — у Вани есть выигрышная стратегия, позволяющая ему выиграть первым или вторым ходом при любой игре Пети;

— у Вани нет стратегии, которая позволит ему гарантированно выиграть первым ходом.

Ответ:

19)  11

20)  10 17 19

21)  16

Решение: задачу можно решать руками построив дерево, но написать программу для проверки лучше. 

19) Петя сделал неудачный ход, поэтому, 42 делим дважды на 2: 42 / 2 / 2 = 10,5. В 19 задании получившийся ответ увеличиваем в большую сторону, то есть ответ 11.  

Если в условии сказано было бы при любом ходе Пети, то будет ответ 20

В 20 и 21 заданиях получившийся ответ уменьшаем в меньшею сторону при делении. def f(x, m):     if x >= 42:

        return m % 2 == 0     if m == 0:         return 0

    h = [f(x+1, m-1), f(x+3, m-1), f(x*2, m-1)]     return any(h) if (m-1) % 2 == 0 else all(h)

print('19)', [s for s in range(1, 42) if f(s, 2)])

print('20)', [s for s in range(1, 42) if not f(s, 1) and f(s, 3)]) print('21)', [s for s in range(1, 42) if not f(s, 2) and f(s, 4)])

19)  [11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31,

32, 33, 34, 35, 36, 37, 38, 39, 40]

20)  [10, 17, 19]

21)  [16, 18]

№ 27932 (Решу Егэ)  

Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежит куча камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в кучу один или два камня или увеличить количество камней в куче в три раза. Например, имея кучу из 15 камней, за один ход можно получить кучу из 16, 17 или 45 камней. У каждого игрока, чтобы делать ходы, есть неограниченное количество камней. Игра завершается в тот момент, когда количество камней в куче становится не менее 76. Победителем считается игрок, сделавший последний ход, то есть первым получивший кучу, в которой будет 76 или больше камней. В начальный момент в куче было S камней, 1 ≤ S ≤ 75.

Будем говорить, что игрок имеет выигрышную стратегию, если он может выиграть при любых ходах противника. Описать стратегию игрока  — значит, описать, какой ход он должен сделать в любой ситуации, которая ему может встретиться при различной игре противника.

Известно, что Ваня выиграл своим первым ходом после неудачного первого хода Пети. Укажите минимальное значение S, когда такая ситуация возможна.

Задание 20.

Найдите два таких значения S, при которых у Пети есть выигрышная стратегия, причём одновременно выполняются два условия:

— Петя не может выиграть за один ход;

— Петя может выиграть своим вторым ходом независимо от того, как будет ходить Ваня. Найденные значения запишите в ответе в порядке возрастания без разделительных знаков.

Задание 21.

Найдите минимальное значение S, при котором одновременно выполняются два условия: — у Вани есть выигрышная стратегия, позволяющая ему выиграть первым или вторым ходом при любой игре Пети; — у Вани нет стратегии, которая позволит ему гарантированно выиграть первым ходом.

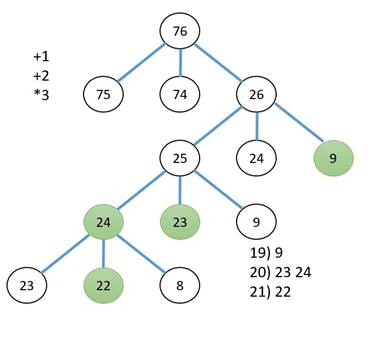
19)   9

20)   23 24

21)   22

Решение: задачу можно решать руками построив дерево, но написать программу для проверки лучше. 

def f(x, m):     if x >= 76:

        return m % 2 == 0     if m == 0:         return 0

    h = [f(x+1, m-1), f(x+2, m-1), f(x*3, m-1)]

    return any(h) if (m-1) % 2 == 0 else all(h)

print('19)', [s for s in range(1, 76) if f(s, 2)]) print('20)', [s for s in range(1, 76) if not f(s, 1) and f(s, 3)]) print('21)', [s for s in range(1, 76) if not f(s, 2) and f(s, 4)])

19)   [9, 10, 11, 12, …, 74]

20)   [23, 24]

21)   [22]

Две Кучи решать руками сложнее, поэтому лучше написать программу.

№ 12737 (C. Горбачёв) (KompEge)

Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежат две кучи камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в одну из куч (по своему выбору) пять камней или увеличить количество камней в куче в два раза. Для того чтобы делать ходы, у каждого игрока есть неограниченное количество камней. Игра завершается в тот момент, когда произведение камней в кучах становится больше 384. Победителем считается игрок, сделавший последний ход, т.е. первым получивший такую позицию, при которой в кучах будет 385 или больше камней. В начальный момент в первой куче было восемь камней, во второй куче – S камней; 1 ≤ S ≤ 54. Будем говорить, что игрок имеет выигрышную стратегию, если он может выиграть при любых ходах противника.

Известно, что Ваня выиграл своим первым ходом после неудачного первого хода Пети. Укажите минимальное значение S, когда такая ситуация возможна. 

Задание 20.

Для игры, описанной в предыдущем задании, найдите минимальное и максимальное S, при которых у Пети есть выигрышная стратегия, причём одновременно выполняются два условия: 

− Петя не может выиграть за один ход;

− Петя может выиграть своим вторым ходом независимо от того, как будет ходить Ваня. 

В ответ запишите сначала минимальное значение, затем максимальное.

Задание 21.

Для игры, описанной в задании 19, найдите минимальное значение S, при котором одновременно выполняются два условия: 

–  у Вани есть выигрышная стратегия, позволяющая ему выиграть первым или вторым ходом при любой игре Пети;

–  у Вани нет стратегии, которая позволит ему гарантированно выиграть первым ходом.

19)    13

20)    10 19

21)    6

Решение: в условии сказано произведения куч обычно бывает сумма куч, поэтому условие нужно читать внимательно.

def f(x, y, m):     if x*y >= 385:

        return m % 2 == 0     if m == 0:         return 0     h = [f(x+5, y, m-1), f(x, y+5, m-1), f(x*2, y, m-1), f(x, y*2, m-1)]     return any(h) if (m-1) % 2 == 0 else all(h)

print('19)', [s for s in range(1, 55) if f(8, s, 2)]) print('20)', [s for s in range(1, 55) if not f(8, s, 1) and f(8, s, 3)]) print('21)', [s for s in range(1, 55) if not f(8, s, 2) and f(8, s, 4)])

Результат выполнения программы:

19)  [13, 14, 15, …, 54]

20)  [10, 11, 12, 13, 14, 15, 16, 17, 18, 19]

21)  [6, 7, 8, 9]

№ 11840 (Л. Шастин) (KompEge)

Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежат две кучи камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в одну из куч (по своему выбору) три камня или увеличить количество камней в куче в два раза. Для того чтобы делать ходы, у каждого игрока есть неограниченное количество камней. Игра завершается в тот момент, когда суммарное количество камней в кучах становится не менее 375. Победителем считается игрок, сделавший последний ход, т.е. первым получивший такую позицию, при которой в кучах будет 375 или больше камней. В начальный момент в первой куче было 27 камней, во второй куче – S камней; 1 ≤ S ≤ 347. Будем говорить, что игрок имеет выигрышную стратегию, если он может выиграть при любых ходах противника.

Известно, что Ваня выиграл своим первым ходом после неудачного первого хода Пети. Укажите минимальное значение S, когда такая ситуация возможна.

Задание 20.

Для игры, описанной в предыдущем задании, найдите наименьшее и наибольшее значения S, при которых у Пети есть выигрышная стратегия, причём одновременно выполняются два условия:

− Петя не может выиграть за один ход;

− Петя может выиграть своим вторым ходом независимо от того, как будет ходить Ваня. Найденные значения запишите в ответе в порядке возрастания.

Задание 21.

Для игры, описанной в задании 19, найдите минимальное значение S, при котором одновременно выполняются два условия:

–  у Вани есть выигрышная стратегия, позволяющая ему выиграть первым или вторым ходом при любой игре Пети;

–  у Вани нет стратегии, которая позволит ему гарантированно выиграть первым ходом.

19)  87

20)  159 172

21)  156

def f(x, y, m):     if x+y >= 375:

        return m % 2 == 0     if m == 0:         return 0     h = [f(x+3, y, m-1), f(x, y+3, m-1), f(x*2, y, m-1), f(x, y*2, m-1)]     return any(h) if (m-1) % 2 == 0 else all(h)

print('20)', [s for s in range(1, 375) if not f(27, s, 1) and f(27, s, 3)])

print('21)', [s for s in range(1, 375) if not f(27, s, 2) and f(27, s, 4)])

19)  83

20)  [159, 160, 170, 171, 172]

№ 27754 (Решу ЕГЭ)

Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежат две кучи камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в одну из куч один камень или увеличить количество камней в куче в четыре раза. Например, пусть в одной куче 6 камней, а в другой 9 камней; такую позицию мы будем обозначать (6, 9). За один ход из позиции (6, 9) можно получить любую из четырёх позиций: (7, 9), (24, 9), (6, 10), (6, 36). Чтобы делать ходы, у каждого игрока есть неограниченное количество камней.

Игра завершается в тот момент, когда суммарное количество камней в кучах становится не менее 61. Победителем считается игрок, сделавший последний ход, то есть первым получивший позицию, в которой в кучах будет 61 или больше камней.

В начальный момент в первой куче было 3 камня, во второй куче  — S камней, 1 ≤ S ≤ 57. Будем говорить, что игрок имеет выигрышную стратегию, если он может выиграть при любых ходах противника. Описать стратегию игрока  — значит, описать, какой ход он должен сделать в любой ситуации, которая ему может встретиться при различной игре противника. В описание выигрышной стратегии не следует включать ходы играющего по ней игрока, которые не являются для него безусловно выигрышными, то есть не гарантируют выигрыш независимо от игры противника.

Известно, что Ваня выиграл своим первым ходом после неудачного первого хода Пети. Укажите минимальное значение S, когда такая ситуация возможна. Задание 20.

Найдите два таких значения S, при которых у Пети есть выигрышная стратегия, причём одновременно выполняются два условия:

— Петя не может выиграть за один ход;

— Петя может выиграть своим вторым ходом независимо от того, как будет ходить Ваня.

Найденные значения запишите в ответе в порядке возрастания без разделительных знаков.

Задание 21.

Найдите минимальное значение S, при котором одновременно выполняются два условия: — у Вани есть выигрышная стратегия, позволяющая ему выиграть первым или вторым ходом при любой игре Пети;

— у Вани нет стратегии, которая позволит ему гарантированно выиграть первым ходом.

19)  4

20)  12 14

21)  13

def f(x, y, m):     if x+y >= 61:

        return m % 2 == 0     if m == 0:         return 0     h = [f(x+1, y, m-1), f(x, y+1, m-1), f(x*4, y, m-1), f(x, y*4, m-1)]     return any(h) if (m-1) % 2 == 0 else all(h)

print('20)', [s for s in range(1, 61) if not f(3, s, 1) and f(3, s, 3)])

print('21)', [s for s in range(1, 61) if not f(3, s, 2) and f(3, s, 4)])

19)  4

20)  [12, 14]

Шаблоны работают если задачи будут стандартного вида, то есть

19)  если Ваня выигрывает после хода Пети

20)  если Петя выигрывает после хода Ваня

21)  если Ваня выигрывает после хода Пети

Построение дерево в одной куче работает не всегда, большинство случаев да, работает, но для построение нужно понимать суть задачи, то есть Теории игр. Поэтому и для одной кучи, и для двух куч лучше написать программу.

Для лучшего понимания алгоритма написания программы:

https://www.youtube.com/watch?v=gLATLSQLqVg&t=5749s  

https://www.youtube.com/watch?v=Doa0fULDqn0&t=6317s  

https://www.youtube.com/watch?v=dYXdoI6nh9w&t=4161s