Поделиться
Разбор-27-задания.pdf
РАЗБОР 27 ЗАДАНИЯ
ЗАДАНИИ ВЗЯТЫ С САЙТА
https://kpolyakov.spb.ru/school/ege/gen.php?action=viewAllEgeNo&egeId=27&cat161=on&cat183=on _____________________________________________________________________________________
27) (№ 7581) (Демо-2025) Учёный решил провести кластеризацию некоторого множества звёзд по их расположению на карте звёздного неба. Кластер звёзд – это набор звёзд (точек) на графике. Каждая звезда обязательно принадлежит только одному из кластеров. Центр кластера, или центроид, – это одна из звёзд на графике, сумма расстояний от которой до всех остальных звёзд кластера минимальна. Расстояние между двумя точками A(x1, y1) и B(x2, y2) вычисляется по формуле:
Даны два входных файла (файл A и файл Б). В файле A
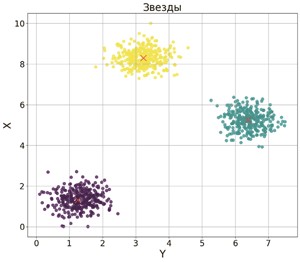
хранятся данные о звёздах двух кластеров. В каждой строке записана информация о расположении на карте одной звезды: сначала координата x, затем координата y (в условных единицах). Известно, что количество звёзд не превышает 1000. В файле Б хранятся данные о звёздах трёх кластеров. Известно, что количество звёзд не превышает 10 000. Структура хранения информации о звездах в файле Б аналогична файлу А. Возможные данные одного из файлов иллюстрированы графиком.
Для каждого файла определите координаты центра каждого кластера, затем вычислите два числа: Px – среднее арифметическое абсцисс центров кластеров, и Py – среднее арифметическое ординат центров кластеров. В ответе запишите четыре числа: в первой строке сначала целую часть произведения Px×10 000, затем целую часть произведения Py×10 000 для файла А, во второй строке – аналогичные данные для файла Б.
Решение
Если данные даны в текстовом документе, то есть формате .txt, то для анализа данных необходимо скопировать эти данные и вставить в электронную таблицу, то есть в EXCEL.
Испайханов Л. Л.
В текстовом формате
В формате EXCEL
Далее необходимо построить точечную диаграмму.
Для этого выделяем столбец А, столбец В > ВСТАВКА> ДИАГРАММЫ > ТОЧЕЧНАЯ
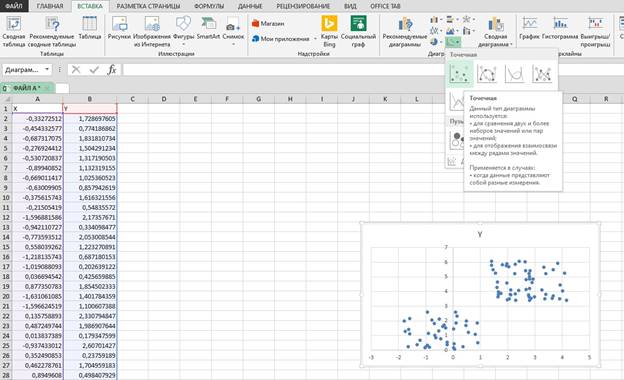
В файле А находиться два кластера, а в файле Б находиться три кластера как сказано в условии.
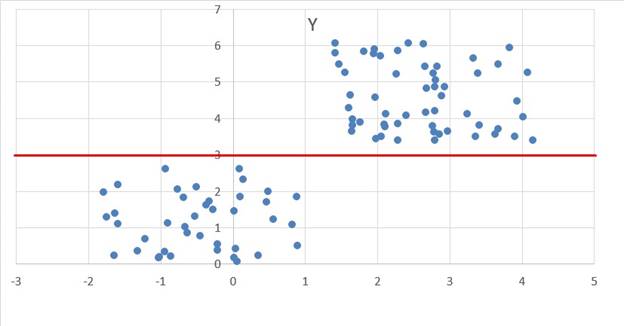
Визуально можем видит, что первый кластер находится ниже тройки по Y, а второй кластер выше тройки по Y.
Теперь после анализа данных можем перейти написанию кода.
Чтобы извлечь данные из файла, необходимо чтобы файл формате .py и файл в формате .txt были в одной папке или указать путь к файлу .txt.
|
# открываем файл file = open('27_A.txt') # пропускаем первую строку next(file) # создаем кластер 1 и кластер 2 в виде пустого списка klaster1, klaster2 = [], []
for line in file: # с помощью функции replace заменяем все запятые на точки # так как python считывает вещественные числа только с точкой # с помощью функции split разделяем точки х и у # с помощью функции map изменяем формат с строки на формат float x, y = map(float, line.replace(',', '.').split()) # если у < 3 то добавляем точки х и у klaster1 иначе klaster2 if y < 3: klaster1.append([x, y]) else: klaster2.append([x, y])
# создаем функцию dist как в условии def dist(x1, y1, x2, y2): return ((x2 - x1)**2 + (y2 - y1)**2)**0.5
# создаем функцию для нахождения центроида def centroid(klaster): # точки x_centr, y_centr центроида x_centr, y_centr = 0, 0 # минимальное расстояние центроида minim = 10**10
# помощью цикла перебираем все точки центроида то есть кластера |
|
for i in range(len(klaster)): # res промежуточный результат res = 0 for j in range(len(klaster)): # первая точка кластера x1, y1 = klaster[i] # вторая точка кластера x2, y2 = klaster[j] # находим промежуточный результат res += dist(x2, y2, x1, y1) # если промежуточный результат меньше минимального расстояния центроида if res < minim: # минимальному расстоянию центроида присваиваем промежуточный результат minim = res # точкам цетроида присваиваем первые точки минимального расстояния центроида x_centr, y_centr = x1, y1 # возвращаем точки цетроида return [x_centr, y_centr]
# для переменных x1, y1, x2, y2 с помощью функции centroid находим координаты(точки) # для перевого и второго кластера x1, y1 = centroid(klaster1) x2, y2 = centroid(klaster2) # находим среднее арифметическое этих точек px, py px = (x1 + x2) / 2 py = (y1 + y2) / 2 # выводим px, py умноженные на 10000 по условию print(px*10_000, py*10_000)
|
ТЕПЕРЬ ФАЙЛ Б
выделяем столбец А, столбец В > ВСТАВКА> ДИАГРАММЫ > ТОЧЕЧНАЯ
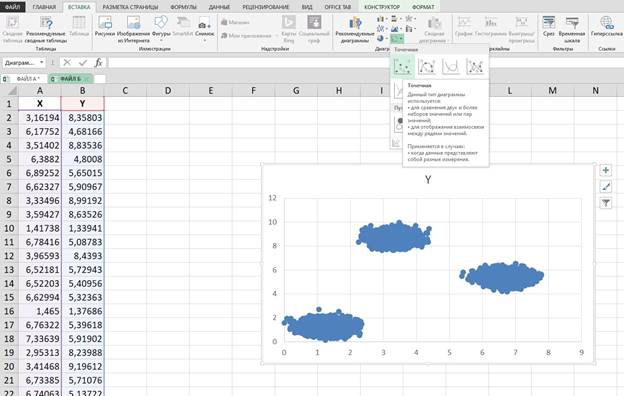
Нажав на ОСЬ У можем поменять формат оси для точного анализа меняем с двойки на единицу
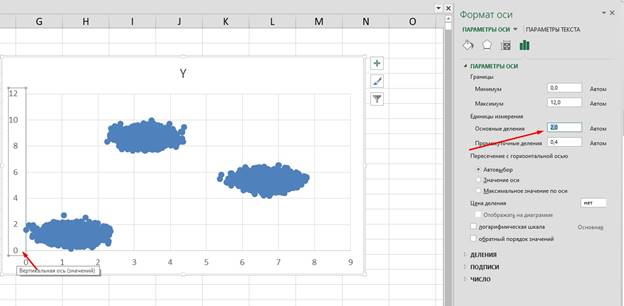
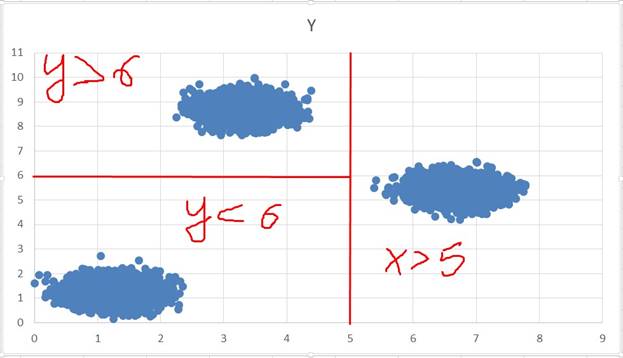
Визуально разделяем кластеры:
если по х больше 5, то это первый кластер иначе если по у больше 6, то это второй кластер иначе если по у меньше 6, то это третий кластер Для файла Б код изменяется незначительно:
1) Добавляется третий кластер
2) условия разделения на кластеры
3) добавляется х3, у3 для третьего кластера
4) рх и ру
|
10730 |
30730 |
|
37522 |
51277 |
ТО next(file) В КОДЕ НЕ ПИШЕТСЯ
|
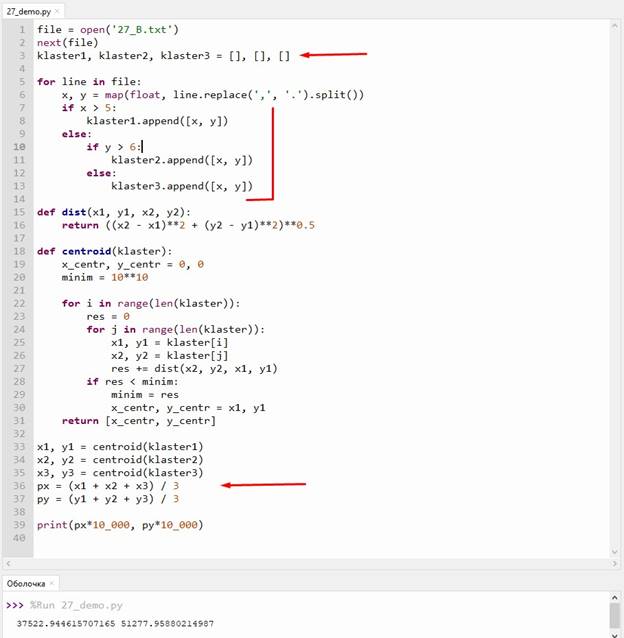
file = open('27_B.txt') next(file) klaster1, klaster2, klaster3 = [], [], []
for line in file: x, y = map(float, line.replace(',', '.').split()) if x > 5: |
|
klaster1.append([x, y]) else: if y > 6: klaster2.append([x, y]) else: klaster3.append([x, y])
def dist(x1, y1, x2, y2): return ((x2 - x1)**2 + (y2 - y1)**2)**0.5
def centroid(klaster): x_centr, y_centr = 0, 0 minim = 10**10
for i in range(len(klaster)): res = 0 for j in range(len(klaster)): x1, y1 = klaster[i] x2, y2 = klaster[j] res += dist(x2, y2, x1, y1) if res < minim: minim = res x_centr, y_centr = x1, y1 return [x_centr, y_centr]
x1, y1 = centroid(klaster1) x2, y2 = centroid(klaster2) x3, y3 = centroid(klaster3) px = (x1 + x2 + x3) / 3 py = (y1 + y2 + y3) / 3
print(px*10_000, py*10_000)
|
27) (№ 7583) Учёный решил провести кластеризацию некоторого множества звёзд по их расположению на карте звёздного неба. Кластер звёзд – это набор звёзд (точек) на графике. Каждая звезда обязательно принадлежит только одному из кластеров. Центр кластера, или центроид, – это одна из звёзд на графике, сумма расстояний от которой до всех остальных звёзд кластера минимальна. Расстояние между двумя точками A(x1, y1) и B(x2, y2) вычисляется по формуле:
Даны два входных файла (файл A и файл Б). В
файле A хранятся данные о звёздах двух кластеров. В каждой строке записана информация о расположении на карте одной звезды: сначала координата x, затем координата y (в условных единицах). Известно, что количество звёзд не превышает 1000. В файле Б хранятся данные о звёздах трёх кластеров. Известно, что количество звёзд не превышает 10 000. Структура хранения информации о звездах в файле Б аналогична файлу А. Возможные данные одного из файлов иллюстрированы графиком.
Для каждого файла определите координаты центра каждого кластера, затем вычислите два числа: Px – среднее арифметическое абсцисс центров кластеров, и Py – среднее арифметическое ординат центров кластеров. В ответе запишите четыре числа: в первой строке сначала целую часть произведения Px×10 000, затем целую часть произведения Py×10 000 для файла А, во второй строке – аналогичные данные для файла Б.
Решение
Файл А
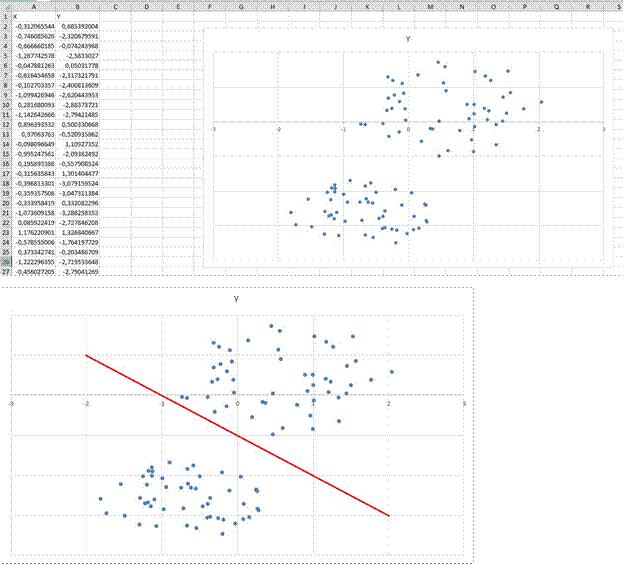
Как предыдущем задаче по х и по у определить кластеры не получиться. Чтобы определить рисуем прямую: y = kx + b
Находим прямую по формуле: (𝒚𝟏−𝒚𝟎)=𝒌(𝒙𝟏−𝒙𝟎)
При х = 0, b = -1 => y = kx – 1, возьмем точку (-1, 0)
0 = -1k - 1 => k = - 1 отсюда получаем уравнение: y = – x – 1 Тогда
если y > -x – 1, то это первый кластер иначе второй кластер
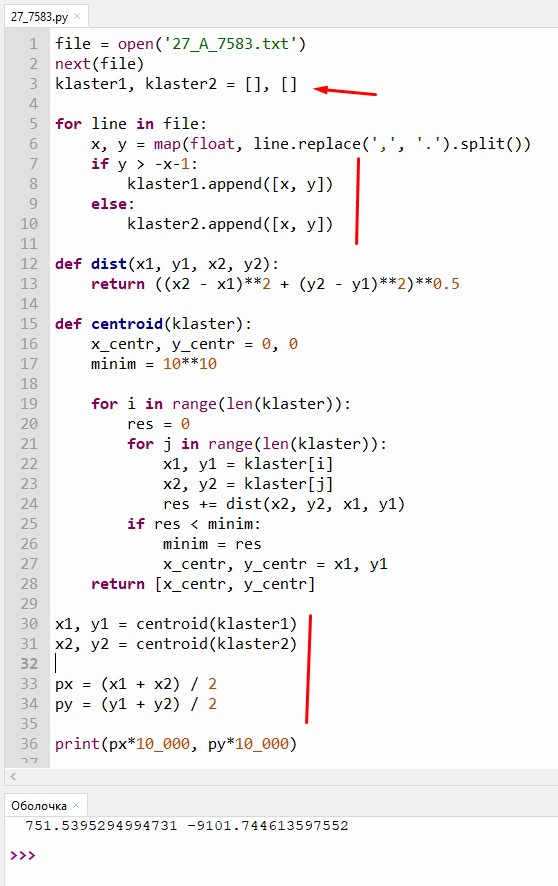
751 -9101
|
file = open('27_A_7583.txt') next(file) klaster1, klaster2 = [], []
for line in file: x, y = map(float, line.replace(',', '.').split()) if y > -x-1: klaster1.append([x, y]) else: klaster2.append([x, y])
def dist(x1, y1, x2, y2): return ((x2 - x1)**2 + (y2 - y1)**2)**0.5
def centroid(klaster): x_centr, y_centr = 0, 0 minim = 10**10
for i in range(len(klaster)): res = 0 for j in range(len(klaster)): x1, y1 = klaster[i] x2, y2 = klaster[j] res += dist(x2, y2, x1, y1) if res < minim: minim = res x_centr, y_centr = x1, y1 return [x_centr, y_centr]
x1, y1 = centroid(klaster1) x2, y2 = centroid(klaster2)
px = (x1 + x2) / 2 py = (y1 + y2) / 2 print(px*10_000, py*10_000)
|
Файл Б
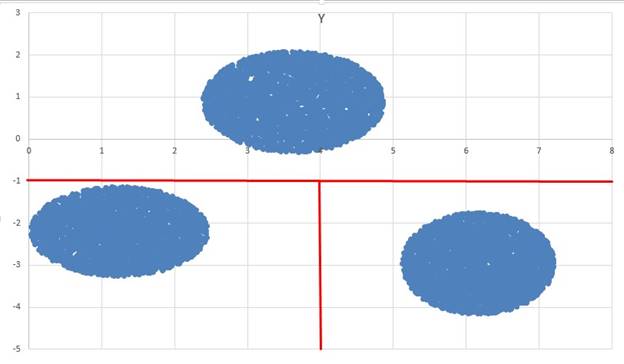
В файле Б находятся три кластера и можно разделить как показано на рисунке, но можно и через прямые
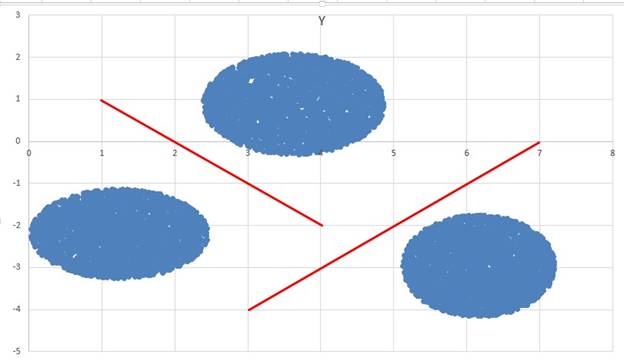
Первый вариант удобнее разделить кластеры, но можно и по второму варианту
Первый вариант:
Если у больше -1, то это первый кластер
Иначе если х меньше 4, то это второй кластер
Иначе если х больше 4, то это третий кластер
Если у меньше х – 7, то это первый кластер
Иначе если у больше – х+2, то это второй кластер
Иначе если у меньше – х+2, то это третий кластер
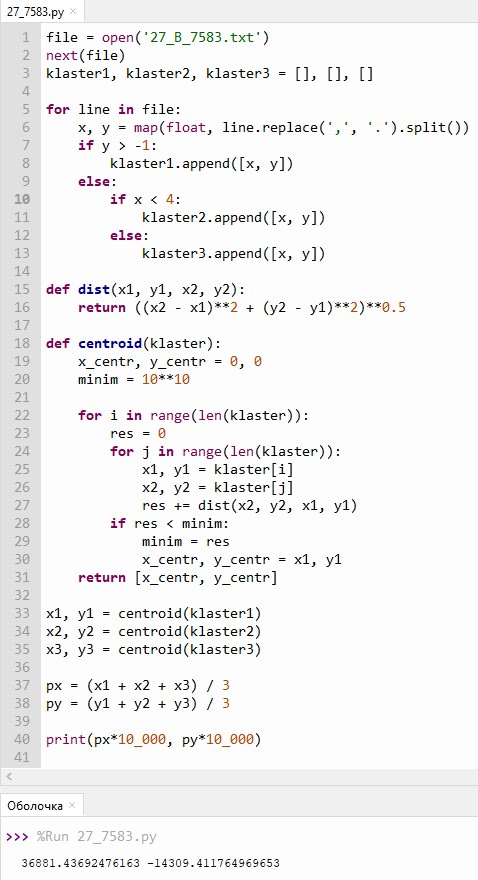
36881 -14309
|
file = open('27_B_7583.txt') next(file) klaster1, klaster2, klaster3 = [], [], [] for line in file: x, y = map(float, line.replace(',', '.').split()) if y > -1: klaster1.append([x, y]) else: if x < 4: klaster2.append([x, y]) else: klaster3.append([x, y])
def dist(x1, y1, x2, y2): return ((x2 - x1)**2 + (y2 - y1)**2)**0.5
def centroid(klaster): x_centr, y_centr = 0, 0 minim = 10**10 for i in range(len(klaster)): res = 0 for j in range(len(klaster)): x1, y1 = klaster[i] x2, y2 = klaster[j] res += dist(x2, y2, x1, y1) if res < minim: minim = res x_centr, y_centr = x1, y1 return [x_centr, y_centr]
x1, y1 = centroid(klaster1) x2, y2 = centroid(klaster2) x3, y3 = centroid(klaster3) px = (x1 + x2 + x3) / 3 py = (y1 + y2 + y3) / 3 print(px*10_000, py*10_000)
|
В ОТВЕТЕ ПРИШЕМ ТОЛЬКО ЦЕЛУЮ ЧАСТЬ:
|
751 |
-9101 |
|
36881 |
-14309 |
27) (№ 7644) (В. Шубинкин) В ходе эксперимента были зафиксированы очаги радиации. Чтобы изучить данное явление, решили провести кластеризацию источников излучения. Кластер – это набор источников (точек) на графике, лежащий внутри прямоугольника высотой H и шириной W. Каждая точка обязательно принадлежит только одному из кластеров. Истинный центр кластера, или центроид, – это одна из точек на графике, сумма расстояний от которой до всех остальных точек кластера минимальна. Расстояние между двумя точками A(x1, y1) и B(x2, y2) вычисляется по формуле:
Аномалиями назовём совокупности из не более
чем 10 точек, каждая из которых находится на расстоянии более одной условной единицы от точек кластеров. Аномалии в расчётах не учитываются. Даны два входных файла (файл A и файл Б). В файле A хранятся данные о точках двух кластеров. В каждой строке записана информация о расположении одной точки: сначала координата x, затем координата y (в условных единицах). Известно, что количество точек не превышает 1000. В файле Б той же структуры хранятся данные о трёх кластерах. Известно, что количество точек не превышает 10 000. Структура хранения информации о точках в файле Б аналогична файлу А. Возможные данные одного из файлов иллюстрированы графиком.
Для каждого файла определите координаты центра каждого кластера, затем вычислите два числа: Px – среднее арифметическое абсцисс центров кластеров, и Py – среднее арифметическое ординат центров кластеров. В ответе запишите четыре числа: в первой строке сначала целую часть произведения Px×100 000, затем целую часть произведения Py×100 000 для файла А, во второй строке – аналогичные данные для файла Б.
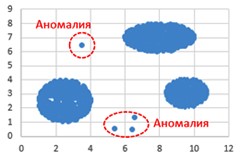
Решение
Файл А
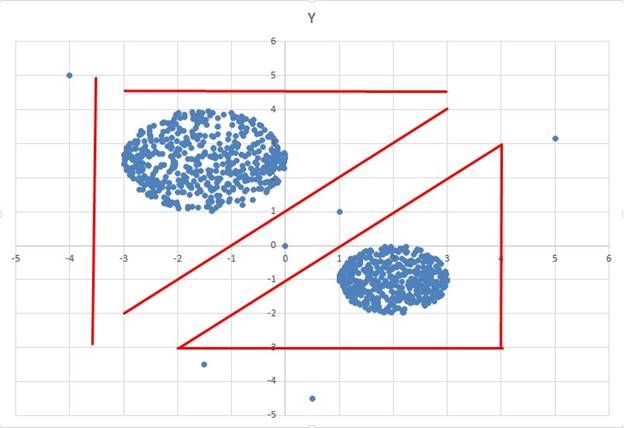
Если y > x+1 and y < 4,5 and x > -3,5, то это первый кластер
Иначе если y < x-1 and x < 4 and y > -3, то это второй кластер
АНОМАЛИИ НЕ ВХОДЯТЬ В КЛАСТЕРА
Ответ на файл А
19615 69089
ФАЙЛ Б
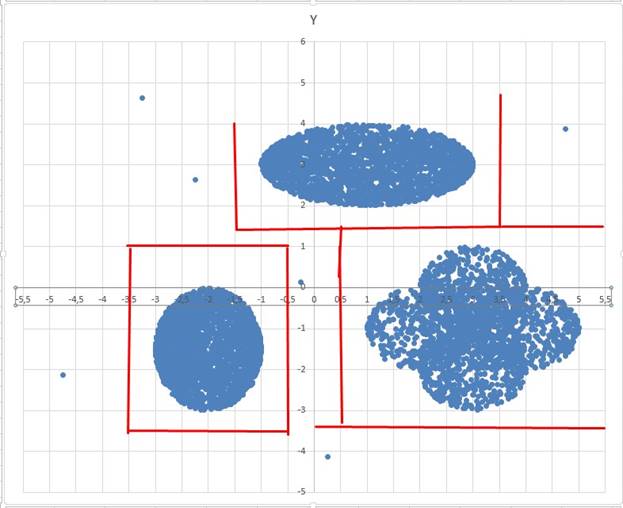
Если -3.5 < y < 1 and -3.5 < x < -0.5, то это первый кластер
Иначе если -3.5 < y < 1.5 and x > 0.5, то это второй кластер
Иначе если y > 1.5 and -1.5 < x < 3.5, то это третий кластер
Ответ на файл Б
67799 17717
Чтобы лучше понять разбор 27 задания рекомендую посмотреть видео
1) https://rutube.ru/video/cb3160dd13c74933be5a086d50d7171d/
2) https://www.youtube.com/watch?v=QHqUCVI80XE&t=23s 3) https://www.youtube.com/watch?v=jTytrUQT-Ew
4) https://www.youtube.com/watch?v=aJuVDirgEXg&t=2275s
![for i in range(len(klaster)): # res промежуточный результат res = 0 for j in range(len(klaster)): # первая точка кластера x1, y1 = klaster[i] # вторая…](https://fs.znanio.ru/d5af0e/2e/d7/ac6057a38792c9eae531a032fe93b2faad.jpg)
![A_7583.txt') next(file) klaster1, klaster2 = [], [] for line in file: x, y = map(float, line](https://fs.znanio.ru/d5af0e/4b/5b/048d8f8fc3a364e89cd8b1f5f5fdfc1fa2.jpg)
![B_7583.txt') next(file) klaster1, klaster2, klaster3 = [], [], [] for line in file: x, y = map(float, line](https://fs.znanio.ru/d5af0e/f9/a7/c56a355e46a27b0c0a7c05c731777eb786.jpg)
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.
