Разложение квадратного трехчлена_Методические рекомендации к уроку №2

Методические рекомендации к проведению урока

Тема урока: Разложение квадратного трехчлена

Тип урока: Урок изучения новой темы

Цели обучения:

8.2.1.2 выделять полный квадрат двучлена из трехчлена;

8.2.1.3 раскладывать квадратный трехчлен на множители;

Цели урока:

Учащиеся

ü выделяют полный квадрат двучлена из трехчлена;

ü раскладывают квадратный трехчлен на множители;

Структура урока

1.    Организационный момент. Целеполагание.

2.    Актуализация знаний и умений учащихся по пройденному материалу.

3.    Изучение нового материала.

4.    Решение задач.

5.    Подведение итогов урока. Рефлексия.

Теоретический материал к уроку, определения к понятиям и др.

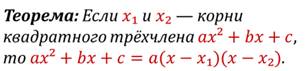
Замечание к теореме. Если дискриминант квадратного трехчлена ах²+bх+с  равен нулю, т.е. х₁=х₂ (кратный корень), то доказанная формула принимает вид:

Теорема. Если квадратный трёхчлен не имеет корней, то его нельзя разложить на множители, являющиеся многочленами первой степени.

Если у квадратного трехчлена существуют корни, тогда его можно разложить на множители.

Обратное тоже верно: если квадратный трехчлен можно разложить на множители, тогда у него есть корни.

Разложением квадратного трехчлена называется следующая ее запись:

ах² + bх + с = а(х – х₁)(х – х₂),

где х₁ , х₂ – корни квадратного трехчлена.

Инструкции к демонстрациям и технике безопасности.

Демонстрация материала осуществляется с помощью презентации PowerPoint. Слайды презентации содержат анимации, которые позволяют поэтапно вывести на экран решения и ответы к предложенным заданиям. Поэтому при показе презентации следует делать паузы после демонстрации заданий и постановки вопросов, давая учащимся время на их выполнение и обдумывание ответов.

Дополнительные методические рекомендации по организации урока.

Структура и организация урока нацелены на продуктивную деятельность учащихся при изучении новой темы, не допуская пассивного восприятия материала. В связи с этим учителю необходимо задавать учащимся вопросы высокого порядка, наталкивая их на «открытие» и освоение нового материала, при этом выдерживая паузы, необходимые для обдумывания.    

Дополнительные разноуровневые (на дифференциацию) задания.

Базовый уровень

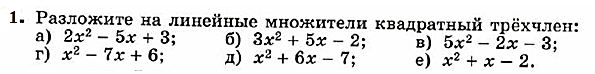
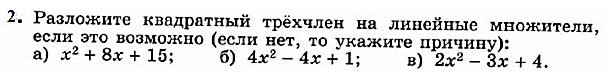
Продвинутый уровень

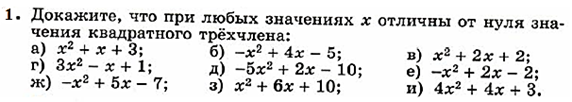
Рекомендации по формативному оцениванию.

Формативное оценивание производится на каждом этапе урока (самооценивание, оценивание учителем по критериям). Оценка путем наблюдения за вовлечением учеников в работу при выполнении заданий и за участием в диалогах. Прогресс, ответную реакцию на задания в парах, в группах необходимо отслеживать для того, чтобы оценить вклад каждого ученика и выявить наличие ошибок для их дальнейшей коррекции.

Ответы, критерии к заданиям, дополнительные материалы к уроку.

Ответы к заданиям содержатся в презентации урока и полезны для организации самооценивания или взаимооценивания учащихся.

Критерии оценивания к каждому заданию прописаны в приложениях к уроку, а также указаны в краткосрочном плане.

Список полезных ссылок и литературы.

Алгебра. 8-класс: Учебник для 8 класса общеобразовательной школы с русским языком обучения/ А.Н. Шыныбеков – 3-издание. – Алматы: «Атамұра», 2012. 288 с.

Алгебра. 8 класс : учеб. для учащихся общеобразоват. учреждений / Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, И. Е. Феоктистов. — 10-е изд., испр. — М. : Мнемозина,

2010.

https://interneturok.ru/lesson/algebra/8-klass/kvadratnye-uravneniya-prodolzhenie/razlozhenie-kvadratnogo-tryohchlena-na-mnozhiteli

http://lomonosovclub.com/ru/study_lists/34#!/articles/256

http://www.yaklass.ru/p/algebra/8-klass/kvadratnye-uravneniia-11021/teorema-vieta-9116/re-eee0a262-f7db-4e0b-87df-9079beb1b2ce

Скачано с www.znanio.ru