Разработка урока по теме "Решение треугольников"

“Геометрия является самым могущественным средством для изощрения наших умственных способностей и дает возможность правильно мыслить и рассуждать”.

                                                  Галилео Галилей

Тема урока:  «Решение треугольников»

Цели урока:

• систематизировать и обобщить знания учащихся по теме «Треугольники». Познакомить учащихся с методами решения треугольников, закрепить знание  теорем о сумме углов треугольника, синусов, косинусов, теоремы Пифагора, научить применять их в ходе решения задач.
• способствовать формированию умений применять приемы: сравнения, обобщения, выделения главного, переноса знаний в новую ситуацию, анализировать условие задачи, составлять модель решения.
• способствовать развитию умений и навыков применять математические знания к решению практических задач, ориентироваться в простейших геометрических конструкциях.

• содействовать воспитанию интереса к математике, активности.

Задачи урока:

1. Систематизировать полученные знания
2. Научить учащихся находить главное
3. Продолжить воспитание у учащихся уважительного отношения друг к другу.

Тип урока: урок изучения нового материала.

Форма урока: урок-поиск.

Оборудование: мультимедиапроектор,  таблицы Брадиса, таблицы-памятки для заполнения учащимися,  модели треугольников для исследований, чертёжные инструменты.

Ход урока

1. Организационный момент ( 2 мин)

 - Здравствуйте, ребята и наши уважаемые гости. Сегодня у нас пройдет открытый урок по геометрии по теме « Решение треугольников». На сегодняшнем уроке мы повторим материал, изученный вами на предыдущих уроках по теме «Соотношение между сторонами и углами треугольника», вспомним новую формулу нахождения площади треугольника, теоремы синуса и косинуса, узнаете, что значит «решить треугольник» и познакомитесь  с методами решения треугольников.

- Итак, тема нашего урока «Решение треугольников».

2. Обобщение и коррекция  опорных знаний по теме «Решение треугольников» (10 мин)

- Прежде чем мы приступим к изучению нового материала, немного повторим ранее изученное.

Теоретический опрос у доски: записать на доске определения синуса, косинуса, тангенса и котангенса острого угла прямоугольного треугольника, формулы площади треугольника, теорему Пифагора, формулы приведения, теорему синусов, косинусов(с целью обобщения и систематизации знаний и использования как опорно-наглядный материал в течение урока).

В это время с остальными учащимися проводится опрос с места на определение истинности  утверждения и правильности формулировок определений  ( подготовка к восприятию нового материала). Повторение некоторого теоретического материала по теме: «Треугольник» (Подготовка к ОГЭ)

1)        В треугольнике против угла в 150° лежит большая сторона. (И)

2)        В равностороннем треугольнике внутренние углы равны между собой и каждый равен 60°.(И)

3)        Существует треугольник со сторонами: 2 см, 7 см, 3 см. (Л)

4)        Прямоугольный равнобедренный треугольник имеет равные катеты. (И)

5)        Если один из углов при основании равнобедренного треугольника равен 50°, то угол, лежащий против основания, равен 90°.(Л)

6)        Если острый угол прямоугольного треугольника равен 60°, то прилежащий к нему катет равен половине гипотенузы. (И)

7)        В равностороннем треугольнике все высоты равны. (И)

8)        Сумма длин двух сторон любого треугольника меньше третьей стороны. (Л)

9)        Существует треугольник с двумя тупыми углами. (Л)

10)    В прямоугольном треугольнике сумма острых углов равна 90°.(И)

11)    Если сумма двух углов меньше 90°, то треугольник тупоугольный. (И)

12) По теореме косинусов можно определить вид треугольника.(И)

13) В треугольнике KLN,  KL=8,4 cм,  LN=13,2 см,  KN=7,5 см. Угол L треугольника наибольший. (Л)

14. Стороны треугольника 10см, 12см, 7см. Угол, противолежащий стороне 7см тупой.(Л)

Решение задач ОГЭ по готовым чертежам

1.      Найдите тангенс угла А треугольника АВС, изображенного на рисунке, размер клетки 1см х 1см

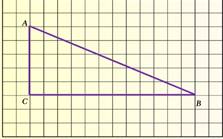
2.      Найдите синус угла А треугольника АВС, изображенного на клетчатой бумаге с размером клетки 1см х 1см

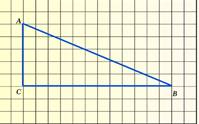
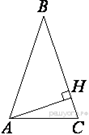
3.      В ост­ро­уголь­ном тре­уголь­ни­ке  вы­со­та  равна  а  сто­ро­на

  равна 40. Най­ди­те sin B.

         40

            20√3

4.      В треугольнике одна из сторон равна 10, другая равна , а угол между ними равен . Найдите площадь треугольника.

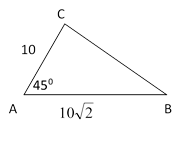
5.      Задан треугольник ABC, где AC=12, BC=10 и ∠ACB=60°. Найдите значение AB.

            В

                      10

                             60°  

           А        12             С

3. Изучение нового материала (15 мин)

- Во всяком треугольнике есть 6 основных элементов: 3 стороны и 3 угла. В теме “Решение треугольников” ставится вопрос о том, как, зная одни из основных элементов, найти другие.

 Решением треугольника называется нахождение всех его шести элементов (т. е. трех сторон и трех углов) по каким-нибудь трем данным элементам, определяющим треугольник.

Решение данных задач основано на использовании теорем синуса и косинуса, теоремы о сумме углов треугольника.

Причем, при вычислении углов треугольника предпочтительнее использовать теорему косинусов, а не теорему синусов.

Мы рассмотрим 4 задачи на решение треугольника (каждая группа получит свою задачу)

• решение треугольника по двум сторонам и углу между ними;
• решение треугольника по стороне и прилежащим к ней углам;
• решение треугольника по трем сторонам.
• Решение треугольника по двум сторонам и противолежащему к одной из них углу.

При этом будем пользоваться следующими обозначениями для сторон треугольника ABC: АВ = с, ВС =а, СА=b.

- У вас на столах лежат таблицы-памятки, которые к концу урока вы заполните.

Решение треугольника по двум сторонам и углу между ними	Решение треугольника по стороне и прилежащим к ней углам	Решение треугольника по трем сторонам	Решение треугольника по двум сторонам и противолежащему к одной из них углу.
			А   В                           С

Класс разбит на четыре группы. Каждый ученик группы под своим номером. ( Каждой группе выдаются модели геометрических фигур, инструменты, программы для решения задач, происходит коллективный разбор решения задачи).

Группа 1. Решить треугольник по двум сторонам и углу между ними

Группа 2. Решите треугольник по стороне и прилежащим к ней углам

Группа 3. Решить треугольник по трем сторонам.

В   А                             С	Дано: ∆АВС, а=6см, в=8см, А==30° Найти: АВ = с, В=С=	В    А                                   С Измерьте с помощью инструментов три элемента треугольника, вычислите остальные, проверьте свои вычисления.
1)По теореме синусов находим синус угла В;   Этому значению соответствуют два угла; °		1)
2) Если , то ° Если		2)
3) По теореме синусов находим третью сторону: Если  , , 4) Если  ,то		3)
Ответ:

Группа 4. Решить треугольник по двум сторонам и углу, прилежащему к одной из сторон

После данной работы, представитель от каждой группы составляет план решения задач своего типа. Остальные учащиеся записывают это в таблицу-памятку.

Решение треугольника по двум сторонам и углу между ними	Решение треугольника по стороне и прилежащим к ней углам	Решение треугольника по трем сторонам	Решение треугольника по двум сторонам и противолежащему к одной из них углу.
			А   В                           С
с = cos= = 180° - (+)	= 180° - (+) b= c=	cos= cos = = 180° - (+)

 Релаксация

Упражнение “Путешествие в волшебный лес“ 

  Звучит расслабляющая музыка.  

- “Представьте, что вы сейчас в лесу, где много деревьев, кустарников и всевозможных цветов. В самой чаще стоит белая каменная скамейка, присядем на неё.   Прислушайтесь к звукам. Вы слышите пение птиц, шорохи трав. Почувствуйте запахи: пахнет влажная земля, ветер доносит запах сосен. Запомните свои ощущения, чувства, захватите их с собой, возвращаясь из путешествия. Пусть они будут с вами весь день.”

4.         Закрепление изученного (10 мин)

Историческая справка:

Зачем нужны эти задачи? В Древней Греции, наряду с блестящим развитием теоретической геометрии, научных методов исследования и логических  доказательств, большое значение имела прикладная геометрия. Римляне вообще занимались лишь одной практической и прикладной стороной математики, необходимой для землемерия, строительства городов, технических и военных сооружений.

Нить практической геометрии тянулась от вавилонян и древних египтян через Герона вплоть до новых времён. 

В 16 – 17 веках всё более развивающаяся промышленность и торговля требуют удовлетворения, в первую очередь, практических нужд. Появление первых инструментов и аппаратов для научных исследований (термометра, телескопа, барометра, микроскопа и др.) вызвало интерес к практической стороне науки и особенно к практической геометрии, которая нужна была для военных целей, мореплавания, строительства и землемерия. В этот период появляется много руководств по геометрии, в которых излагаются правила, формулы и рецепты для решения тех или иных практических задач.

 Решение задач практического характера (количество решаемых задач зависит от оставшегося времени)

Задача № 1.   Пожарная лестница, стоящая на машине, может быть выдвинута на 20 м, а её крутизна может достигать 70⁰. Основание лестницы находится на высоте 2 м. До какого этажа можно по ней добраться, если высота этажа 3 м?

Задача № 2.   Спортивный самолёт летит по замкнутому треугольному маршруту. Два угла этого треугольника равны 60⁰ и 100⁰. Сторону, лежащую против третьего угла, он пролетел за 1 час. За сколько времени он пролетит весь маршрут, сохраняя постоянную скорость?

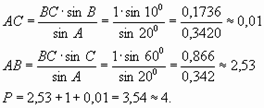
Ответ: за 4 часа самолёт пролетит весь маршрут.

Задача № 3.  Найдите длину отрезка, в концы которого упираются ножки циркуля-измерителя, длиной 15 см, если они образуют угол в 30⁰.

Дополнительная задача. Для украшения новогодней  елки высотой 6 м с двух противоположных сторон на расстоянии 4 м от елки вбили в землю два металлических полукольца. Какой должна быть длина тросов, протянутых от верхушки елки к полукольцам? Радиусом колец пренебречь. Найти угол наклона троса.

4.      Итоги (5 мин)

-Что значит решить треугольник? (Найти его неизвестные элементы по известным)

- Какое количество элементов должно быть известно, чтобы задача была решена? 

- Какие типы задач рассмотрели?

- Какие теоремы используются при решении  треугольников?

5.        Задание на дом ( на карточках) ( 1 мин)

          1) Задача.  «Две планки длиной 35см и 42см скреплены одним концом. Какой угол между ними надо взять, чтобы расстояние между другими концами планок равнялось 24см?»

2) №1025 (б, г)

3) параграф 103-104

6.      Рефлексия (2 мин)

Знания способны весь мир перевернуть.
Там, где есть желание, всегда найдётся путь!

– Перед вами правильный, прямоугольный и остроугольный треугольники. Если у вас на уроке все получалось правильно, то поднимите фигуру правильного треугольника, если остались от урока положительные эмоции, урок был интересным  – покажите прямоугольный треугольник, если в течение урока возникали проблемы – поднимите остроугольный треугольник.