Тема урока: «Ещё раз о функции второй степени…»
Ход урока
1. Организационный момент, формулировка темы и целей урока.
Учитель:
- Всё течет, все изменяется в окружающем нас мире, как заметили ещё древние. Вращается вокруг своей оси земной шар, и день сменяет ночь, Земля вершит свой вечный бег вокруг солнца, солнце вместе со всеми своими планетами вечно летит в космические дали. Кажется, причем здесь математика, а тем более функции и графики, о которых будем говорить. Но именно функция является тем средством математического языка, которое позволяет описывать процессы движения, изменения, присущие природе, а их графический образ – одно из важнейших средств выражения функциональной зависимости между величинами./Приложение1. Слайды 1-6 /
Ребята, о какой функции мы с вами говорили на последних уроках?
Учащиеся:
-О квадратичной функции.
Учитель:
- В каких случаях, при решении каких задач мы применяли данную функцию?
Учащиеся:
- Построение графика квадратичной функции и описание её свойств.
- Преобразования графиков квадратичных функций.
- Построение графиков кусочных функций.
- Применение квадратичной функции:
- при решении уравнений графическим способом,
- при решении систем уравнений графическим способом,
- при решении квадратных уравнений графическим способом,
- при решении неравенств графическим способом,
- при решении уравнений с параметром.
По мере того, как учащиеся отвечают, учитель составляет на доске кластер:
Учитель:
- Ребята, как вы думаете, всё ли уже вами усвоено по теме «Квадратичная функция»? Хотели бы вы узнать ещё что- то новое об этой функции, о её применении при решении практических задач?
Учащиеся рассуждают, отвечают.
Появляется кластер.
Учитель:
- Ребята, какая будет цель сегодняшнего урока?
Учащиеся:
- Совершенствовать знания, умения, навыки по теме «Квадратичная функция», рассмотреть применение квадратичной функции при решении практических задач.
Учитель:
- Ребята, сегодняшний урок я назвала «Ещё раз о функции второй степени…», а эпиграф к уроку - слова А. Франса: «Вы ведь не математик? Нет. Ну, так с вами и
спорить нечего, я спорю только с теми, кто владеет методами математического анализа».
На сегодняшнем уроке мы продолжим с вами учиться рассуждать, анализировать, сравнивать и открывать новые знания, применять эти знания при решении практических задач. Но прежде чем говорить об использовании квадратичной функции при решении практических задач, проверим наши теоретические знания.
2. Актуализация усвоенных знаний учащихся.
Учащийся представляет проект «Моя контрольная работа по теме «Квадратичная функция»».
Задание №1. На рисунке 1 изображены графики квадратичных функций. Заполнить таблицу.
|
№ |
вопросы |
номер графика |
|
1 |
График какой квадратичной функции указывает на то, что функция на всей области определения принимает только положительные значения. |
|
|
2 |
Какой из графиков указывает на отсутствие нулей функции?
|
|
|
3 |
Какой из графиков указывает на то, что функция имеет только один нуль? |
|
|
4 |
Какой из графиков указывает на то, что нули функции имеют разные знаки? |
|
|
5 |
Для какого графика верно, что функция возрастает при х≥ -1?
|
|
|
6 |
Для какого графика верно, что функция принимает отрицательные значения при х< -4, х >-2? |
|
|
7 |
Для какого графика верно, что ось симметрии графика является прямая х=4? |
|
|
8 |
Для какого графика верно, что наименьшее значение функции равно -4? |
|
|
9 |
Для какого графика верно, что наибольшее значение функции достигается при х= -3? |
|
|
10 |
Для какого графика верно, что f(0) = -3? |
|
После выполнения задания взаимопроверка в парах. Правильные ответы – на интерактивной доске.
Задание №2. Рассмотрите четыре функции, представленные аналитически или графически.
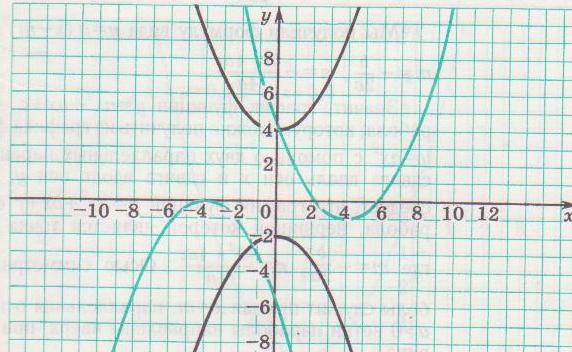
Для каждого графика укажите соответствующую формулу.
а) у=-1/3(х+4)2
б) у= 1/3 (х-4)2 -1
в) у=1/3х2 +4
г) у=-1/3х2 – 2
После выполнения задания взаимопроверка в парах. Правильные ответы – на интерактивной доске.
Обсуждение результатов выполненных заданий.
Задание №3 учащийся оформляет на интерактивной доске.
Задания №4, №5 двое учащихся выполняют у доски, остальные – в тетрадях.
Задание №3. На рисунке 2 изображены графики функций у=х2 -2х-3, у= -2х+1, у= -5. Используя графики квадратичной и линейных функций, решите уравнения, системы уравнений, неравенства.
|
№ |
задания |
варианты ответов |
верный ответ |
|
1 |
Используя график квадратичной функции, решите уравнение: х2 -2х-3=0. |
а) х1=-1, х2=3 б) х1=-4 в) х1=-1 г) нет верного ответа |
|
|
2 |
Используя графики квадратичной и линейной функций, решите уравнение: х2 -2х-3=-2х+1 |
а) х1=-1, х2=3 б) х1=-2, х2=2 в) х1=-1 г) нет верного ответа |
|
|
3 |
Используя графики, решите систему уравнений:
у=- 2х+1.
|
а) (0;-3) б) (-2;5), (2;-3) в) (-2;5), г)нет верного ответа |
|
|
4 |
Используя графики, укажите, сколько решений имеет система уравнений:
у= -5 |
а) 1 б) нет решений в) 2 г)нет верного ответа |
|
|
5
|
Используя график квадратичной функции, решите неравенство: х2- 2х- 3 >0. |
а) -1< х<3 б) х≥ 3 в) х< -1, х>3 г)нет верного ответа |
|
|
6 |
Используя графики квадратичной и линейной функций, решите неравенство: х2 -2х-3>-2х+1.
|
а) х<-2, х>2 б) -2< х<2 в) х>2 г)нет верного ответа |
|
|
7 |
При каких значениях р уравнение х2 -2х-3=р имеет один корень? |
а)р=-1 б)р=-4 в)р=-1, р=3 г)нет верного ответа |
|
Задание №4. Выясните, сколько корней имеют уравнения:2х2+5х+5=0, 2х2-5х-3=0.
Задание №5. Постройте график функции у=f (х), где
(1-х) (х+3), если х≤ 1,
f (х) =
(х-1) (х+3), если х>1.
При каких значениях m прямая у = m имеет с графиком этой функции две общие точки?
Подводятся итоги выполненных заданий.
Итоги подводит учащийся, выполнявший проект «Моя контрольная работа по теме «Квадратичная функция»». Оценивает учащихся.
Учитель:
-Ребята, как вы оцениваете проект «Моя контрольная работа по теме «Квадратичная функция»»?
Какие задания показались вам наиболее интересными? Какие задания вызвали у вас трудности?
Обсуждение учащихся.
3.Применение теоретических основ при решении практических задач.
/Приложение1. Слайды 10-14 /
Учитель:
- Зримая форма квадратичной функции проста, красива … и встречается на каждом шагу. Наблюдая за игрой в волейбол, можно увидеть, что траектория полета мяча имеет форму параболы.
Останавливаясь у фонтана и всматриваясь в каскад водяных брызг, разглядывая струи – одну, потом две, потом все вместе, рисуется тот же графический образ.
Представление о параболе даёт траектория тела, брошенного под углом к горизонту (из-за сопротивления воздуха эта траектория несколько отличается от параболы).
В темной комнате на столе стоит горящая свеча, над ней помещено кольцо. Тень от этого кольца так же отбрасывает кривую – параболу.
В технике используются параболические рефлекторы. Лучи от источника, помещенного в фокусе F, отражаются параллельно оси симметрии параболы. Квадратичная функция используется и при описании некоторых физических процессов.
Учащийся представляет проект «Функция, скрывающаяся за движением тел». /Приложение №4,5/
Обсуждение проекта.
Задания на применение квадратичной функции при решении практических задач./Приложение 4.Слайды 15-17/
1.Мяч подбросили вертикально вверх, и он упал на землю. На рисунке изображен график зависимости высоты мяча над землей от времени полета. Используя график, выясните, сколько метров пролетел мяч за первые 3 секунды. Через сколько секунд после броска мяч был на высоте, равной 6 метров?
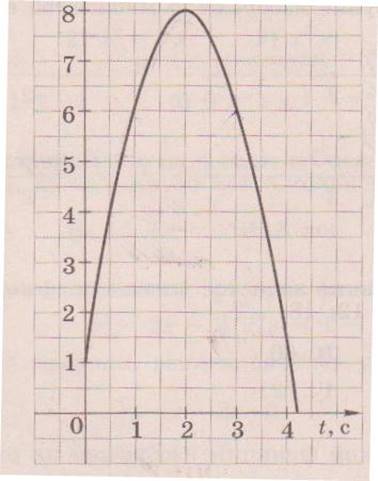
2. Движение дельфина, выпрыгивающего из воды вертикально вверх, описывается формулой
у= t -5t2. График функции изображен на рисунке.
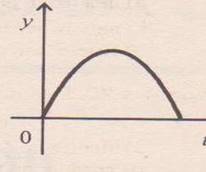
Объясните, что физически означают:
а) нули функции;
б) интервалы возрастания (убывания) функции;
в) наибольшее значение функции.
3. Дельфин выпрыгивает из воды вертикально вверх со скоростью v0=10 v/c. Через сколько секунд он упадет в воду?
Работа в группах. Обсуждение задач.
5.Подведение итогов. Рефлексия.
Учитель:
- Я снова хочу обратиться к словам А.Франса «Вы ведь не математик? Нет. Ну, так с вами и спорить нечего, я спорю только с теми, кто владеет методами математического анализа».
Ребята, что нового вы узнали сегодня на уроке? Мог ли с вами поспорить А.Франс? Вступил бы он с вами в диалог?
Достигнута ли вами цель сегодняшнего урока?
Учитель закрывает знак вопроса в кластере словами: «Использование квадратичной функции при описании свободного падения тел».
6.Домашнее задание.
Выполнить задания №6,№7 из проекта «Моя контрольная работа по теме «Квадратичная функция»».
Тема урока: «Ещё раз о функции второй степени…»
Учитель: - Ребята, как вы думаете, всё ли уже вами усвоено по теме «Квадратичная функция»?
Учитель: - Ребята, какая будет цель сегодняшнего урока?
Актуализация усвоенных знаний учащихся
Для каждого графика укажите соответствующую формулу
Используя графики, решите систему уравнений: у=х 2 -2х-3, у=- 2х+1
Останавливаясь у фонтана и всматриваясь в каскад водяных брызг, разглядывая струи – одну, потом две, потом все вместе, рисуется тот же графический образ
Движение дельфина, выпрыгивающего из воды вертикально вверх, описывается формулой у= t -5 t 2
Разработка урока "Ещё раз о функции второй степени..."
© ООО «Знанио»
С вами с 2009 года.
