Развитие творческих способностей учащихся при решении проблемных задач по геометрии

Развитие творческих способностей учащихся при решении проблемных задач по геометрии

Каждый, кто стремился создавать в учебном процессе проблемные ситуации и занимался поисками различных способов решения задач, должен обратить внимание на то, что в названных видах учебной работы много общего. Прежде всего, они оба способствуют повышению эффективности обучения, так как в основе каждого из них лежит активный мыслительный процесс. Далее, как и в проблемной ситуации, так и при решении задач различными способами наиболее полно проявляется взаимосвязь знаний и действий. Проблемная ситуация может возникнуть в ходе анализа задачи и, в свою очередь, послужить стимулом для поиска различных способов ее решения. Польза такой работы связана еще и с тем, что с пополнением знаний у учащихся расширяется круг вопросов, которые они могут применить к решению проблемной задачи

Рассмотрим примеры такой творческой деятельности на примере разбора одной задачи.

1. Через данную точку А проведите прямую, проходящую через лежащую вне чертежа точку пересечения данных прямых а и в.

После изучения свойств параллелограмма учащимся была предложена задача: «Имеются две непараллельные прямые а и в и отмечена точка А. Поднимите руки те, кто сможет провести прямую через отмеченную точку А и точку пересечения прямых а и в.

Руки подняли почти все учащиеся. Но спустя минуту, когда на доске появился рис. 1, учащиеся руки опустили. 

Рис. 1

Они не знали, как выполнить поставленное требование. 

Мною было отмечено, что данная задача имеет практическое значение.

Создалась проблемная ситуация. Учащиеся с интересом принялись за поиски решения.

Различные подходы обсуждались всем классом.

Вскоре появился первый способ решения: проведем прямые АС || а и АВ || в (рис. 2).

Прямая, соединяющая точку А с серединой отрезка ВС (точкой О), искомая.   

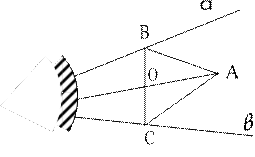
Рис. 2

Одобрив это решение, я сделала новый чертеж так, что прямые, проведенные через точку А и параллельные пересекают данные прямые а и в в недоступных точках (рис. 3).

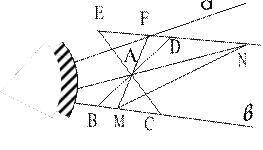
Рис. 3

Возникла проблемная ситуация. Учащиеся увидели, что приведенный выше способ применим не всегда. Возникшее затруднение вызвало необходимость устранения «преграды».

Теперь для решения задачи потребовалось воспользоваться центральной симметрией.

Пусть Вв и Св (рис. 3), Z_А(В)=D, а Z_A(C)=E, тогда DE||в. Если F=DEI a, а  M=AFI в, то

ZA(F)=M, то есть AF=AM. Проведя прямую MN, параллельную прямой а, и обозначив N=MNI DE, убеждаемся, что NA – искомая прямая.

Далее, чтобы натолкнуть учащихся на идею применения других геометрических свойств, было предъявлено требование использовать для построения только угольник с прямым углом. Возникла новая проблема. Снова поиски, и опять решение: АВ  в, АС а (рис. 4), D=a AB, E=вАС и AF DE; прямая AF – искомая (рис. 4).

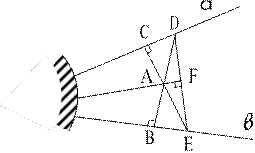
Рис. 4

Работа над задачей была продолжена на внеклассных занятиях. Учащимся был дан совет воспользоваться аналогией с только что описанным способом. Здесь решение задачи основывается на том, что высоты треугольника пересекаются в одной точке. Но можно применить и аналогичное свойство медиан. И снова затруднения, новая ситуация. Учащимся была предоставлена возможность думать над задачей дома. В результате появился четвертый способ решения задачи. Он сводился к последовательным построениям: АВ || в, АС || а, ВD=AC (рис. 5), Е = вI AD, O=BEI CDC, AO – искомая прямая (рис. 5).

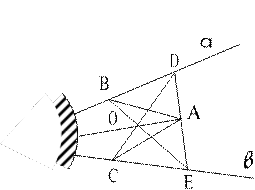
Рис. 5  

Действительно, пусть F =aIв , тогда АВFC – параллелограмм и АС = ВF. А так как АС =

ВD (по построению), то В – середина отрезка DF. Учитывая, что АС || а, АВ || в, заключаем: точки В, С, А – середины сторон треугольника FDE, а ВЕ, DC, AF – его медианы.

Рассмотренный пример длительной работы учащихся над одной задачей в школе почти не практикуется. Между тем творчество почти немыслимо без долгого раздумья над проблемой. Заботясь о развитии творческих способностей учащихся, мы должны создавать в учебном процессе такие ситуации, при которых дети длительное время думают над отдельными задачами. Польза такой работы связана еще и с тем, что с пополнением знаний у учащихся расширяется круг вопросов, которые они могут применить к решению проблемной задачи. Таким образом, богатый учебный материал осмысливается в разнообразных ситуациях, а не в виде изолированных кусков.