Развитие логического мышления при изучении умножения и деления. Выступление на ГМО.

Развитие логического мышления при изучении умножения и деления

Изучение умножения и деления является основой курса математики для 2-го класса. Занковская методика изучения этих действий строится так, чтобы овладение ими было сосредоточено вокруг определѐнных вопросов: связи умножения со сложением, переместительного и распределительного закона умножения, связи между умножением и делением. 

Понимание связи между сложением и умножением существенно помогает построить систему знаний, вытекающих друг из друга, а также овладеть различными способами нахождения значения произведений. Знание переместительного закона умножения значительно  сокращает количество случаев умножения, которые нужно запоминать. Понимание связи между умножением и делением даѐт возможность каждый случай умножения связать с соответствующими случаями деления. Это делает ненужным специальное запоминание случаев табличного деления. Основные положения об изучении сложения и вычитания, изложенные в соответствующем разделе методических рекомендаций для первого класса, сохраняются и для темы «умножение и деление».

Действие умножение вводится как особый случай сложения – сложения одинаковых чисел. Начало работы лучше связать с заданиями, в которых используются группы реальных предметов или их изображений.

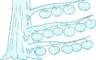1.Рассмотри рисунок: - Что ты можешь сказать о количестве яблок на ветках? 

-                     Как узнать, сколько яблок на всех ветках вместе?  Запиши действие.  (4+5+6).

2.Рассмотри рисунок: 

-                     Что можно сказать о количестве яблок на этих ветках?

-                     Сколько всего яблок на этих ветках? Запиши действие. (5+5+5).

-                     Сравни записанные выражения. Чем они похожи? Чем отличаются? 

Запиши ещѐ две суммы, похожие на первую сумму, и две, похожие на вторую. 

Сравнение выражений, соответствующих предложенным ситуациям, подведѐт детей к осознанию особенности суммы, состоящей из одинаковых слагаемых. Затем можно перейти к оперированию только суммами, состоящими из равных или неравных слагаемых. Результатом проводимых наблюдений является выделение сумм с одинаковыми слагаемыми в особую группу.

Умение выделять такие суммы можно считать основанием для перехода к изучению умножения. Установить этот момент помогут задания на классификацию. Например: на какие две группы можно разделить все эти суммы? Запишите каждую группу в отдельный столбик.

      7+9+5                                 4+14+24+44                             6+6

      19+19+19                           12+15+10

      7+7+7+7+7                          54+45

Таким образом, первый этап изучения новой темы включает знакомство с особыми суммами, их выделение в особую группу, введение определения действия умножения, формы записи этого действия. Дети узнают названия компонентов умножения, результаты  выполненного действия. Овладевают умением заменять сложение умножением и выполнять обратную операцию.

Деление рассматривается как действие обратное умножению, когда по известному значению произведения и одному множителю нужно найти второй множитель. Общее направление работы с этим действием аналогично приѐмам работы с вычитанием. Дальнейшее изучение темы включает два основных вопроса: изучение табличного умножения и деления и изучение умножения и деления двузначных и трѐхзначных чисел на однозначное число (внетабличное умножение и деление). Табличное умножение и деление.

Составление таблицы умножения начинается с выделения из таблицы сложения сумм с одинаковыми слагаемыми. Таким образом, в отличие от общепринятого подхода к началу составления таблицы умножения, когда число 2 умножается на все однозначные числа, в данном случае дети знакомятся в первую очередь с умножением всех однозначных чисел на 2. Такой подход к составлению таблицы принципиально важен, так как он способствует осуществлению одного из основных положений системы – активному использованию ранее приобретѐнных детьми знаний при изучении нового материала, а также углубляет понимание связи между действиями. Так же как при составлении таблицы сложения, в работе по составлению таблицы умножения можно выделить несколько этапов:

-            первый этап заключается в преобразованиях предложенных в заданиях выражений: последовательно составляются отдельные столбики таблицы умножения. Параллельно с этой работой дети знакомятся с переместительным законом умножения;

-            на основании переместительного закона умножения дети выполняют сокращение составленной части таблицы до необходимого минимума;

-            третий этап заключается в дальнейшем составлении таблицы умножения с использованием уже накопленного опыта, т. е. сокращение таблицы происходит при составлении каждого отдельного столбика. В таблицу вносятся только те строчки, необходимые для заучивания. Полученная краткая таблица записывается на отдельный листок, наклеивается на картон и используется в качестве справочного материала.

Параллельно с изучением умножения вводится и действие деления. Уже с первых шагов дети должны воспринимать деление как действие, связанное с умножением обратной зависимостью.

Этому способствует рассмотрение их на одном и том же материале. Такой вариант представлен в задании, где дети сначала получают отрезок одинаковой длины, а затем выполняют обратную операцию.  Начерти отрезок 6 см. Начерти сумму двух таких отрезков. Запиши сумму числами. Каким ещѐ действием можно найти сумму? – 4 см и т. д.

      6+6=12                                                       6 · 2=12

      4+4+4=12                                                    4 · 3=12

      3+3+3+3=12                                                3 · 4=12

      2+2+2+2+2+2=12                                        2 · 6=12

      1+1+1+1+1+1+1+1+1+1+1+1=12                1 · 12=12

- Начерти отрезок 12 см. Раздели его пополам. И т. д.

Знакомя учащихся с действием деления, мы стараемся представить его с разных точек зрения: рассматривать случаи деления на равные части, деления по содержанию, кратное сравнение чисел. Осознание связи между умножением и делением даѐт возможность значительно разгрузить память детей, избавив их от специального запоминания результатов деления в пределах таблицы умножения.

Так же как и при изучении сложения и вычитания большое значение для осознания взаимосвязи между умножением и делением имеет решение простейших уравнений (а · х = в, х · а

= в, а : х = в, а : а = в).

Внетабличное умножение и деление на однозначное число.

Расположение материала в программе 2 класса позволяет изучать эту тему одновременно на множестве и 2-значных и 3-значных чисел. Используется возможность выполнения действия не со всем числом в целом, а с отдельными его частями (т. е. замена числа суммой нескольких слагаемых на основе таблицы умножения).

На примере выполнения умножения круглых десятков и сотен на однозначные числа начинает формироваться понимание использования таблицы умножения для получения значения произведений внетабличных случаев. Объединение этих двух линий работы  даѐт выход к знакомству с умножением любых чисел на однозначное число. На этом этапе дети начинают выполнять умножение не более чем однозначных чисел на 3-значные. Однако можно попытаться предложить ученикам выполнить умножение на однозначное число и чисел, имеющих большее число разрядов. Такой выход за пределы изученного множества чисел является наиболее эффективным способом установления осознанности и глубины понимания изученного материала. На первом этапе изучения, как умножения, так и деления на однозначное число дети обязательно выполняют подробную запись: 

147 · 3 = (100+40+7) ·3 = 100 · 3 + 40 · 3 + 7 · 3 = 300+120+21 = 441

Только тогда, когда такая запись будет выполняться вполне сознательно всеми учащимися класса, учитель знакомит их с записью в столбик.

При изучении умножения не следует выстраивать различные случаи по трудности. Лучше использовать другой принцип построения материала: разобрать общие подходы к выполнению действий без дифференцирования по степени трудности  предлагаемых произведений, а затем проводить сравнение различных частных случаев для выявления степени их сложности.

(Например, случаи без перехода через разряд и с переходом; с одним переходом через разряд и с 2 переходами; с нулями в многозначном множителе и без нулей и т. д.).

     Изучение деления строится в той же логике, что и умножение. Однако здесь важно выделить ещѐ одну дополнительную линию наблюдения за процессом выполнения действий: случаи выделения в делимом разрядных  и удобных слагаемых. 

     Среди большого количества учебников математики для начальных классов выбор, к сожалению, не всегда делается в пользу «развивающих» учебников. Упрѐки по отношению к «развивающим» учебникам, в основном, сводятся к тому, что эти учебники содержат недостаточное  количество упражнений, направленных на формирование вычислительных навыков. Говоря об этом, большинство учителей сетует на отсутствие «столбиков примеров», обычно рассматриваемых как определѐнный вид заданий, в процессе выполнения которых у детей формируются вычислительные навыки.                                    

     Формирование прочных навыков в условиях развивающего обучения имеет свои особенности, которые надо учитывать при анализе «развивающих» учебников и в процессе подготовки и проведения уроков по ним. Среди этих особенностей можно назвать нацеленность на формирование обобщѐнных способов действий, самостоятельный поиск новых способов действий и отказ от однообразных тренировочных упражнений. Однообразная деятельность тормозит познавательную активность. Выполнение однотипных упражнений, конечно, способствует усвоению алгоритма вычислительного приѐма, но имеет и отрицательный эффект. Познавательная активность в этом случае высока лишь в момент ознакомления с новым способом, далее она постепенно снижается: пропадает интерес, рассеивается внимание, нарастает число ошибок. Предлагаю систему таких упражнений данной темы.

1. Выбери те выражения, в которых многозначное число умножается на однозначное:

            2 · 3                 203 · 3             213 · 1             23 · 10             2130 · 3

            23 · 3               2345 · 2            213 · 0             23 · 11              213 · 9

            213 · 3             3 · 2543            29 · 9               213 · 10            213 · 6 

- Значения каких выражений ты можешь найти? - Замени, где можно, умножение сложением и найди значение выражений. (Некоторые учащиеся могут решить большинство выражений, используя замену произведения суммой, опираясь на распределительное свойство умножения, правило умножения числа на 0, 1, 10). После этого предлагается следующее задание.         

2.  Сравни записи: 

3.  Объясни, как выполнено умножение:

 321 203 234 234 7981 2056     80409 5002      8567          55555  х  2 х  3 х  4 х  7 х    8 х    4     х      3 х    6      х    9          х     5  642 609 936     1638     63848 8224   241227          30012    77103       277775      Особенности записи компонентов «в столбик» при умножении и сложении рассматривается в задании 4.

4.  Чем похожи и чем отличаются записи? Все ли записи выполнены верно?

                          213

 213       +213    213     213       213             213     210  х  3   213    х   3     х  3         х  6           х  6           х  6            639   639    216     243       1278           1278         1260

5.  Выполни умножение «в столбик»:

            Это задание позволяет не только  совершенствовать вычислительные умения, но и содержит дополнительное указание сравнить значения некоторых выражений. При этом одни учащиеся будут из большого результата вычитать меньший, а другие, опираясь на смысл действия умножения, дадут ответ без вычислений. Отличительной особенностью этого и следующих заданий является то, что каждое из этих заданий дополняется различными вопросами, которые активизируют мыслительную деятельность учащихся и устанавливают связь между содержательным аспектом обучения и формированием вычислительных умений.

6.  Вставь цифры в «окошки» так, чтобы запись была верной:  

            6082                 2030□              147306             69□47              701□ 

            х    7                 х      4               х        □             х      □              х    4

          42□7□                 8□□28              5□92□4           4□5429            280□4

Для каждого выражения есть два способа постановки цифр. Найди оба способа. (Это важно для последнего столбика. Последней цифрой 1-го множителя может быть 1 или 6).

7.Найди значение выражений:

            387 · 2              596 · 4             789 · 3             1298 · 5           7657 · 4

Догадайся, как, используя полученные результаты, найти значения следующих выражений, не выполняя действия умножения:

            387 · 4              596 · 3             789 · 9              1298 · 10         7657 · 6

            387 · 6              596 · 2             789 · 6              1298 · 15         7657 · 2

Проверь результаты с помощью действия умножения. 

(789 · 3 + 789 · 3 или  789 · 9 - 789 · 3;  7657 · 6 - 7657 · 4 или 7657 · 4 – 7657 – 7657) 8.Найди ошибки в вычислениях:

8594                40567      8004              6387  5009     х    5                 х    8       х        9             х      4               х    9

          40550                 325536                 7236                2548            45881

8352                  2003      2345            84395    978     х    7                 х      9  х        3          х    7                 х    8

          58464                 18007      9255            589765              7374 9.Вычисли:

            1023 · 2           2013 · 2           Сравни столбики. Что у них общего? Составь такой же столбик,     1032 · 2          2031 · 2           используя цифры 3. 0, 2, 1 так, чтобы в первом множителе было     1203 · 2           2103 · 2          3 тысячи.

            1230 · 2           2130 · 2

            1302 · 2           2301 · 2

            1320 · 2           2310 · 2

10.Догадайся, как, не вычисляя значений произведений, выбрать из чисел, записанных справа, правильные ответы?

          12.678 · 3                                     45.030

        101.230 · 3                                    5.056

            1.495 · 4    38.034  Проверь себя, выполнив умножение столбиком.

            7.495 · 4  5.980

            1.013 · 5  303.690

            9.006 · 5  28.980      (29.980)

При выполнении 10-го задания учащиеся знакомятся с некоторыми способами «прикидки» результата.

Итак, процесс выполнения каждого задания, который направляется специальными вопросами, нацелен на развитие мыслительных операций. Развивающую функцию имеет не только каждое задание в отдельности, но и вся система в целом. Задания располагаются в определѐнной последовательности и связаны между собой. Имеет место постепенное усложнение заданий и повышение уровня самостоятельности учащихся в процессе их выполнения. Все задания рассматривают разные аспекты изучаемого вычислительного приѐма во взаимосвязи с ранее усвоенными знаниями, умениями и навыками и обеспечивают осознанное усвоение алгоритма.