МИНИСТЕРСТВО ПРОСВЕЩЕНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ

Федеральное государственное бюджетное образовательное учреждение

высшего профессионального образования

«Алтайский государственный гуманитарно-педагогический университет им. В.М. Шукшина»

(АГГПУ им. В.М. Шукшина)

Центр повышения квалификации и переподготовки

Решение практико-ориентированных задач по математике

в 7-м классе как инструмент развития функциональной грамотности обучающихся

Выпускная квалификационная работа

Бийск 2022

Содержание

Введение. 4

Глава 1.Теоретические основы развития функциональной грамотности школьников посредством решения практико-ориентированных задач. 10

1.1. Понятие функциональной грамотности в психолого-педагогической литературе  10

1.2. Особенности формирования функциональной грамотности учащихся. 11

1.3. Понятие практико-ориентированной задачи. 14

1.4. Решение практико-ориентированных задач  как инструмент развития функциональной грамотности обучающихся. 19

Выводы по I главе. 21

Глава II. Экспериментальное исследование по развитию функциональной грамотности у учащихся 7 класса посредством решения практико-ориентированных задач. 23

2.1. Организация и методы экспериментального исследования. 23

2.2. Изучение уровня знаний школьников в области решения практико-ориентированных задач. 25

2.3. Описание и реализация решения практико-ориентированных задач среди школьников для развития функциональной грамотности. 28

2.4. Оценка эффективности проведенной работы.. 34

Выводы по II главе. 37

Заключение. 39

Список использованной литературы.. 41

Приложение 1. Первичная диагностика уровня функциональной грамотности  45

Приложение 2. . Фрагменты уроков 7 класса, с использованием практико-ориентированных задач. 54

Приложение 3. Повторная  диагностика уровня функциональной грамотности  56

Введение

Актуальность исследования.

При комплексном подходе к анализу конкурентоспособности образования страны, который невозможно оценить вне контекста международных исследований качества образования, выделяются три типа индикаторов:

 — функционирование образовательной системы в целом (например, охват, финансирование, дифференциация);

 — характеристики образовательного процесса на уровне образовательных организаций (структура, условия, кадры, содержание, технологии);

 — образовательные результаты.

Образовательные результаты являются ключевым индикатором качества образования, так как именно через призму образовательных результатов рассматривается эффективность образовательной политики страны и определяется необходимость реформ в системе образования и их темпов. Именно результаты международных исследований PIRLS, вместо введения TIMSS, PISA служат целевыми показателями качества образования страны, которые отражены в Государственной программе РФ «Развитие образования» (2018-2025 годы) от 26 декабря 2017 года.

Существует несколько признанных организаций, проводящих независимую международную оценку уровня функциональной грамотности в более чем 60 странах мира:

— Международная ассоциация оценки образовательных достижений

— IEA (International Association for the Evaluation of Educational Achievements);

 — Международное сравнительное исследование качества математического и естественно-научного образования

 — TIMSS (Trends in Mathematics and Science Study);

 — Международная оценка образовательных достижений учащихся

 — PISA (Programme for International Student Assessment).

Основной целью первых двух организаций является проверка определенных школьными программами предметных знаний и умений с помощью выполнения учебных заданий, мало или совсем не связанных с реальной жизнью. Особый интерес в этом ряду представляет исследование PISA, в программе которой впервые реализуется компетентностный подход в оценке образовательных достижений. Исследование PISA ставит своей целью проверку наличия таких умений, т. е. проверку подготовки молодежи к «взрослой» жизни, что отличает его от других.

Международное исследование PISA представляет функциональную грамотность в виде составляющих:

— грамотность в чтении

— способность человека к пониманию письменных текстов и рефлексии на них, к использованию их содержания для достижения собственных целей, развития знаний и возможностей, для активного участия в жизни общества;

 — грамотность в математике

 — способность человека определять и понимать роль математики в мире, в котором он живет, высказывать хорошо обоснованные математические суждения и использовать математику так, чтобы удовлетворять в настоящем и будущем потребности, присущие созидательному, заинтересованному и мыслящему гражданину;

— грамотность в области естествознания

— способность использовать естественно-научные знания для выделения в реальных ситуациях проблем, которые могут быть исследованы и решены с помощью научных методов для получения выводов, основанных на наблюдениях и экспериментах. Эти выводы необходимы для понимания окружающего мира и тех изменений, которые вносит в него деятельность человека, и для принятия соответствующего решения.

 С 2012 года отдельным направлением оценки была включена финансовая грамотность, которая подразумевает знание и понимание финансовых понятий и финансовых рисков, а также навыки, мотивацию и уверенность, необходимые для принятия эффективных решений в разнообразных финансовых ситуациях, способствующих улучшению финансового благополучия личности и общества, а также возможности участия в экономической жизни.

Российская система образования в 2016 году занимала 34 место как по первому рейтингу (из 188 стран), так и по второму рейтингу (из 50 стран). Основной причиной невысокого рейтинга России являются низкие результаты российских учащихся пятнадцатилетнего возраста практически по всем областям функциональной грамотности, выявленные в исследовании PISA. Речь идет, прежде всего, о недостаточно сформированной способности у учащихся использовать имеющиеся предметные знания и умения при решении задач, приближенных к реальным ситуациям, а также невысокий уровень владения такими умениями, как поиск новых или альтернативных способов решения задач, проведения исследований или групповых проектов.

 Другими словами, относительный неуспех наших школьников в решении заданий, предлагаемых в международных кроется в отсутствии практики решения задач, направленных на развитие функциональной грамотности обучающихся в отечественной школе.

Функциональная грамотность показывает, насколько обучающийся может использовать полученные знания, умения и навыки в реальных жизненных ситуациях. Она фиксирует минимально необходимый уровень готовности личности для осуществления ее жизнедеятельности в конкретной культурной среде.

 Важно отметить, что становление функциональной грамотности происходит в образовательном процессе, который построен в методологии компетентностного подхода. В настоящее время задания на развитие функциональной грамотности не находят широкого применения в практике российской школы. Все инструменты оценивания результатов образования внутри страны (среди них важнейшие — ОГЭ и ЕГЭ) направлены, главным образом, на оценку предметного знания, зачастую сводящегося к знанию фактов, и на оценку умения решать типовые (стандартные) задачи. Они не оценивают компетентность как умение действовать в определенной ситуации.

Уточним, что под компетентностью понимается способность эффективно мобилизовывать, т. е. выбирать и использовать наиболее подходящие знания и умения для решения задач, в том числе в новых нестандартных ситуациях. Важно отметить и недостаточную подготовку учителей в области формирования функциональной грамотности, а также отсутствие необходимых учебно-методических материалов.

Цель исследования – повышение функциональной грамотности обучающихся посредством решения практико-ориентированных задач.

Объект исследования – функциональная грамотность обучающихся.

Предмет исследования – методика решения практико-ориентированных задач по математике как инструмент развития функциональной грамотности.

Задачи исследования:

1.                 Изучить психолого-педагогическую литературу по проблеме исследования.

2.                 Изучить функциональную грамотность школьников в естественно-научном образовании.

3.                 Разработать и реализовать проект с целью развития функциональной грамотности школьников в области математики.

4.                  Оценить эффективность проектной деятельности для развития функциональной грамотности школьников в области математики.

Гипотеза исследования:

Решение практико-ориентированных задач способствует повышению уровня функциональной математической грамотности.

Методы исследования:

1)                Теоретические методы (анализ психолого-педагогической, методической литературы по проблеме исследования; обобщение).

2)                Эмпирические методы (оценка уровня функциональной грамотности; психолого-педагогический эксперимент (констатирующий, формирующий и контрольный этапы)).

3)                Метод количественной и качественной обработки данных.

Практическая значимость исследования заключается в том, что разработанные занятия для школьников может быть использован в практике учителей математики, а содержание выпускной квалификационной работы представляет интерес для студентов при подготовке курсовой работы, подготовки к практических  по дисциплине – методика обучения математики.

Экспериментальная база исследования. Экспериментальное исследование проводилось на базе Муниципального бюджетного образовательного учреждения «Быстроистокская общеобразовательная средняя школа) (МБОУ «БОСШ») Алтайского края. В эксперименте принимали участие школьники 7-го класса. Всего 40 человек: 20 школьников в контрольной группе и в 20 обучающихся экспериментальной группы.

Структура ВКР. Выпускная квалификационная работа состоит из введения, двух глав, заключения, списка литературы и приложения.

Во введении отражены актуальность исследования, представлены цель, предмет, объект, гипотеза и задачи исследования; определены методы и экспериментальная база исследования; показана практическая значимость.

В первой теоретической главе раскрыта проблема развития функциональной грамотности обучающихся, понятие и решение практико-ориентированных задач.

Во второй главе (практической) представлены описание и результаты экспериментального исследования по развитию функциональной грамотности школьников посредством решения практико-ориентированных задач.

В заключении сформулированы выводы по результатам исследования.

Список литературы представлен 32 литературными источниками.

В приложениях представлен материал для проведения диагностики функциональной грамотности школьников, а также описание практико-ориентированных задач.

Глава 1.Теоретические основы развития функциональной грамотности школьников посредством решения практико-ориентированных задач

В данной главе рассмотрены основные понятия, связанные с темой исследования: функциональная грамотность, практико-ориентированная задача и т.д.. Также описаны особенности формирования функциональной грамотности у учащихся и взаимосвязь функциональной грамотности и практико-ориентированных задач.

1.1. Понятие функциональной грамотности в психолого-педагогической литературе

Леонтьев А.А.: «Функционально грамотный человек — это человек, который способен использовать все постоянно приобретаемые в течение жизни знания, умения и навыки для решения максимально широкого диапазона жизненных задач в различных сферах человеческой деятельности, общения и социальных отношений» [1]

Новый словарь методических терминов и понятий: «ФУНКЦИОНАЛЬНАЯ ГРАМОТНОСТЬ. Способность человека вступать в отношения с внешней средой и максимально быстро адаптироваться и функционировать в ней. В отличие от элементарной грамотности как способности личности читать, понимать, составлять короткие тексты и осуществлять простейшие арифметические действия, Ф.г. есть уровень знаний, умений и навыков, обеспечивающий нормальное функционирование личности в системе социальных отношений, который считается минимально необходимым для осуществления жизнедеятельности личности в конкретной культурной среде» [2].

Виноградова Н.Ф.: «Функциональная грамотность сегодня — это базовое образование личности Ребенок должен обладать: - готовностью успешно взаимодействовать с изменяющимся окружающим миром …; - возможностью решать различные (в том числе нестандартные) учебные и жизненные задачи…; - способностью строить социальные отношения…; - совокупностью рефлексивных умений, обеспечивающих оценку своей грамотности, стремление к дальнейшему образованию…» [3].

Определение функциональной грамотности в исследовании PISA заложено в основном вопросе, на который отвечает исследование: «Обладают ли учащиеся 15-летнего возраста, получившие обязательное общее образование, знаниями и умениями, необходимыми им для полноценного функционирования в современном обществе, т.е. для решения широкого диапазона задач в различных сферах человеческой деятельности, общения и социальных отношений?» [4]

1.2. Особенности формирования функциональной грамотности учащихся

Словарь терминов современного педагога трактует понятие о функциональной грамотности следующим образом: «Умение человека грамотно, квалифицированно функционировать во всех сферах человеческой деятельности: работе, государстве, семье, здоровье, праве, политике, культуре».

Функциональная грамотность — это индикатор общественного благополучия. В ближайшем будущем функциональная грамотность станет показателем развитости цивилизации, государства, нации, социальной группы, отдельной личности.

Высокий уровень указывает на социокультурные достижения общества; низкий — предостережением возможного социального кризиса, результатом которого могут быть: низкая способность к социальной адаптации; неумение выстраивать парадигму своих взаимоотношений в семье, в трудовом коллективе; незнание своих прав и обязанностей.

 Поэтому для школы возникает очень важная цель: подготовить не отдельных элитных учащихся к жизни, а обучить мобильную личность, способной при необходимости быстро менять профессию, осваивать новые социальные роли и функции, быть конкурентоспособным. Так для современного мира особую актуальность приобретает исследование уровня функциональной грамотности учащихся, т. к. все эти функциональные навыки формируются именно в школе. И одной из основных задач школьного образования сегодня — подготовить учащегося к адаптации в современном мире [5]

 Базовым навыком функциональной грамотности является математическая грамотность. В современном обществе умение логически рассуждать, анализировать информацию и решать проблемы становится обязательным условием успешности. Таким образом, обобщая вышесказанное, функциональная грамотность — способность человека, общества вступать в отношения с внешней средой и умение быстро адаптироваться в изменяющихся условиях.

   С функциональной грамотностью связаны компетенции:            

 1) Способность выбирать и использовать различные технологии.              

 2) Способность видеть проблемы и искать пути их решения.           

 3) Способность учиться всю жизнь.

 Главное же понятие функциональной грамотности заключается в воспитании человека в духе доброжелательности и дружелюбия, что обеспечивает культуру общения[6].

Разумеется, функциональная грамотность в сфере социальных отношений ни в коей мере не может стать единственной целью образования. Но оно дает возможности для формирования творческого опыта и способностей.

Со стороны государства, учитывая важность и значимость развития функциональной грамотности, предприняты серьезные действия относительно обновления содержания образования. Впервые за всю историю будут разработаны проекты поддержки организаций дополнительного образования. Формирование и развитие функциональной грамотности учащихся поставлено Главой государства приоритетной задачей.

Для этого в стране предприняты необходимые меры. Будет обеспечен переход от фронтальных форм обучения классного коллектива к реализации индивидуальной образовательной траектории каждого учащегося, в том числе с использованием интерактивных, инновационных, проектно-исследовательских технологий, цифровой инфраструктуры. Решение многих задач зависит от профессионализма педагогических кадров. Сильным потенциалом школы должен стать её учительский корпус.

 Педагог должен быть готов использовать средства информатизации и информационные технологии в обучении, в воспитании и развитии своих учеников. Чтобы формировать информационную культуру у учащихся, учитель и сам должен обладать такой культурой. Каждый педагог должен понимать свою роль в становлении личности. Личная увлеченность учителя порождает успех во внедрении образовательных реформ.

 21 век дает заказ на выпускников, обладающих вероятностным мышлением, то есть способных ориентироваться в незнакомой ситуации. Поэтому назрела необходимость внедрения в учебный процесс инновационных методик и новых педагогических технологий, призванных обеспечить индивидуализацию обучения и воспитания, развивать самостоятельность учащихся, а также содействовать сохранению и укреплению здоровья.

Для современной системы образования актуальным становится, наряду с использованием достижений отечественной педагогики, зарубежный опыт, содержащий идеи гуманистически ориентированной педагогики. На основе кембриджского опыта идет массовая апробация новых подходов в обучении, что, несомненно, играет позитивную роль.

Одним из ведущих предметов в системе школьного образования является математика. Цель учителей:  научить мыслить, анализировать и решать различные проблемные ситуации.

В задачах учителя не преподносить знания школьникам, а создать условия самостоятельного добывания знаний. Нужно следовать мудрой пословице: «Давать не рыбу, а удочку».

Нынешние учащиеся обладают прагматичностью мыслей, раскрепощенностью и независимостью, а эти перемены способствуют формированию практических умений.

Теперь в основу уроков должны быть положены социально-конструируемые педагогические ситуации, деятельность учащихся в которых и будет воспитывать требуемые качества личности.

Например, умение брать ответственность на себя, принимать решение, действовать и работать в коллективе ведомым и ведущим, выдвигать гипотезы, критиковать, оказывать помощь другим, умение обучаться и многое другое. Трудностей немало, но уже видны конкретные пути их преодоления.

 По мере развития науки и техники, требования к знаниям растут, расширяется их диапазон, формируются новые качественные признаки. Поэтому можно сказать, что функциональная грамотность человека выступает показателем его способности адаптироваться к условиям микросоциума.

Для формирования функциональной грамотности необходимо создать особую образовательную среду, причем не только на уроке, но и во внеурочное время. Дети приходят в школу самые разные: собранные и несобранные, внимательные и рассеянные, быстро схватывающие и медлительные, неряшливые и аккуратные. Едины они в одном. Все дети без исключения приходят в школу с искренним желанием хорошо учиться.

Красивое человеческое желание — хорошо учиться — озаряет весь смысл школьной жизни детей. Нет сильных или слабых — есть заинтересованные. Очень часто даже слабые обладают оригинальностью идей.

Педагогам, надо поддержать, развить человека в человеке, помочь человеку жить в мире и согласии с людьми, природой, культурой, цивилизацией, так как школа, на мой взгляд, в современном мире является, пожалуй, единственным и очень важным серьёзным источником формирования функциональной грамотности.

1.3. Понятие практико-ориентированной задачи

В настоящее время широко применяется термин «задача», как в жизни, так и в науке. Этим термином обозначаются многие и весьма различные понятия, но на сегодняшний день нет общего определения понятия «задача».

В учебно-педагогической литературе встречаются самые разнообразные подходы к понятию задачи. Титова Е. И считает, что наиболее простое определение задачи, было дано известным педагогом-математиком С. О. Шатуновским. Оно гласит: «Задача есть изложение требования «найти» по «данным» вещам другие «искомые» вещи, находящиеся друг к другу и к данным вещам в указанных соотношениях». При этом предполагается, что понятия «вещь», «найти», «данные», «искомые» в каждом отдельном случае особо определяются[14].

В широком смысле задача рассматривается как проблемная ситуация с явно заданной целью, которую необходимо достичь. В более узком смысле задачей также называют саму эту цель, данную в рамках проблемной ситуации, то есть то, что требуется сделать.

В словаре Ожегова определение задачи звучит следующим образом:

«Задача - то, что требует исполнения, разрешения. Это упражнение, которое выполняется посредством умозаключения, вычисления».

Т.Ф. Ефремова под задачей предлагает:

§     Цель, к которой стремятся, которую хотят достичь.

§     Обстоятельства, затруднения, которые надо преодолеть.

§     Поручение, задание (обычно трудно выполнимые, сложные).

§     Вопрос (обычно математического характера), требующий

·                   нахождения решения по известным данным с соблюдением определенных условий[32].

Д. Пойа, рассматривая роль задач в математике, писал: «Что значит владение математикой?  Это есть умение решать задачи, причем не только стандартные, но и требующие известной независимости мышления, здравого смысла, оригинальности, изобретательности»[30].

Мы считаем, что одним из главных составляющих содержания учебного предмета математики, являются математические задачи, при помощи которых, учащиеся лучше усваивают теоретический материал. Поэтому решение задач является основной деятельностью при обучении математике[31].

Проанализировав различные трактовки понятия «задача» Г.А. Балл

выделил свои определения. Он выделяет три подхода к характеристике понятия «задача»:

·                   Задача – есть ситуация, требующая от субъекта некоторого действия.

·                   Мыслительная задача – ситуация, требующая от субъекта некоторого действия, направленного на нахождение неизвестного

·                   Проблемная задача (или проблема) – ситуация, требующая от субъекта некоторого действия, направленного на нахождение неизвестного на основе пользования его связей с известным в условиях, когда субъект не обладает способом (алгоритмом) этого действия [13].

Ю.М. Колягин отмечает, что решение задач является важнейшим видом деятельности и называется этот вид деятельности – математическим. Он в своих работах рассматривает сложную систему и утверждает, что без субъекта (человека) и объекта – некоторого множества нет задачи.

Чётко выражает свою точку зрения Л.М. Фридман. Для него задача является проблемной ситуацией, которая выражается с помощью знаков естественного или научного языка. Он считает, что если субъект при выполнении какой–либо деятельности на своём пути встречает трудности, то в результате возникает проблемная ситуация. Значит проблемная ситуация – это не просто трудности, возникающие на пути субъекта, а его желание и стремление их устранить. Поэтому, субъект является элементом задачи, осознавший затруднение в своей деятельности [27].

Л.М. Фридман четко различает понятие задачи и проблемной ситуации по следующим признакам:

Проблемная ситуация всегда богаче содержанием, чем задача, ибо задача – это модель ситуации, отражающая лишь некоторые ее стороны;

Для каждой проблемной ситуации существует одна или несколько задач, которые могут отличаться друг от друга как совокупностью представленных в них свойств ситуации, так и языком, на котором задача

выражена;

 Проблемная ситуация существует реально, вне зависимости от какого-либо языка, а задача всегда связана с языком, на котором она изложена[25].

Таким образом, в своей работе под термином «задача» будем рассматривать проблемную ситуацию, включающую цель и условия для ее достижения[24].

Как считали методисты–математики Д. Пойа, Л.М. Фридмана, Г.И. Саранцева, и психолог В.В. Давыдов, формировать способность разрешения проблем помогают специальным образом подобранные задачи.

В своей работе будем называть их практико-ориентированными задачами. Под практико-ориентированной задачей понимается, прежде всего, текстовая математическая задача, в которой выделяется четыре основных части

1) условие – начальное состояние;

2) базис решения – теоретические основы решения;

3) решение – преобразование условия задачи для нахождения,

требуемого;

4) заключение – конечное состояние.

Практико-ориентированные задачи – это задачи из окружающей действительности, которые тесно связанны с формированием практических навыков, необходимых в повседневной жизни[10].

Цель этих задач – формирование умений действовать в социально-значимой ситуации. Практико-ориентированные задачи помогают учащимся работать с информацией, выделять и отбирать главное, выстраивать собственные пути решения и обосновывать их, работать в парах и в группах, развить свои точки зрения, чувства, убеждения и желания в поисковой творческой деятельности учащихся [11].

Виды практико-ориентированных заданий:

 Аналитические – это определение и анализ цели, выбор и анализ

условий и способов решения, средств достижения цели;

 Организационно – подготовительные – это планирование и организация практико-ориентированной работы индивидуальной, групповой или коллективной по созданию объектов; анализ и исследование свойств объектов труда, формирование понятий и установление связей между ними.

 Оценочно-коррекционные – это формирование действий оценки и

коррекции процесса и результатов деятельности, поиск способов совершенствования, анализ деятельности [12].

Исторически сложились две стороны назначения математического образования: практическая, связанная с созданием и применением инструментария, необходимого человеку в его деятельности, и духовная, связанная с мышлением человека, с овладением определенным методом познания и преобразования мира математическим методом. В настоящее время для человека чрезвычайно важно не столько энциклопедическая грамотность, сколько способность применять обобщённые знания и умения для разрешения конкретных ситуаций и проблем, возникающих в реальной действительности. Формировать способность разрешения проблем помогают специальным образом подобранные задачи – практико-ориентированные[21].

Одной из характеристик практико-ориентированных задач является их нестандартность, т.е. в структуре задачи неопределенны некоторые из ее компонентов. Другой особенность является присутствие различной степень рациональности – это наличие нескольких способов решения задачи. Также в задаче достаточно объёмная формулировка условий при наличии избыточных или недостающих данных.

Как показывает практика, технология обучения с применением практико-ориентированных заданий, позволяет ученика из пассивного объекта педагогического воздействия превратить в активного субъекта учебно-познавательной деятельности.

Постоянное применение практико-ориентированных задач при обучении математики в школе, позволит учащемуся закрепить и углубить теоретические знания, овладеть умениями и навыками по учебной дисциплине, уметь связывать учебный процесс с реальными жизненными условиями, проявлять инициативу и самостоятельность

1.4. Решение практико-ориентированных задач  как инструмент развития функциональной грамотности обучающихся

Одним из важнейших элементов в формировании и развитии математической грамотности учащихся являются практико-ориентированные задачи.

Под практико-ориентированной задачей понимается математическая задача, в содержании которой описывается ситуация из окружающей действительности, связанная с формированием у учащихся практических навыков использования математических знаний и умений, необходимых в повседневной жизни, в том числе, с использованием материалов краеведения и элементов производственных процессов [9].

Решение практико-ориентированных задач в большей степени строится на построении модели реальной ситуации, описанной в конкретной задаче. У практико-ориентированных задач есть свои особенности, которых отличают их от других математических задач, а именно:

 − значимость (общекультурная, познавательная, профессиональная, социальная) получаемого результата, что обеспечивает познавательную мотивацию учащегося);

− условие задачи сформулировано как сюжет, ситуация или проблема, для разрешения которой необходимо использовать знания из разных разделов основного предмета — математики, из другого предмета или из жизни, на которые нет явного указания в тексте задачи;

− информация и данные в задаче могут быть представлены в различной форме (рисунок, таблица, схема, диаграмма, график и т. д.), что потребует распознавания объектов;

− указание (явное или неявное) области применения результата решения.

Кроме этих обязательных особенностей, практико-ориентированные задачи могут иметь еще и следующие:

− нестандартная структура (когда некоторые элементы не определены);

− наличие избыточных, недостающих и противоречивых данных в условии, делающих его объемным;

− наличие нескольких способов решения, причем, не все из них могут быть известны учащимся.

Виды практико-ориентированных заданий по математике:

−  аналитические (определение и анализ цели);

− организационно-подготовительные (планирование и организация индивидуальной, групповой или коллективной работы по созданию объектов, анализ и исследование свойств объектов труда);

− оценочно-коррекционные (сформировать оценку действиям и осуществить коррекцию процесса и результатов деятельности, провести небольшой поиск способов совершенствования деятельности) [8].

Математическая грамотность и практико-ориентированные задачи неразрывно связаны. Это связь проявляется уже в самом понятии математической грамотности, как способности учащихся:

 − распознавать проблемы, возникающие в окружающей действительности и которые можно решить средствами математики;

 − формулировать эти проблемы на языке математики;

 − решать эти проблемы, используя математические факты и методы;

 − анализировать использованные методы решения;

 − интерпретировать полученные результаты с учетом поставленной проблемы;

− формулировать и записывать результаты решения. Лучший тренажер математической грамотности

— это решение практико-ориентированных задач[7]

Решение практико-ориентированных задач, может создать такие положительные результаты, как:

− повышенная мотивация учеников к получению новых знаний;

 − более осмысленное освоение нового материала;

 − стремление к творческой и исследовательской деятельности;

 − приобретение навыков самостоятельной и коллективной работы в рамках проектов;

− осознание учащимися важности математики, как науки, приносящей реальную пользу в повседневной жизни[19].

Постоянная работа по решению практико-ориентированных задач на уроках математики  поспособствуют повышению уровня математической грамотности учащийся, и подготавливая их не только к успешной сдаче ОГЭ, где пять заданий являются практико-ориентированными, но и давая ценные навыки по применению математических знаний в реальной жизни[20].

Выводы по I главе

 По мнению Леонтьева А.А.: «Функционально грамотный человек — это человек, который способен использовать все постоянно приобретаемые в течение жизни знания, умения и навыки для решения максимально широкого диапазона жизненных задач в различных сферах человеческой деятельности, общения и социальных отношений»

Рассматривая функциональную математическую грамотность можно сделать вывод, что для решения проблемы математически грамотный учащийся сначала должен увидеть математическую природу проблемы, представленной в контексте реального мира, и сформулировать ее на языке математики.

Это преобразование требует математических рассуждений и, возможно, является центральным компонентом того, что значит быть математически грамотным. Это один из навыков XXI века.

В настоящее время школа пока ещё продолжает ориентироваться на обучение, выпуская в жизнь человека обученного, но тогда как сегодняшнее, информационное общество запрашивает человека обучающегося, способного самостоятельно учиться и готового к реальным действиям и принятию решений.

Это определяет значимость математики в формировании у учащихся умений решать задачи, возникающие в процессе практической деятельности человека.

Глава II. Экспериментальное исследование по развитию функциональной грамотности у учащихся 7 класса посредством решения практико-ориентированных задач

В данной главе описаны результаты экспериментального исследования проведенного с 7-классниками.

2.1. Организация и методы экспериментального исследования

Цель исследования – изучение и развитие функциональной грамотности обучающихся посредством решения практико-ориентированных задач.

Гипотеза исследования - решение практико-ориентированных задач способствует повышению уровня функциональной математической грамотности.

Задачи исследования:

1.                 Изучить психолого-педагогическую литературу по проблеме исследования.

2.                 Изучить функциональную грамотность школьников.

3.                 Разработать и реализовать проект с целью развития функциональной грамотности школьников.

4.                 Оценить эффективность данной деятельности для развития функциональной грамотности школьников.

Экспериментальное исследование проводилось на базе Муниципального бюджетного образовательного учреждения «Быстроистокская общеобразовательная средняя школа) (МБОУ «БОСШ»)  Алтайского края. В эксперименте принимали участие школьники 7-го класса. Всего 40 человек: 20 школьников в контрольной группе и в 20 обучающихся экспериментальной группы.

Экспериментальная группа – это группа, непосредственно подвергающаяся экспериментальному воздействию в процессе исследования, то есть группа, с которой непосредственно работает экспериментатор.

Контрольная группа помещается в те же условия, что и экспериментальная, за исключением того, что испытуемые в ней не подвергаются экспериментальному воздействию.

Экспериментальное исследование проводилось в три этапа:

1.      Констатирующий этап

Данный этап посвящен выбору методики для определения уровня функциональной грамотности учащихся и диагностике учащихся контрольной и экспериментальной групп.

2. Формирующий этап

На данном этапе разработана и реализована деятельность в экспериментальной группе школьников.

3. Контрольный этап

На данном этапе проведена повторная диагностика уровня функциональной грамотности школьников контрольной и экспериментальной групп. Проведен сравнительный анализ результатов диагностики уровня функциональной грамотности  школьников в обеих группах на констатирующем и контрольном этапах с целью выявления динамики уровня функциональной грамотности и определения эффективности практико-ориентированных задач  для развития функциональной грамотности учащихся 7 класса.

Для проведения экспериментального исследования были использованы следующие методы:

1)      Анализ учебно-методических источников (анализ образовательной программы для 7-го класса для определения возможности реализации практико-ориентированных на уроках математики).

2)      Педагогический эксперимент (констатирующий, формирующий и контрольный этапы);

3)      Статистические методы (обработка результатов эксперимента).

2.2. Изучение уровня знаний школьников в области решения практико-ориентированных задач

Цель констатирующего этапа – определение уровня знаний школьников в области решения практико-ориентированных задач

Задачи констатирующего этапа:

1)                подобрать методику для диагностики уровня функциональной грамотности, соответствующую возрастным особенностям школьников;

2)                провести оценку уровня функциональной грамотности школьников контрольной и экспериментальной групп;

3)                проанализировать результаты диагностики уровня функциональной грамотности школьников.

Для проведения диагностики уровня функциональной грамотности учащихся 7 класса была выбрана методика, состоящая из ряда практико-ориентированных задач (Приложение 1)

Методика представляет собой проверочную работу по математической грамотности, разработанная при министерстве просвещения Российской Федерации. Каждый ответ оценивается определенным количеством баллов в соответствии с ответам к задачам.

Данные задачи были использованы для групповой диагностики. При этом задачи в напечатанном виде раздавались всем ученикам, и экспериментатор просил их решить их. Такой вариант предъявления позволяет получить более точные ответы и выявить логику решения задачи, и доступен для учеников 7 класса, когда дети уже хорошо читают, пишут, решают и анализируют задачи.

Методика позволяет определить уровни функциональной грамотности

Первый уровень.

40-50 баллов – высокий уровень функциональной грамотности.

У таких детей есть познавательный мотив, стремление наиболее успешно выполнять все предъявляемые школой требования. Ученики четко следуют всем указаниям учителя, добросовестны и ответственны, сильно переживают, если получают неудовлетворительные оценки.

Второй уровень.

30-40 балла – уровень функциональной грамотности выше среднего..

Подобные показатели имеют большинство учащихся, успешно справляющихся с учебной деятельностью. При ответах на вопросы проявляют меньшую зависимость от жестких требований и норм. Подобный уровень функциональной грамотности является средней нормой.

Третий уровень.

15-30 баллов – средний уровень функциональной грамотности.

Такие дети достаточно благополучно обучаются в школе, однако это лишь на уровне «зазубрить-сдать». Им тяжело адаптироваться к жизненной ситуации, без определенного алгоритма.

Четвертый уровень.

0-15  баллов – низкий уровень функциональной грамотности.

Эти дети могут благополучно обучаться, но совершенно не могут приспосабливаться и анализировать ситуацию. Но чаще учебные показатели у этих школьников, также ниже нормы.

Для удобства обработки результатов и их наглядного представления дадим следующие названия вышеописанных уровней учебной мотивации:

Первый уровень – высокий уровень функциональной грамотности.

Второй уровень – уровень функциональной грамотности выше среднего.

Третий уровень – средний уровень функциональной грамотности.

Четвертый уровень – низкий уровень функциональной грамотности.

Условия обучения в обеих группах, контрольной и экспериментальной, одинаковы, что позволяет считать их равнозначными и допустить к участию в эксперименте.

Представим результаты диагностики уровня функциональной грамотности  школьников контрольной и экспериментальной групп на констатирующем этапе в таблице 1 и на рисунке 1.

Таблица 1

Результаты диагностики уровня функциональной грамотности школьников контрольной и экспериментальной групп на констатирующем этапе

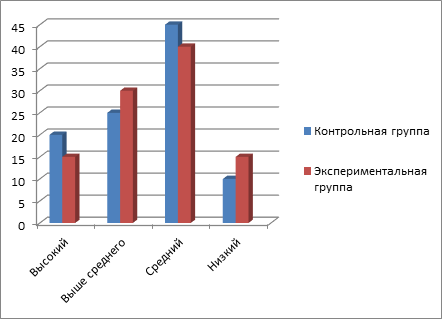
Рис. 1. Результаты диагностики уровня функциональной грамотности школьников контрольной и экспериментальной групп на констатирующем этапе

Вывод:  Проведя диагностику можно сделать вывод о том, что дети в контрольной и экспериментальной группах имеют примерно равный уровень функциональной грамотности

2.3. Описание и реализация решения практико-ориентированных задач среди школьников для развития функциональной грамотности

Цель формирующего этапа экспериментального исследования – разработка и реализация  занятий для развития функциональной грамотности учащихся 7 класса.

Задачи формирующего этапа:

1)      разработать и реализовать занятия в соответствии с возрастом учащихся и образовательной программой для 7 класса;

2)      организовать деятельность школьников экспериментальной группы, связанную с решением практико-ориентированных задач.

Мероприятие разработанное в ходе исследования:

План проведения внеклассного мероприятия

«Один день из жизни семьи»

Цели урока:

- Научиться решать некоторые задачи, с которыми каждый из нас  может столкнуться в повседневной жизни.

- Опровергнуть  мнение, что не всем нужно учиться математике;

Оборудование: мультимедиа проектор.

Ход занятия

I. Организационный этап. Сообщение темы  и цели  занятия.

Учитель:  

Как часто приходится слышать: «Зачем мне учить математику?  Я серьезно занимаюсь спортом, музыкой, рисую, пою, фотографирую, строгаю, выпиливаю и т. д. и т. п.  Я не собираюсь становиться математиком или физиком, программистом  или инженером-конструктором. А кто-то из девочек, глядя на своих мам, скажет, что будет домохозяйкой…

II. Решение  задач.

Учитель:

Рассмотрим один день из  жизни семьи, состоящей из пяти человек:  бабушки, мамы, папы, и двух детей, старшей дочери Ани и ее брата Вити.

Утром мама, провожая Витю, дала ему деньги и попросила зайти после школы в аптеку и купить лекарство для бабушки, а когда пойдет гулять,  разрешила купить на сдачу сок себе и друзьям.

Слайд:  Задача  № 1.  

Больному прописано лекарство, которое нужно пить по 0,5 г  3 раза в день в течение 8 дней. В одной упаковке 10 таблеток лекарства по 0,25 г. Какого наименьшего количества упаковок хватит на весь курс лечения? (ученик решает задачу на доске и комментирует решение вслух)[17]

Слайд:  Решение (проверка)

 1)  0,5 · 3 · 8 = 12 (г) лекарства нужно на курс лечения    

2)  0,25 · 10 = 2,5 (г) лекарства в 1 упаковке  

3)  12 : 2,5 = 4,8 (упаковок)  

На курс лечения потребуется купить не менее 5 упаковок лекарства.

Ответ: 5 упаковок.

Слайд:   Задача  № 2.  

 Пакетик сока стоит 14 рублей 50 копеек. Какое наибольшее число пакетиков сока можно купить на 100 рублей?  (Хватит ли денег Вите, если он захочет купить сок себе и угостить пятерых друзей; если «да», то сколько денег у него останется?) (ученик решает задачу  на месте и комментирует решение вслух)[15]

Слайд:  Решение

1) 100 : 14,5 = 1000 : 145 = 6,8… (п.)

На 100 руб. можно купить не более 6 пакетиков сока.

Да, Вите хватит денег.

2)  100 – 14,5 · 6 = 100 – 87 = 13 (руб.)

Ответ: 6 пакетиков сока;

            останется 13 рублей.

Учитель:

Обратите внимание, что в решенной задаче округление выполняется с недостатком, хотя по правилам округления должно быть с избытком.

Учитель:

Дочь Аня для поездок в институт использует проездной билет.

Слайд:  Задача  № 3.

 Аня купила месячный проездной билет на автобус. За месяц она сделала 45 поездок. Сколько рублей она сэкономила, если проездной билет стоит  750 рублей, а разовая поездка  25 рублей? 28 рублей? (ученик решает задачу на доске и комментирует решение вслух)[22]

Слайд: Решение

1) 25 · 45 =1125 (руб.) стоимость 45 поездок по 25 руб.

    1125 – 750 = 375 (руб.) экономия    

2) 28 · 45 = 1260 (руб.) стоимость 45 поездок по 28 руб.

     1260 – 750 = 510 (руб.) экономия  

Ответ:  375 руб.;  510 руб.

Учитель:

После занятий Аня зашла в Торговый Центр, чтобы купить             что-нибудь к чаю.

Слайд:  Задача  № 4.  

 В супермаркете проходит рекламная акция: заплатив за две шоколадки, покупатель получает три шоколадки (одна шоколадка в подарок). Шоколадка стоит 36 рублей.  Какое наибольшее число шоколадок можно получить на 200 рублей? (ученик решает задачу  на месте и комментирует решение вслух)[29]

Слайд:  Решение

200 : 36 = 5,5… (шоколадок)

    5 шоколадок можно купить на 200 рулей

 (округление с недостатком по смыслу задачи)

    + 2 шоколадки  в подарок

    Всего 7 шоколадок.

Ответ:  7 шоколадок.

Учитель:

Далее, проходя мимо «Салона сотовой связи», Аня увидела объявление о снижении стоимости SMS-сообщений в предпраздничные и праздничные дни.

Слайд:  Задача  № 5.    

 Аня отправила SMS-сообщения к 8 марта  своим  26 подругам. Стоимость одного  SMS-сообщения 1 рубль 20 копеек. Перед отправкой сообщений у Ани оставалось 50 рублей. Сколько рублей останется у Ани после отправки всех сообщений? (ученик решает задачу на доске и комментирует решение вслух)

Слайд:  Решение

1) 1 руб. 20 коп. = 1,2 руб.

2) 26 · 1,2 = 31,2 (руб.) стоимость 26  SMS-сообщений  

3) 50 – 31,2 = 18,8 = 18 руб. 80 коп. останется у Ани  

Ответ:  18 руб. 80 коп.

Учитель:

Папа, который в это время был в отпуске, решил сделать маме сюрприз и купил  42 рулона обоев для ремонта.

Слайд:  Задача  № 6.

 Для ремонта квартиры купили 42 рулона обоев. Сколько пачек обойного клея нужно купить, если одна пачка клея рассчитана на 8 рулонов? (ученик решает задачу  на месте и комментирует решение вслух)[16]

Слайд: Решение

42 : 8 = 5,25 (пачек)

6 пачек клея нужно купить

Ответ: 6 пачек.

Учитель:

Тем временем мама, во время обеденного перерыва, разговорилась с коллегами  о популярных тарифных планах телефонных компаний и узнала, что…

Слайд:  Задача № 7.  

Телефонная компания предоставляет  на выбор три тарифных плана.

 Абонент выбрал наиболее дешевый тарифный план, исходя из предположения, что общая длительность телефонных разговоров составит 800 минут в месяц. Какую сумму он должен заплатить за месяц, если общая длительность разговоров в этом месяце действительно будет равна 800 минутам? Ответ дайте в рублях. (ученик решает задачу на доске и комментирует решение вслух)[16]

Слайд: Решение

1) 800 · 0,35 = 280 (руб.) стоимость 800 минут по 1 тарифу

2) 800 – 350 = 450 (мин.)

     450 · 0,3 = 135 (руб.)    

     140 + 135 = 275 (руб.) стоимость 800 минут по 2 тарифу    

3) 300 руб. стоимость 800 минут по 3 тарифу.

 Ответ:  275 рублей. 

Учитель:

Вечером все собрались за ужином и, обсуждая планы на лето, решили поехать отдохнуть к морю. Бабушка решила остаться на даче.

Слайд:  Задача  № 8.    

 Семья из четырех человек планирует поездку из Москвы в Анапу. Можно ехать поездом, а можно – на своей машине.  Билет на поезд на одного человека стоит 1510 рублей. Автомобиль расходует 11 литров бензина на 100 километров пути, расстояние по шоссе равно 1500 км, а цена бензина  - 30 руб. за литр. Сколько рублей будет стоить самая дешевая поездка для этой семьи

а) Если поедут все четверо;

б) Если поедут трое?

 (ученик решает задачу на доске и комментирует решение вслух)[16]

Слайд:  Решение

а) На поезде, 3 человека:    1510 · 3 = 4530 (руб.)    

б) На поезде, 4 человека:    1510 · 4 = 6040 (руб.)

        На машине: 

100 км   --  11 литров

1500 км --  11 · 15 = 165 (литров) на всю дорогу

165 · 30 = 4950 (руб.) стоимость поездки на машине

  Ответ:  а) выгоднее ехать на машине,  4950 рублей.

               б) выгоднее ехать на поезде,   4530 рублей.

III. Выводы  по итогам решения задач

 Учитель:

- Скажите, решая повседневные задачи вместе с членами этой семьи,  мы хоть раз задумывались, какая профессия у мамы или у папы, какой  профессией овладевает Аня, кем в будущем хочет стать Витя?

Ученики:

- Нет.

Учитель:

-Так какой вывод можно сделать?

Ученики:

-В повседневной жизни любой человек, любой профессии решает математические задачи. Он ходит в магазин, рассчитывает свой бюджет, оплачивает счета, выбирает тариф интернета, телефонной сети, рассчитывает выгодные покупки, планирует, участвует  в ремонте, строительстве, берет кредит и т.д. и т.п.)

Учитель:

-Ребята, вы молодцы.

Давайте подведем итоги:

Хочется закончить наш урок словами известного  древнегреческого философа Платона и великого русского математика М.В. Ломоносова.

Слайд:  

-Разве ты не заметил, что способный к математике изощрен    во всех науках?    (Платон)

-Математику уже затем учить надо, что она ум в порядок приводит.   (М.В. Ломоносов)

Сколько лет прошло, а эти слова в наше время по-прежнему точны и актуальны.

V. Рефлексия.

Ученикам предложено ответить на вопросы по итогам урока (коротко, 1-2 предложения; письменно)

Вопросник:

- Вам понравился урок?                     (Да, нет, почему?)

 (жизненные задачи, познавательные)

На оставшихся же уроках школьники экспериментальной группы будут задействованы в решении практико-ориентированных задач, также практико-ориентированные задачи будут даваться им на домашнее задание. Фрагменты уроков и домашних заданий описаны в Приложении 2.

2.4. Оценка эффективности проведенной работы

Цель контрольного этапа – оценить динамику изменения уровня функциональной грамотности  школьников за счет использования в обучении практико-ориентированных задач.

Задачи контрольного этапа:

1)                провести повторную диагностику уровня функциональной грамотности школьников контрольной и экспериментальной групп;

2)                сравнить результаты диагностики учебной мотивации школьников контрольной и экспериментальной групп на констатирующем и контрольном этапе;

3)                определить эффективность практико-ориентированных задач для развития функциональной грамотности школьников на основе динамики изменения уровня функциональной грамотности школьников.

Для повторной диагностики уровня функциональной грамотности использовалась аналогичная методика (Приложение 3), которая позволяет выявить следующие уровни функциональной грамотности  школьников:

Первый уровень – высокий уровень функциональной грамотности.

Второй уровень – уровень функциональной грамотности выше среднего.

Третий уровень – средний уровень функциональной грамотности.

Четвертый уровень – низкий уровень функциональной грамотности.

Результаты диагностики уровня функциональной грамотности школьников контрольной и экспериментальной групп на контрольном этапе представлены в таблице 2 и на рисунке 2.

                                                                                                           Таблица 2

Результаты диагностики уровня функциональной грамотности школьников контрольной и экспериментальной групп на констатирующем этапе

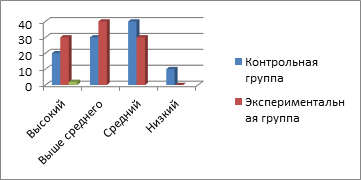
Рис. 2. Результаты диагностики уровня функциональной грамотности школьников контрольной и экспериментальной групп на констатирующем этапе

Вывод:

Сравним результаты диагностики уровня функциональной грамотности школьников контрольной и экспериментальной групп на констатирующем и контрольном этапах исследования, представив эти результаты в таблице 3 и на рисунке 3.

Таблица 3

Сравнительные результаты определения уровня функциональной грамотности школьников контрольной и экспериментальной групп на констатирующем и контрольном этапах исследования

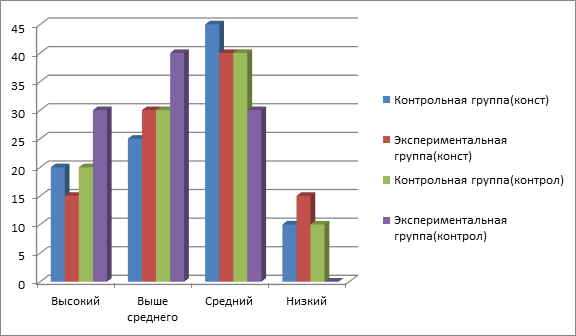
Рис. 3. Сравнительные результаты определения уровня функциональной грамотности школьников контрольной и экспериментальной групп на констатирующем и контрольном этапах исследования

Выводы по II главе

Во второй главе описаны результаты экспериментального исследования, целью которого стало выявление эффективности решения практико-ориентированных задач для развития функциональной грамотности  школьников.

Базой экспериментального исследования явилось Муниципальное бюджетное образовательное учреждение «Быстроистокская общеобразовательная средняя школа» (МБОУ «БОСШ») Алтайского края. В эксперименте принимали участие  школьники – ученики седьмых классов: по 20 школьников в контрольной и экспериментальной группах.

В ходе экспериментального исследования была организована внеурочная деятельность учеников экспериментальной группы.

По результатам экспериментального исследования было выявлено, что решение практико-ориентированных задач играет положительную роль в развитии функциональной грамотности школьников, о чем свидетельствует динамика изменения уровня функциональной грамотности испытуемых экспериментальной группы на протяжении экспериментального исследования.

Заключение

Проведенное исследование позволило достигнуть цели и решить все поставленные задачи.  Изучение теоретических основ развития учебной функциональной грамотности  школьников посредством решения практико-ориентированных позволило сделать следующие выводы:

Практико-ориентированные задачи - это задачи из окружающей действительности, связанные с формированием практических навыков, необходимых в повседневной жизни, в том числе с использованием материалов краеведения, элементов производственных процессов, порою решение одной такой задачи в группе занимает 15-20 минут (в зависимости от мобильности класса и вычислительного объема задачи).

Цель этих задач – формирование умений действовать в социально-значимой ситуации. Они базируются на знаниях и умениях, но требуют умения применять накопленные знания в практической деятельности.

Назначение практико-ориентированных задач – “окунуть” ученика в решение “жизненной” задачи. Важными отличительными особенностями практико-ориентированных задач от стандартных математических (предметных, межпредметных, прикладных) являются: o значимость (познавательная, профессиональная, общекультурная, социальная) получаемого результата, что обеспечивает познавательную мотивацию учащегося; o условие задачи сформулировано как сюжет, ситуация или проблема, для разрешения которой необходимо использовать знания из разных разделов основного предмета – математики, из другого предмета или из жизни, на которые нет явного указания в тексте задачи; o информация и данные в задаче могут быть представлены в различной форме (рисунок, таблица, схема, диаграмма, график и т.д.), что потребует распознавания объектов; o наличии избыточных, недостающих или противоречивых данных в условии задачи, что приводит к объемной формулировке условия; o наличии нескольких способов решения (различная степень рациональности), причем данные способы могут быть неизвестны учащимся, и их потребуется сконструировать.

Перед учителем математики стоит нелёгкая задача – преодолеть в сознании обучающихся представление о «сухости», формальном характере, оторванности этой науки от жизни и практики, обеспечить органическую связь изучаемого теоретического материала с его практической значимостью.

Обучение с использованием практико-ориентированных заданий приводит к более прочному усвоению информации, так как возникают ассоциации с конкретными действиями и событиями. Особенность этих заданий (необычная формулировка, связь с жизнью, межпредметные связи) вызывают повышенный интерес учащихся, способствуют развитию любознательности, творческой активности. Школьников захватывает сам процесс поиска путей решения задач. Они получают возможность развивать логическое и ассоциативное мышление.

Наполнение учебных материалов, задачами, приближенными к жизни требует, с одной стороны, содержательной разработки таких задач, с другой – создание специальных методик работы с ними.

Систематическая работа по решению и конструированию  практико-ориентированных задач и использование разнообразных приёмов    обеспечивает стабильные результаты учебной деятельности по предмету.

Список использованной литературы

1.                PISA 2018 Assessment and Analytical Framework. - Paris: OECD Publishing, 2019. - URL: https://www.oecd.org/education/pisa-2018-assessment-and-analytical-framework-b25efab8-en.htm (дата обращения: 25.05.2022).

2.                Азимов, Э. Г. Новый словарь методических терминов и понятий : (теория и практика обучения языкам) / Э. Г. Азимов, А. Н. Щукин. - М. : Икар, 2009. - 448 с.

3.                Балл, Г. А. О психологическом содержании понятия «задача» / Г. А. Балл // Вопросы психологии : шестнадцатый год издания / Ред. А. А. Смирнов, О. А. Конопкин. – 1970. – №6 ноябрь-декабрь 1970. – С. 75-86.

4.                Бермус, А. Г. Проблемы и перспективы реализации компетентностного подхода в образовании / А. Г. Бермус / Интернет-журнал "Эйдос". – 2005. – 10 сентября. – URL: http://www.eidos.ru/journal/2005/0910-12.htm (дата обращения: 25.05.2022).

5.                 Бикеева, А. С. Какие задачи хотелось бы решать в школе (Записки стороннего наблюдателя) / А. С. Бикеева // Математика в школе. - 2013. - № 1. - С. 3-7.

6.                 Болтянский, В. Г. Математическая культура и эстетика / В. Г. Болтянский // Математика в школе. – 1982. – № 2. – С. 40-43.

7.                 Большой энциклопедический словарь : [В 2 т.] / под ред. А. М. Прохоров. – 2-е изд., перераб. и доп. – М. : Сов. энцикл., 1991. – 862 с.

8.                 Виноградова, Л. В. Методика преподавания математики в средней школе : учебное пособие / Л. В. Виноградова. - Ростов н/Д. : Феникс, 2015. – 252 с.

9.                Волкова, В. Ф. Реализация практико-ориентированного образования на уроках математики / В. Ф. Волкова / Молодой ученый. – 2014. – № 11.1. – С. 32-33. - URL: https://moluch.ru/archive/70/12030/ (дата обращения: 25.05.2022).

10.            Егупова, М. В. Использование практических задач в обучении геометрии / М. В. Егупова // Математика в школе. - 2011. - № 10. - С. 39-44.

11.            Захарова, О. А. Научим ли мы плавать без воды? / О. А. Захарова. -  Издательство «Академкнига/Учебник». - URL: www.akademkniga.ru/umk/files/pub9.doc (дата обращения: 29.05.2022).

12.            Курганов, С. Ю. Ключевые учебные ситуации и тестирование / С. Ю. Курганов // Школьные технологии. - 2006. - № 4. - С. 97-102.

13.            Мордкович, А. Г. Алгебра. 7 класс. В 2 частях. Часть 2. : Задачник для учащихся общеобразовательных учреждений / А. Г. Мордкович [и др.] ; под редакцией А. Г. Мордковича. — 17-е издание, стер. — М. : Мнемозина, 2013. — 217 с.

14.             Мордкович, А. Г. Алгебра. 8 класс. В 2 частях. Часть 2. : Задачник для учащихся общеобразовательных учреждений / А. Г. Мордкович [и др.] ; под редакцией А. Г. Мордковича. — 11-е издание, исправлено и дополнено — М. : Мнемозина, 2013. — 344 с.

15.            Образовательная система «Школа 2100». Педагогика здравого смысла : сборник материалов в помощь учителям, администрации школ и ДОУ, работникам органов управления образованием, методистам, преподавателям ИПК, педколледжей и педвузов, студентам педагогических учебных заведений / под ред. А. А. Леонтьева. - М. : Баласс, 2003. – 367 с.

16.            ОГЭ 2022. Математика : 40 тренировочных вариантов по новой демоверсии 2022 года : учебно-методическое пособие / под ред. Ф. Ф. Лысенко. – Ростов-на-Дону : Легион, 2021. – 384 с.

17.             ОГЭ 2022. Математика : Типовые экзаменационные варианты : 36 вариантов / под ред. И. В. Ященко. – М. : Национальное образование, 2022. – 224 с.

18.            Печёнкина, Е. Н. Практико-ориентированные задачи на уроках математики в основной школе / Е. Н. Печёнкина. - URL: http://rudocs.exdat.com/docs/index-100680.html (дата обращения: 30.05.2022).

19.            Поварушкина, Н. В. Практико-ориентированное обучение на уроках математики в условиях реализации программы профильной школы / Н. В.  Поварушкина. - URL: http://festival.1september.ru/articles/501094/ (дата обращения: 30.05.2022).

20.            Приютко, О. Н. Практико-ориентированные задачи в контексте изменения программ школьного курса математики : Практико-ориентированные задачи в контексте изменения программ школьного курса математики  / О. Н. Приютко, В. И. Берник. – URL: http://Matem/praktiko-orientzadachi/izmen/progr/matematika (дата обращения: 30.05.2022).  

21.            Сборник нормативных документов. Математика / сост. Э. Д. Днепров, А. Г.Аркадьев. - М. : Дрофа, 2007. - 128 с.

22.            СДАМ ГИА : РЕШУ ОГЭ : сайт. - URL:  https://math-oge.sdamgia.ru/test?theme=103 (дата обращения: 30.05.2022).  

23.            Сластенин, В. А. Педагогика : учеб. пособие для студ. высш. пед. учеб. заведений / В. А. Сластенин, И. Ф. Исаев, Е. Н. Шиянов ; Под ред. В. А. Сластенина. - М. : Издательский центр "Академия", 2009. - 576 с.

24.            Смирнова, И. М. Задачи с практическим содержанием как средство формирования геометрических представлений учащихся / И. М. Смирнова, В. А.  Смирнов // - Математика в школе. - 2013. - № 6. - С. 19-25.

25.             Соболев, С. К. Роль и место прикладных задач в обучении математики / С. К. Соболев. – URL: https://kopilkaurokov.ru/matematika/prochee (дата обращения: 30.05.2022).   

26.            Терешин, Н. А. Прикладная направленность школьного курса математики : Книга для учителя / Н. А. Терешин. - М. : Просвещение, 2016. — 96 с.

27.            Федеральный государственный образовательный стандарт основного общего образования (утверждено приказом Министерства образования и науки РФ от 17 декабря 2010 г. № 1897).

28.            ФИПИ : сайт. - URL:  http://fipi.ru/ (дата обращения: 30.05.2022).   

29.            Функциональная грамотность младшего школьника: книга для учителя / Н. Ф. Виноградовой, Е. Э. Кочурова, М. И. Кузнецова [и др.]. - М. : Вентана-Граф, 2018. - 288 с.

30.            Шапиро, И. М. Использование задач с практическим содержанием в преподавании математики: Книга для учителя / И. М. Шапиро - М. : Просвещение, 2015. — 96 с.

31.            Ябурова, Е. А. Задачи с практическим содержанием как средство реализации практико-ориентированного обучения математике : специальность 13.00.02 — теория и методика обучения и воспитания (физика, уровень общего образования) : диссертация на соискание ученой степени кандидата педагогических наук / Е. А. Ябурова. – Екатеринбург, 2006. - URL:  http://www.dissercat.com/content/zadachi-s-prakticheskim-soderzhaniem-kak-sredstvo-realizatsii-praktiko-orientirovannogo-obuc (дата обращения: 29.05.2022).   

32.            Ялалов, Ф. Г. Деятельностно-компетентностный подход к практико-ориентированному образованию / Ф. Г. Ялалов. - Интернет-журнал "Эйдос". - 2007. – URL: http://www.eidos.ru/journal/2007/0115-2.htm (дата обращения: 30.05.2022).    

Приложение 1

Первичная диагностика уровня функциональной грамотности

МИНИСТЕРСТВО ПРОСВЕЩЕНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ

ИНСТИТУТ СТРАТЕГИИ РАЗВИТИЯ ОБРАЗОВАНИЯ РОССИЙСКОЙ АКАДЕМИИ ОБРАЗОВАНИЯ

Диагностическая работа для учащихся 7 классов

МАТЕМАТИЧЕСКАЯ ГРАМОТНОСТЬ

ИНСТРУКЦИЯ для УЧАЩИХСЯ

Работа состоит из четырех заданий, каждое задание описывает одну ситуацию. В каждом задании два вопроса. Таким образом, всего в работе 8 вопросов, на которые вам необходимо будет дать ответ.

На выполнение работы отводится 40 минут.

Внимательно читайте описание ситуации, вчитывайтесь в условие, рассматривайте иллюстрации.

Обращайте внимание на то, в какой форме требуется дать ответ.

При ответе на вопрос с выбором ответа нужно указать все варианты ответа, которые вы считаете верными, поставив знак «√».

При ответе на вопрос с кратким ответом записывайте ответ в специально отведенном месте после слова «Ответ».

В работе есть вопросы, к которым нужно не только дать ответ, но и записать обоснование, привести решение. В этих случаях написано:

«Запишите ответ и приведите соответствующее обоснование», указано место для ответа и для вашего решения.

Задания выполняйте последовательно. Если не удаётся сразу найти ответ на поставленный вопрос, пропустите его и переходите к следующему. Если останется время, вы сможете вернуться к пропущенным заданиям или отдельным вопросам.

И не забывайте делать проверку полученного ответа.

Желаем успеха!

Задание 1. «Тормозной путь». Тормозным путём называется расстояние, которое прошло транспортное средство от момента нажатия на педаль тормоза до полной остановки. При движении автомобиля его тормозной путь зависит от его скорости, а также от состояния дорожного полотна, которое зависит от погодных условий.

Вопрос 1/2. Сотрудник дорожно-патрульной службы проводит занятие с водителями, нарушившими на дороге скоростной режим. Он просит их, используя данные представленные на диаграмме, выбрать в таблице верные утверждения.

Какие утверждения являются верными? Поставьте V.

Вопрос 2/2. На занятиях с будущими водителями изучается, от каких параметров зависит тормозной путь автомобиля.

Для   расчёта   ориентировочной  длины    тормозного   пути    легкового автомобиля на практике используют формулу:

v2

S = 254 × k

, где

S – тормозной путь (в метрах),

v – скорость автомобиля в момент начала торможения (в км/ч),

k – коэффициент сцепления шин с дорогой.

Эта формула удобна тем, что скорость в ней подставляется в км/ч, а длина выражается в метрах.

Значения k – коэффициента сцепления шин с дорогой приведены в таблице:

Автомобиль, двигавшийся по мокрой дороге со скоростью 60 км/ч, начал торможение.

Вычислите его тормозной путь, результат округлите до целого.

Ответ:                                                                                                               

Задание 2. «Поездки на метро». В кассе метрополитена продают билеты на различное количество поездок (см. таблицу).

Билеты на одну и на две поездки действуют 5 дней с момента продажи (включая день продажи). Билеты на 20, 40, 60 поездок действуют 90 дней с момента продажи.

Вопрос 1/2. Лиза ездит на занятия в колледж на метро, поэтому купила билет на 40 поездок. Но поскольку Лиза заболела и не могла ездить на занятия некоторое время, она успела совершить только 36 поездок.

С учётом этого обстоятельства оправдала ли себя покупка билета на 40 поездок по сравнению с покупкой одноразовых билетов?

Запишите ответ и приведите соответствующее обоснование.

Ответ:                                                                                                               

Обоснование:                                                                                                   

Вопрос 2/2. Мама Лизы работает 5 дней в неделю и пользуется для поездки на работу и обратно метрополитеном. В другие дни она не пользуется метрополитеном.

Выгодно ли ей покупать билет на 60 поездок?

Запишите ответ и приведите соответствующее обоснование.

Ответ:                                                                                                               

Обоснование:                                                                                                   

Задание 3. «Бугельные подъемники». Для подъёма горнолыжников и сноубордистов к месту начала спуска используют различные типы горнолыжных подъёмников: гондольные, кресельные и бугельные

Бугельные подъёмники осуществляют подъём лыжников от нижней станции до верхней за счёт бугеля (перекладины) или тарелки, их вместимость – 1 или 2 человека.

Характеристики двух бугельных подъёмников представлены в таблице.

Вопрос 1/2. На рисунке изображён график зависимости расстояния между бугелем и нижней станцией подъемника от времени движения.

По горизонтальной оси отложено время движения бугеля (в минутах), по вертикальной оси – расстояние от бугеля до нижней станции (в метрах).

Посмотрите на график и ответьте на вопросы:

А) Какое расстояние будет между бугелем и нижней станцией через 3 минуты после начала подъёма?

Ответ:                                                                 

Б) Для какого подъёмника (А или Б) представлен график зависимости? Ответ:                                                                             

Вопрос 2/2. Пропускная способность подъёмника – это количество лыжников, которые могут подняться от нижней станции до верхней в течение одного часа.

Что необходимо знать из приведённого ниже списка, чтобы подсчитать пропускную способность подъёмника? Поставьте V:

Задание 4. «Покупка телевизора». Телевизоры различаются не только моделями, но и длиной диагонали экрана. Традиционно диагональ экрана измеряют в дюймах: 1 дюйм ≈ 2,54 см.

Вопрос 1/2. Семья Петровых решила купить телевизор и повесить его в гостиной в нише круглой формы. Диаметр ниши равен 1,6 м.

В магазине им предложили современные безрамочные телевизоры с диагоналями экранов: 50, 55, 60, 65, 70, 80, 85, 90 и 100 дюймов.

Из предложенных в магазине вариантов выберите телевизор, имеющий наибольшее значение диагонали экрана, подходящее Петровым.

Запишите ответ.

Ответ:                                                                                                               

Вопрос 2/2. Семья Ивановых решила купить телевизор и повесить его на кухне в нише шкафа. Размер ниши: ширина – 80 см, высота – 60 см.

Сможет ли семья Ивановых разместить в нише широкоформатный телевизор с диагональю экрана 37 дюймов, если его высота равна 18 дюймам?

Запишите ответ и приведите соответствующее обоснование.

Ответ:                                                                                                               

Обоснование:                                                                                                   

Приложение 2

Фрагменты уроков 7 класса, с использованием практико-ориентированных задач

Урок по геометрии: «Повторение. Параллельные прямые»

Задача 1:

Школьная клумба имеет форму ромба со стороной 4 м и острым углом 30 градусов.

Определите количество рассады астры, которой необходимо для необходимо для посадки на этой клумбе, если на 1м 2 требуется 30 штук, процент «приживаемости» цветов астры – 96%.

Задача 2:

Определите количество парковых роз, которые можно всадить на школьной клумбе, имеющей форму прямоугольника со сторонами 3м и 5м, если на 3 м 2 высаживается 5 роз.

Задача на домашнюю работу:

Пруд имеет форму квадрата, в углах которого растут дубы. Как увеличить площадь квадрата вдвое, чтобы не пострадали дубы?

Урок по алгебре: «Решение задач с помощью систем уравнений: метод подстановки»

Задача 1:

 Мать старше дочери на 23 года, а вместе им 51 год. Сколько лет дочери?

Задача 2:

Девять лет назад брат был вдвое старше сестры. Сколько лет брату и сколько сестре, если брат старше сестры на 4 года?

Задача 3:

 Двое рабочих за 5 часов могут сделать 115 деталей. Если первый рабочий будет работать 3 часа, а второй 4 часа, то они сделают вместе 81 деталь. Сколько деталей сделает каждый из них за час?

Задача 4:

 Сумма двух положительных чисел равна 120, причем первое число составляет 40% второго. Найдите эти числа.

Задача на домашнюю работу:

 Сумма двух чисел 180, частное от деления числа на второе равно 5. Найдите эти числа.

Урок по алгебре: «Решение задач с помощью систем уравнений: комбинация различных приемов»

Задача 1:

В трех сосудах 48 л воды. Если из первого сосуда перелить во второй 3 л, то воды в этих двух сосудах будет поровну, а если из третьего сосуда перелить во второй 3 л, то в третьем воды окажется в 7 раз меньше, чем во втором. Сколько воды в каждом сосуде?

Задача 2:

Периметр треугольника равен 3 дм. Наибольшая из сторон на 4 см больше наименьшей; а удвоенная третья сторона равна сумме двух других сторон. Найдите стороны треугольника.

Задача на домашнюю работу:

На ферме содержатся коровы, овцы, козы. Всего 1328 животных. Коров на 120 меньше, чем овец, и на 100 больше, чем коз. Сколько животных каждого вида на ферме?

Приложение 3

Повторная  диагностика уровня функциональной грамотности

Контрольное исследование

Диагностическая работа для учащихся 7 классов

МАТЕМАТИЧЕСКАЯ ГРАМОТНОСТЬ

ИНСТРУКЦИЯ для УЧАЩИХСЯ

Работа состоит из 1 задания, который описывают одну ситуацию. Каждое задание содержит 4 вопроса, на которые вам необходимо будет дать ответ.

На выполнение работы отводится 35 минут.

Внимательно читайте описание ситуации, вчитывайтесь в условие, рассматривайте иллюстрации.

Обращайте внимание на то, в какой форме требуется дать ответ. При ответе на вопрос с выбором ответа нужно указать все варианты ответа, которые вы считаете верными, поставив знак « √ ».

При ответе на вопрос с кратким ответом записывайте ответ в специально отведенном месте после слова «Ответ».

В работе есть вопросы, к которым нужно не только дать ответ, но и записать обоснование, привести решение.

В этих случаях написано: «Запишите ответ и приведите соответствующее обоснование», указано место для ответа и для вашего решения.

Отвечайте на вопросы последовательно. Если не удаётся сразу найти ответ на поставленный вопрос, пропустите его и переходите к следующему.

Если останется время, вы сможете вернуться к пропущенным заданиям или отдельным вопросам.

И не забывайте делать проверку полученного ответа.

Желаем успеха!

Задание 1. «Покупка квартиры». Семья Петровых купила квартиру в новостройке.

Квартира состоит из двух комнат, кухни и коридора и санузла (см. план). Кухни имеет размеры 3,5 м на 3,5 м первая комната 3,5 м на 4,5 м, санузел имеет размеры 2 м на 1,5 м, длина коридора 10,5 м.

Вопрос 1. Изучите план-схему квартиры и выберите верное утверждение:

КРИТЕРИИ ОЦЕНИВАНИЯ (0 ИЛИ 1 БАЛЛ):

Вопрос 2. Найдите площадь 2-ой комнаты в квадратных метрах. Ответ представьте в виде числа без наименования единиц измерения.

КРИТЕРИИ ОЦЕНИВАНИЯ (0 ИЛИ 2 БАЛЛА):

Вопрос 3.

Расположите в порядке возрастания площади всех комнат квартиры, указанных в план-схеме. Ответ представьте в виде чисел без наименования единиц измерения, записав их через запятую.

Найдите общую площадь всей квартиры (в квадратных метрах). Ответ представьте в виде числа без наименования единиц измерения

КРИТЕРИИ ОЦЕНИВАНИЯ (0, 1, 2 ИЛИ 3 БАЛЛА):

Вопрос 4 . Владельцы квартиры планируют обновить пол в коридоре новой плиткой.

Изучите представленные в таблице условия трех поставщиков.

Какой поставщик предоставил самый выгодный вариант, с учетом демонтажа старой плитки?

Во сколько рублей обойдется владельцам самый выгодный вариант. Запишите ответ и приведите соответствующее обоснование.

Скачано с www.znanio.ru