Решение проектных задач на уроках геометрии в средней школе

Решение проектных задач на уроках геометрии в средней школе

Математика как учебный предмет играет важную роль в формировании личности. Ведущей целью математического образования является интеллектуальное развитие личности, формирование качеств мышления, необходимых для социализации человека. Для ориентации в современном мире каждому человеку необходим набор знаний и умений математического характера.   

  Главной стратегией современной школы является системное формирование универсальных учебных действий, обеспечивающих «умение учиться», возможность каждого стремиться к саморазвитию и самосовершенствованию путем осознанного и активного овладения новым социальным опытом, а не только усвоение обучающимися конкретных предметных знаний и умений в рамках отдельных дисциплин. При этом приобретенные знания, умения и навыки формируются, сохраняются и применяются в тесной связи с активными действиями самих учащихся.

  Развивает и формирует ученика не только само знание, сколько метод его приобретения. Если учебная деятельность протекает только в рамках воспроизведения усвоенных знаний, то это не способствует развитию человека.

Основная проблема, которая возникает передо мной, когда я приступаю к работе в новом классе – низкий уровень познавательной активности из-за отсутствия учебной мотивации, неумения учащихся ориентироваться в нестандартных условиях, применять знания на практике, переносить математические знания в смежные области.

На протяжении всей педагогической деятельности я искала пути и способы повышения мотивации учащихся к изучению математики, привлекая их к самостоятельному приобретению знаний. 

Для повышения мотивации к изучению математики на своих уроках я часто использую проектные задачи, в основе которых находится реальная жизненная проблемная ситуация, анализ которой позволяет учащимся самостоятельно ставить перед собой цели, правильно формулировать задачи и разрабатывать план действий.

При решении проектных задач ученик ищет, доказывает, рассуждает, ошибается, убеждается в своих ошибках и снова ищет пути решения задачи, и, наконец, решает её. Такой процесс решения развивает, обогащает мысль ученика, вырабатывает навыки самостоятельности в познании нового.

Пример проектной задачи: Бак, имеющий форму прямоугольного параллелепипеда с квадратным основанием, должен вмещать 500 литров воды. При какой стороне основания площадь поверхности бака (без крышки) будет наименьшей?

Данная проектная задача может быть предложена учащимся 10-11 классов по алгебре и началам математического анализа в рамках изучения темы «Задачи на отыскание наибольших и наименьших значений величин». 

Цели решения задачи: 

Общеобразовательные: углубление понимания сущности производной путём применения её для получения новых знаний; установление межпредметных связей.

Развивающие: формирование умений строить доказательство, логическую цепочку рассуждений; формирование умений проводить обобщение, переносить знания в новую ситуацию.

Воспитательные: воспитание познавательного интереса к учебному предмету; воспитание у учащихся культуры логического мышления. 

Основополагающий вопрос: Какой должна быть сторона основания, чтобы бак имел наименьшую поверхность.

Учебные вопросы: 

•      Площадь квадрата.

•      Площадь прямоугольника.

•      Площадь поверхности прямоугольного параллелепипеда.

•      Объём прямоугольного параллелепипеда.

•      Возрастание и убывание функции.

•      Точки максимума и минимума.

•      Область определения функции.

•      Наименьшее и наибольшее значение функции на промежутке.

Этапы работы над задачей:

Первый этап: Составление математической модели (перевод задачи на язык функций. Для этого выбирается удобный параметр , через который интересующая нас величина выражается как функция ).

1)      Проанализировав условие задачи, выяснить оптимизируемую величину (О.В.), т.е. величину, о наименьшем значении которой идёт речь. Обозначить её буквой S.

2)      Одну из участвующих в задаче неизвестных величин, через которую сравнительно нетрудно выразить О.В., принять за независимую переменную (Н.П.) и обозначит её буквой . Установить реальные границы изменения Н.П. (в соответствии с условием задачи), т.е. область определения для искомой О.В.

3)      Исходя из условия задачи, выразить S через . Математическая модель задачи представляет собой функцию  с областью определения Х, которую нашли на втором шаге.

Второй этап: Работа с составленной моделью (средствами анализа отыскать наименьшее значение функции на промежутке).

На этом этапе для функции  найти , используя при этом правила нахождения наибольшего и наименьшего значений непрерывной функции на промежутке.

Третий этап: Ответ на вопрос задачи (интерпретация найденного решения, т.е. «перевод» его с языка функций в терминах задачи).

На данном этапе следует дать конкретный ответ на вопрос задачи, опираясь на результаты, полученные на этапе работы с моделью.

Решение задачи: Первый этап. Составление математической модели.

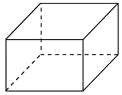
1)      О.В. – площадь поверхности бака, т.к. в задаче требуется выяснить, когда эта площадь будет наименьшей. Обозначим О.В. буквой S.

2)      Площадь поверхности зависит от измерений прямоугольного параллелепипеда. Сторону квадрата, служащего основанием бака, примем за Н.П. и обозначим её буквой . По смыслу задачи

3)      Если бак вмещает 500 л воды, то объём V бака равен 500   . Если h – высота бака,

        то               , откуда

 и 4-х прямоугоьников со

сторонами  и       . Значит,

Второй этап: Работа с составленной моделью. 

Задача сводится к отысканию наименьшего значения функции , где

.

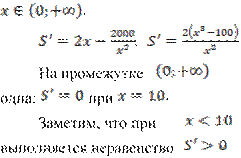 критических точек нет, а стационарная точка только

 выполняется неравенство , а при  

. Значит,  – единственная стационарная точка,

причём точка минимума функции на заданном промежутке, а потому в этой точке функция принимает наименьшее значение.

Третий этап: Ответ на вопрос задачи.

В задаче спрашивается, какой должна быть сторона основания, чтобы бак имел наименьшую поверхность. Мы выяснили, что сторона квадрата, служащего основанием такого бака, равна 10 дм.

Ответ: 10 дм.