Практическая работа №4

Тема: Решение задач линейного программирования симплекс- методом

Цель: - решить задачу линейного программирования тремя способами: 1) графическим методом; 2) симплекс – методом; 3) при помощи средства «Поиск решения» в Microsoft Excel.

Вид работы: фронтальный

Время выполнения: 2 часа

Задания к практической работе

·  Графический способ решения задач линейного программирования в случае 2 независимых переменных (хотя возможно решение в случае 3 переменных). Алгоритм решения задач: 1) изобразить область, соответствующую системе неравенств 2) если целевая функция имеет вид: f(x₁,x₂)=c₁x₁+c₂x₂, то очевидно: . Следовательно, вектор градиента имеет вид: grad(f)=(c₁,c₂). На плоскости изобразить вектор градиента и перпендикулярную ему линию уровня функции f 3) для нахождения максимума функции f требуется перемещать линию уровня параллельным переносом в направлении вектора градиента. Для нахождения минимума линию уровня следует перемещать в направлении противоположном градиенту. Перемещение линии уровня продолжать до тех пор, пока она имеет общие точки с областью допустимых решений 4) при достижении «крайнего положения» перемещение прекратить, зафиксировать полученный ответ.  В зависимости от конкретной задачи ответом может служить: одна точка; все точки некоторого отрезка; бесконечно удаленная точка.

·  Симплекс-метод. Идея метода заключается в следующем: в качестве начального приближения рассматривается координата некоторой вершины многогранника допустимых решений. Требуется найти все ребра, исходящие из этой вершины. Путем движения вдоль ребра, по которому целевая функция убывает, придем в новую вершину. Далее требуется найти все ребра, выходящие из полученной вершины и продолжить процедуру. После конечного числа шагов придем в такую вершину, движение из которой невозможно, т.к. вдоль всех ребер, выходящих из этой вершины целевая функция возрастает. Координаты полученной вершины являются решением задачи.

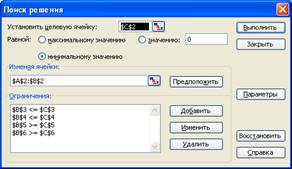
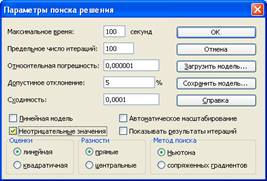
Способ поиска максимума или минимума функции помощи средства «Поиск решения» в Microsoft Excel основывается на встроенных функциональных возможностях программы Microsoft Excel. Краткий алгоритм: 1) в меню «Сервис» в разделе «Надстройки» необходимо активизировать функцию «поиск решения» 2) выделить область листа размером 2х2, в ячейки этой области будут занесены результаты решения, а именно координаты точки максимума или минимума,  соответственно 3) в соседних клетках ввести значения, которые лежат в левой и правой частях неравенств 4) в отдельной таблице размера 1х2 запишем значение целевой функции 5) вызвать средство «поиск решения», в качестве целевой ячейки выбрать ту, в которой хранится значение целевой функции, выбрать вариант максимум или минимум, в окне «изменяя ячейки» указать ячейки, содержащие x₁ и x₂, добавить каждое из ограничений, указав в виде ссылки ячейку левой части неравенства и правой части, выставив между ними требуемый знак 6) в параметрах установить неотрицательные значения 7) нажав на кнопку «выполнить», получить результат.

Ход работы

Найти максимум и минимум функции  при заданных ограничениях:

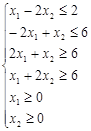
Решить задачу линейного программирования тремя способами:

·           симплекс-методом

·           графическим методом

·           средством «Поиск решения» в программе Microsoft Excel

1.     Решим поставленную задачу графическим методом.

Изобразим область допустимых решений, соответствующую системе ограничений-неравенств.

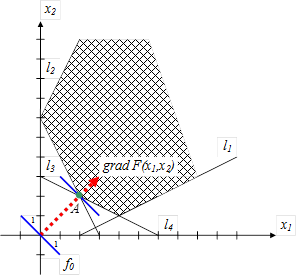
Найдем градиент функции :

На плоскости переменных  и  изобразим вектор-градиент  и перпендикулярную ему линию уровня . Перемещая линию уровня вдоль вектора-градиента, мы придем в бесконечность, т.е. . Таким образом, исследуемая функция не имеет точки максимума. Перемещая линию уровня в направлении антиградиента , получим «точку выхода» с координатами A(2;2). При этом исследуемая функция принимает свое минимальное значение равное

2.     Решим поставленную задачу симплекс-методом.

Найдем минимум исследуемой функции.

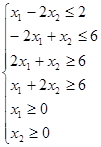
Так как симплекс-метод разработан для задач линейного программирования в канонической форме, то требуется перейти от ограничений-неравенств к ограничениям-равенствам путем введения балансовых переменных.

                     (1)

Из системы уравнений (1) видно, что в качестве свободных переменных проще всего выбрать . Тогда базисные переменные  выражаются через свободные так:

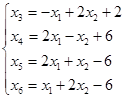                       (2)

Если положить все свободные переменные равные нулю, то, используя систему уравнений (2), получим базисное решение:

Это базисное решение является недопустимым, так как не выполняются условия:

Пусть . Тогда из системы уравнений (2) следует, что:

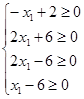
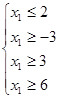
Используя систему уравнений (2) найдем базисное решение с учетом :

Так как свободными переменными стали  и , то необходимо «переразрешить» систему уравнений (2), а именно выразить переменную , ставшей базисной, через переменные ,  и подставить полученное выражение в оставшиеся уравнения системы:

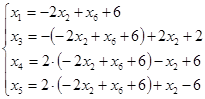
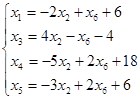            (3)

Этому набору свободных и базисных переменных соответствует базисное решение:

Значение целевой функции при данном базисном решении:

Найденное базисное решение является недопустимым, поскольку не выполняется условие

В выражении целевой функции , которая выражена через свободные переменные  и , коэффициент при  отрицателен. Значит, увеличивая , можно уменьшить значение целевой функции .

Пусть . Тогда из системы уравнений (3) следует, что:

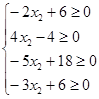
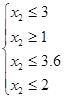
Используя систему уравнений (3) найдем базисное решение с учетом :

Так как свободными переменными стали  и , то необходимо «переразрешить» систему уравнений (3), а именно выразить переменную , ставшей базисной, через переменные ,  и подставить полученное выражение в оставшиеся уравнения системы:

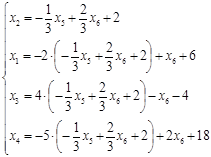
               (4)

Этому набору свободных и базисных переменных соответствует базисное решение:

Значение целевой функции при данном базисном решении:

Найденное базисное решение является допустимым, поскольку .

В выражении целевой функции коэффициенты при свободных переменных  и  неотрицательны. Значит, найденное базисное решение является оптимальным, т.е. решение  доставляет минимум целевой функции , значение которого равно 12.

Найдем максимум исследуемой функции.

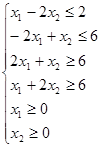
Для того чтобы применить симплекс-метод необходимо перейти от задачи максимизации к эквивалентной задаче минимизации и от ограничений-неравенств к ограничениям-равенствам. Задача, удовлетворяющая указанным требованиям и эквивалентная исходной, будет выглядеть следующим образом:

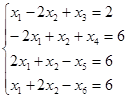            (5)

Из системы уравнений (5) видно, что в качестве свободных переменных проще всего выбрать . Тогда базисные переменные  выражаются через свободные так:

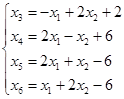             (6)

Если положить все свободные переменные равные нулю, то, используя систему уравнений (6), получим базисное решение:

Это базисное решение является недопустимым, так как не выполняются условия:

Пусть . Тогда из системы уравнений (6) следует, что:

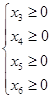
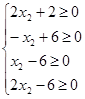
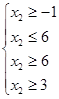                         (7)

Используя систему уравнений (6) найдем базисное решение с учетом :

Так как свободными переменными стали , и , то необходимо «переразрешить» систему уравнений (6), а именно выразить переменную , ставшей базисной, через переменные ,,и подставить полученное выражение в оставшиеся уравнения системы:

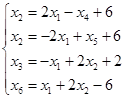
В полученной системе уравнений имеются два выражения для базисной переменной . Так как ограничивающим неравенством в системе неравенств (7) является неравенство , соответствующее неравенству , то из двух выражений для базисной переменной  следует выбрать выражение :

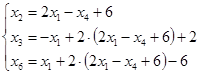
         (8)

Этому набору свободных и базисных переменных соответствует базисное решение:

Значение целевой функции при данном базисном решении:

Найденное базисное решение является допустимым, поскольку .

В выражении целевой функции , которая выражена через свободные переменные  и , коэффициент при  отрицателен. Значит, увеличивая , можно уменьшить значение целевой функции .

Пусть . Тогда из системы уравнений (8) следует, что:

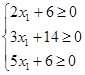
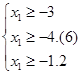                (9)

Из системы неравенств (9) видно, что свободная переменная  неограниченна сверху. Это значит, что ее значение можно увеличивать до бесконечности. При этом минимальное значение целевой функции  равно . Возвращаясь к первоначальной задаче, делаем вывод, что исследуемая функция  не имеет точки максимума.

3.     Решим поставленную задачу с помощью средства «Поиск решения» в программе Microsoft Excel.

Структура листа в Microsoft Excel.

Найдем минимум исследуемой функции :

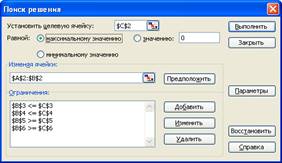
Найдем максимум исследуемой функции :

Так как графический и симплекс-методы показали, что исследуемая целевая функция  не имеет максимума, то можно сделать вывод, что полученный результат является неверным и был получен в результате достижения предельного значения представления чисел в Microsoft Excel.

Контрольные вопросы

1.     Как решается задача графическим методом?

2.     Как решается задача симплекс-методом?

3.     Как решается задача с помощью средств «Поиск решения»?

4.     Зачем перепроверяют решение задачи разными методами?

Скачано с www.znanio.ru