Решение задач по математическим методам в экономике

Практическое задание в Excel

Решение задач по математическим методам в экономике

 (файл .xls  можно скачать на странице  www.matburo.ru/sub_appear.php?p=l_excel ) 

Задача 1.

Три станка обрабатывают два вида деталей – А и В. Каждая деталь проходит обработку на всех трех станках. Известны: время обработки каждой детали на каждом станке и время работы станков в течение одного цикла производства.

Цена одной детали А – 4000 руб., В – 6000 руб.

Составить план производства деталей А и В, обеспечивающий максимальный доход по цеху.

 Также определить, как повлияет на решение: а) снижение цены детали В до 5000 руб.; б) снижение времени работы третьего станка до 21 ч за один цикл производства; в) возрастание цены детали В на 4000 руб.

Решение.

Составляем модель в Excel.

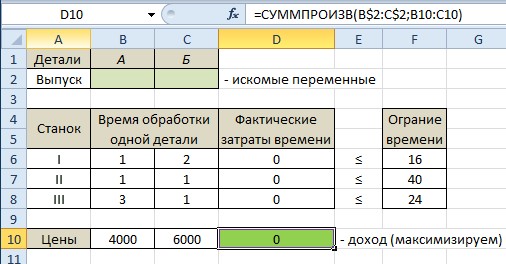
Настраиваем Поиск решения.

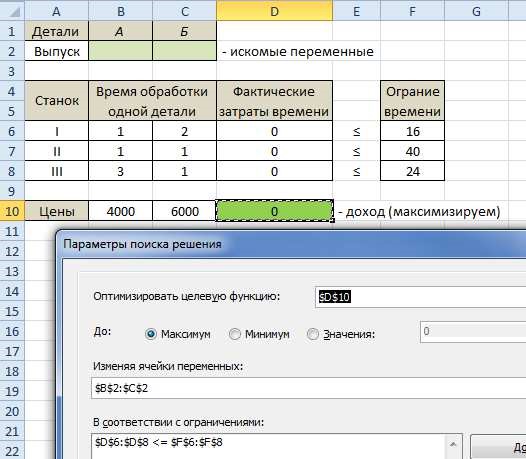
Получаем.

Необходимо выпускать 6,4 детали А и 4,8 детали Б, максимальный доход – 54400 руб.

Решение получилось не в целых числах.

Для получения решения в целых числах добавляем ограничение целочисленности.

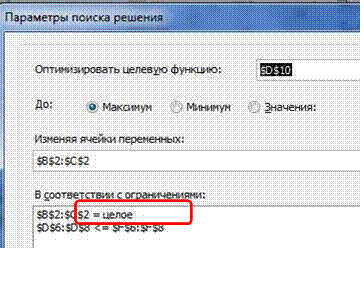
Получаем.

Необходимо выпускать 6 деталей А и 5 деталей Б, максимальный доход – 54000 руб.

Определить, как повлияет на решение: 

а) снижение цены детали В до 5000 руб.; 

Структура производства не меняется, только снижается доход до 49000 руб.

б) снижение времени работы третьего станка до 21 ч за один цикл производства; 

Необходимо выпускать 4 детали А и 6 деталей Б, максимальный доход – 52000 руб.

в) возрастание цены детали В на 4000 руб.

Необходимо выпускать 8 деталей Б, максимальный доход – 80000 руб.

Задача 2.

На строительство четырех объектов (1,2,3,4) кирпич поступает с трех (I, II, III) заводов. Заводы имеют на складах соответственно 50, 100 и 50 тыс. шт. кирпича. Объекты требуют соответственно 50, 70, 40, 40 тыс. шт. кирпича. Тарифы (д.е./ тыс. шт) приведены в следующей таблице:

Составьте план перевозок, минимизирующий суммарные транспортные расходы.

Решение.

Составляем модель в Excel.

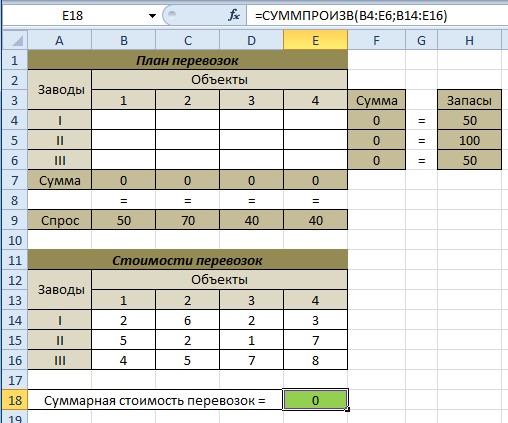
Настраиваем Поиск решения.

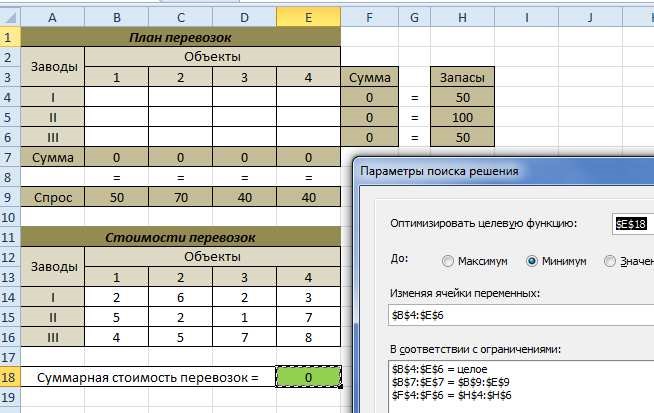
Получаем.

Минимальная стоимость перевозок = 510.

Задача 3

Дана платежная матрица Р игры с природой. 

−20 10 6 

                              

Р= 10 8 2  

−12 7 3 

                              

 18 5 19

Известный вероятности наступления событий П природы и равны (02 054 026,    ,      ,      ) .

Найти оптимальное поведение игрока для максимизации среднеожидаемого выигрыша.

Решение.

Пусть переменные – вектор-столбец вероятностей выбора игроком стратегий:

(p p p p1            2                 3          4)T 

Тогда ожидаемый выигрыш игрока:

                                               −20 10 6                                     

                                                                                                  

( p1        p2         p3         p4)⋅−10 8 212 7 3 ⋅(02 054 026,  ,  ,           )Т 

                                                                                                  

                                                18 5 19                                    

Составляем модель в Excel.

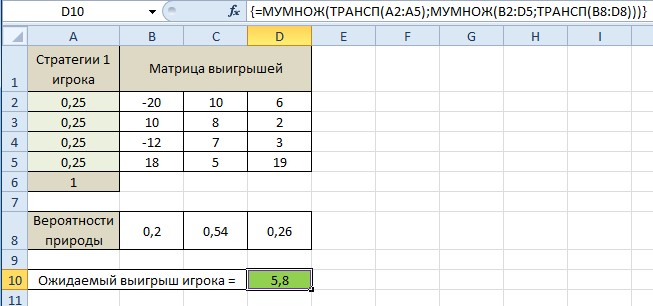
В данной модели выборы стратегий равновероятны и равны 0,25.

Единственное ограничение – сумма вероятностей = 1.

Настраиваем Поиск решения.

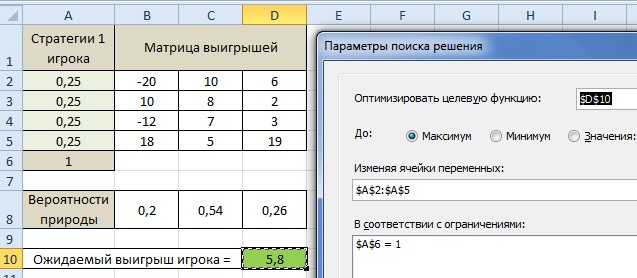
Получаем.

Надо однозначно выбирать 4-ю стратегию, максимальный ожидаемый выигрыш = 11,24.

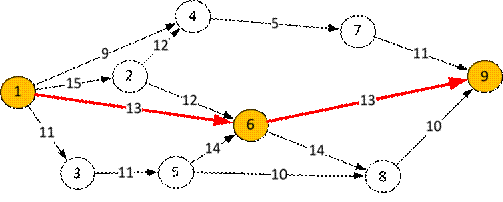
Задача 4

Для сетевой модели:

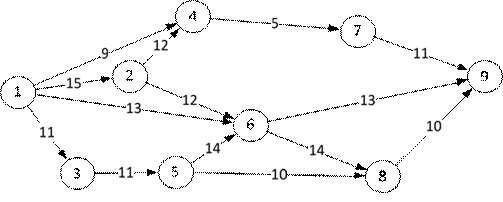
определить критический путь.

Решение.

Составляем матрицу смежности графа (взвешенную).

Убираем 1 столбец и 9 строку.

По отсутствующим направлениям ставим очень большие значения, например, 1000.

Далее составляем матрицу переменных:

Переменные – наличие дуги между вершинами (то есть 1 или 0).

Находим суммы по строкам и столбцам.

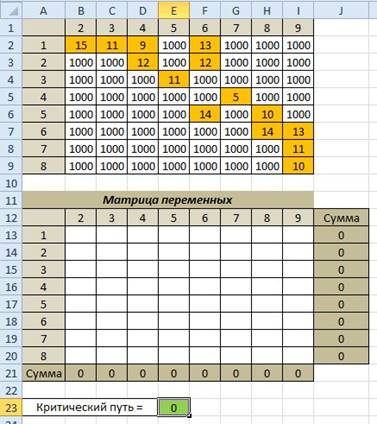
Находим критический путь – умножаем поэлементно матрицу смежности и матрицу переменных (СУММПРОИЗВ())

Теперь составляем задачу.

Необходимо минимизировать критический путь с ограничениями:

1.  выходим из вершины 1 – сумма по строке 1 = 1

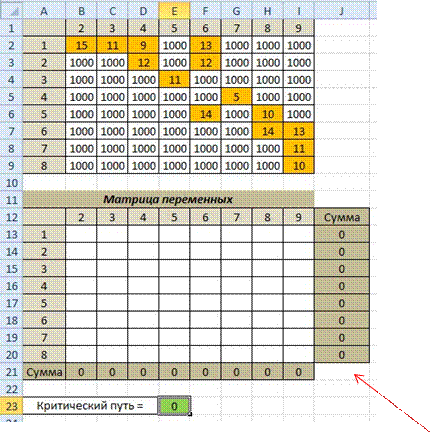
2.  входим в вершину 9: сумма по столбцу 9 = 1

3.  если мы вошли в вершину, то должны оттуда выйти: сумма в строке для каждой вершины не может быть меньше суммы по столбцу.

Настраиваем Поиск решения.

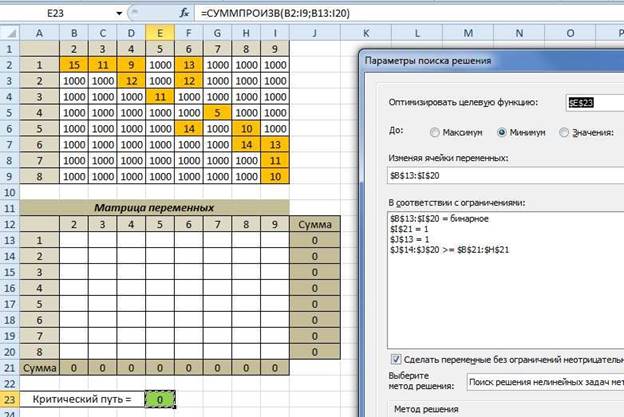
Получаем.

Критический путь = 26, дуги пути: (1,6), (6,9).

На графе.