Решение задачи о раскрое стержней

ЗАДАНИЕ.  

Завод заключил договор на поставку комплектов стержней

длиной 18, 23 и 32 см. Причём количество стержней разной длины в комплекте должно быть в соотношении 1:5:3. на сегодняшний день имеется 80 стержней длиной 89 см. Как их следует разрезать, чтобы количество комплектов было максимальным? Какова при этом будет величина отходов?

                           РЕШЕНИЕ.          

Составляем математическую модель раскроя с учётом

комплектации и ограничением на используемый материал.

Определяем все рациональные способы раскроя материала (т.е.

стержней длиной 89 см) на заготовки типа А (стержни длиной 32 см), типа B (стержни длиной 23 см) и типа C (стержни длиной 18 см). Таких способов оказывается девять.

Обозначим 

x₁ – количество стержней, раскраиваемых по 1-му варианту,  x₂ – количество стержней, раскраиваемых по 2-му варианту, x₃ –  количество стержней, раскраиваемых по 3-му варианту, x₄ – количество стержней, раскраиваемых по 4-му варианту,  x₅ – количество стержней, раскраиваемых по 5-му варианту, x₆ –  количество стержней, раскраиваемых по 6-му варианту, x₇ – количество стержней, раскраиваемых по 7-му варианту,  x₈ – количество стержней, раскраиваемых по 8-му варианту, x₉ –  количество стержней, раскраиваемых по 9-му варианту, N – количество комплектов.

Общее количество раскраиваемых стержней не должно превышать

имеющееся количество, т.е. 80.  Следовательно, имеем первое ограничение: 

x₁+ x₂+ x₃ + x₄+ x₅+ x₆ + x₇ + x₈ + x₉≤ 80.

Общее количество всех заготовок А, полученное при раскрое равно 

2x₁+2x₂+ x₃ + x₄+ x₅. 

Общее количество всех заготовок В, полученное при раскрое равно 

x₁+ 2x₃ + x₄+ 3x₆ +2x₇ + x₈. 

Общее количество всех заготовок С, полученное при раскрое равно 

x₂ + x₄ + 3x₅ + x₆ + 2x₇ + 3x₈ + 4x₉. 

  Т.к. число комплектов равно N и в каждом комплекте должно быть 1 заготовка С, 5 заготовок B и 3 заготовки А, то всего должно быть не менее N заготовок С, 5N заготовок В и 3N заготовок А, т.е. 

2x₁+2x₂+ x₃ + x₄+ x₅ ≥ 3N ; x₁+ 2x₃ + x₄+ 3x₆ +2x₇ + x₈≥ 5N; x₂ + x₄ + 3x₅ + x₆ + 2x₇ + 3x₈ + 4x₉≥ N.

В задаче требуется найти максимальное значение целого числа  N.

Математическая модель задачи имеет вид: Найти max N     при следующих ограничениях: 2x₁ + 2x₂ + + + −x₃ x₄ x₅ 3N ≥ 0



                          x₁ + 2x₃ + +x₄  3x₆ + 2x₇ + −x₈ 5N ≥ 0       



                           x₂ + +x₄  3x₅ + +x₆  2x₇ +3x₈ + 4x₉ − N ≥ 0

                                         x₁ + + + + + + + +x₂    x₃             x₄            x₅           x₆           x₇           x₈           x₉ ≤ 80

и при выполнении условий  ^x_i ≥ 0,  N≥ 0,   ^x_i −_целые.

Решаем задачу в EXCEL с использованием модуля «Поиск

решения».

Введённые значения и формулы

Полученное решение

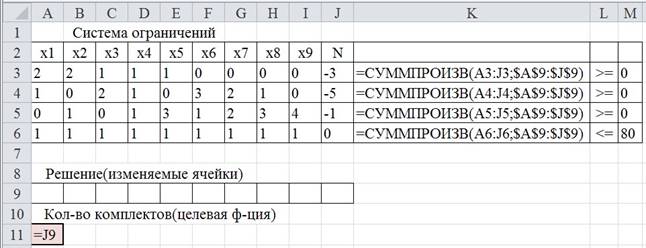
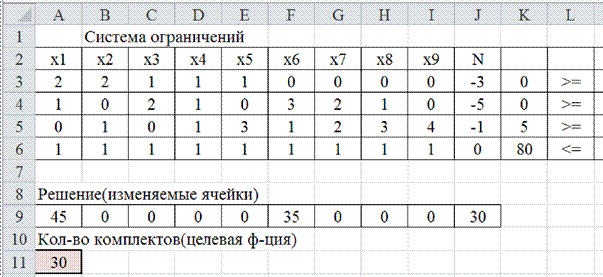Из полученного решения видно, что для получения оптимального

раскроя необходимо разрезать 45 стержней по варианту 1, т.е. из каждого из 45-и стержней длиной 89 см получить 2 стержня по 32 см и 1 стержень 23 см, и 35 стержней разрезать по варианту раскроя 6, т.е. из каждого из этих 35-и стержней длиной 89 см получить 3 стержня по 23 см длиной и 1 стержень длиной 18 см.

Таким образом, мы получим из 80-и стержней длиной 89 см 2×45 = 90 стержней длиной 32 см, 1×45+3×35=150 стержней длиной 23 см и 1×35=35 стержней длиной 18 см. Из этого набора можно образовать N=30 полных наборов и 5 стержней длиной 18 см останутся лишними.

Подсчитаем величину отходов при таком плане. 

Каждый разрез стержня по 1-му варианту даёт 2 см отходов. Следовательно, из 45-и разрезанных по 1-му варианту стержней мы получим 90 см отходов.

Каждый разрез стержня по 6-му варианту даёт тоже 2 см отходов. Следовательно, из 35-и разрезанных по 6-му варианту стержней мы получим ещё 70 см отходов.

Если оставшиеся неукомплектованными 5 стержней длиной 18 см

тоже считать отходами, то это добавляет ещё 5×18 = 90 см отходов.

Итого получаем 90+70+90 = 250 см отходов.