Решение задачи по теории принятия решений

Решение 

ЗАДАНИЕ.  

Для откорма скота на ферме используют 3 вида прикормки. При правильном откорме необходимо удовлетворять минимальные требования по потреблению трех основных пищевых ингредиентов (углеводы, протеины и витамины). Содержание каждого ингредиента в 1 кг каждого вида корма, минимальные нормы потребления ингредиентов, а также цена 1 кг каждого вида корма приведены в таблице

Задания:

1)                Построить математическую модель задачи минимизации издержек (записать переменные, целевую функцию и ограничения).

2)                Найти дневной рацион откорма, минимизирующий издержки, и величину минимальных издержек.

3)                Все ли виды корма вошли в рацион? Какой должна быть цена за 1 кг корма, не вошедшего в рацион, чтобы он туда вошел? Для ответа на данный вопрос использовать отчет об устойчивости.

4)                Что приведет к большему снижению издержек – уменьшение на 5 единиц дневной нормы потребления углеводов или уменьшение дневной нормы потребления протеинов

5)                Приведет ли к снижению издержек уменьшение дневной нормы потребления витаминов? Для ответа на данный вопрос использовать отчет об устойчивости.

РЕШЕНИЕ.  

1) вводим переменные x₁ – количество корма А x₂ – количество корма В x₃ – количество корма С

Модель задачи

F =84x₁ +72x₂ +60x₃ → min

90x₁ +20x₂ +40x₃ ≥200 

30x₁ +80x₂ +60x₃ ≥180            



10x₁ +20x₂ +60x₃ ≥150 x ,x ,x1 2 3 ≥0

2)  решаем задачу в Excel заносим данные

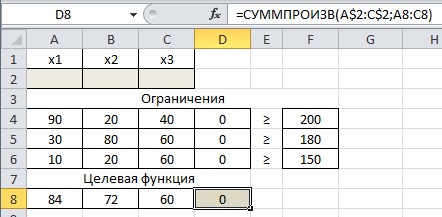
Настраиваем Поиск решения

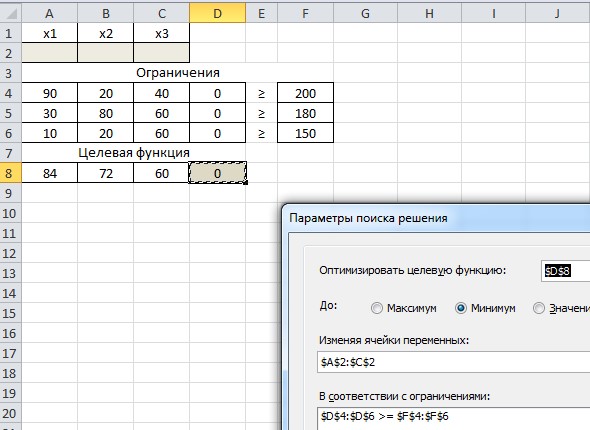
Получаем.

3)  Анализируем решение.

В рацион входит 1,143 ед. корма А и 2,429 ед. корма С, корм В в рацион не входит.

Смотрим отчет по устойчивости.

Ячейки переменных

                                         Окончательное Приведенн. Целевая функция Допустимое        Допустимое

        Ячейка Имя          Значение           Стоимость         Коэффициент         Увеличение Уменьшение

Ограничения

Нам нужен столбец Тень цена, в котором находятся двойственные оценки. Для нахождения цены корма В умножаем двойственны оценки на расход корма В:

0,771*20+0,486*80+0*20=54,286 руб.

То есть, чтобы корм В вошел в рацион, его цена должна быть не выше 54,286 руб.

4)                уменьшение на 5 единиц дневной нормы потребления углеводов приведет к снижению издержек на 5*0,771 = 3,857 руб. уменьшение на 5 единиц дневной нормы потребления протеинов приведет к снижению издержек на 5*0,486 = 2,429 руб.

то есть снижение нормы потребления углеводов приводит к большему снижению издержек

5)                уменьшение дневной нормы потребления витаминов не приводит к снижению издержек, так как двойственная оценка равна 0