Решение заданий № 17 варианта КИМ ЕГЭ по математике профильного уровня

Задание № 17 варианта КИМ ЕГЭ по математике профильного уровня

Подготовила : учитель МОУ СОШ п. Прудовой Екатериновского района Саратовской области. 2020 г.

Текстовая задача с экономическим содержанием – относительно новый вид заданий, появившихся в КИМ ЕГЭ профильного уровня, хотя задачи «на проценты» в вариантах вступительных экзаменов в вузы встречались в «доегэшную пору» достаточно часто, особенно если речь шла об экономических специальностях.

Решение таких задач связано со знанием некоторых специфических математических моделей из области экономики, умением переводить сформулированные в виде текста условия в уравнения и неравенства и пониманием того, как решения полученных уравнений и неравенств соотносятся с тем, что написано в условии задачи, – то есть какой смысл имеют полученные результаты.

         С чего начать подготовку к решению экономической задачи? Прежде всего, стоит вспомнить основные правила решения текстовых задач вообще (они пригодятся и для решения более простой текстовой задачи № 11 варианта КИМ).

Решение любой текстовой задачи складывается из нескольких основных моментов:

• чтение условия задачи; читайте его до тех пор, покуда сможете, не подглядывая в текст, объяснять суть описанного в задаче процесса (без конкретных числовых данных, конечно, – зазубривать ничего не нужно);

•    выбор переменных; для каждого типа задач существуют рекомендации, какие величины лучше всего обозначать как переменные (и это не всегда те величины, о которых идет речь в вопросе задачи); переменных при решении текстовой задачи нужно вводить столько, сколько их нужно для того, чтобы просто и логично составить уравнения и неравенства (не бойтесь, если переменных оказалось слишком много – например, больше, чем число уравнений: если вы все делаете правильно, то «лишние» переменные взаимно уничтожатся или сократятся;еще один вариант – в процессе решения надо будет найти не сами переменные по отдельности, а какую-либо их комбинацию);

• составление уравнений и неравенств, формализация того, что необходимо найти в процессе решения задачи; при составлении уравнений обращайте внимание на единицы измерения – они должны быть одинаковыми для всех одноименных величин;

• решение полученного уравнения, неравенства или системы;

• исследование полученного результата и нахождение ответа на вопрос задачи.

Рекомендуем вам «держать в голове» эти основные шаги решения текстовой задачи.

Если все эти правила вам хорошо знакомы и текстовые задачи вы решаете, в принципе, неплохо, то есть умеете составлять математические модели словесно описанных процессов, то дальше нужно выяснить, насколько хорошо вы владеете таким понятием как «процент». Для этого можно решить следующую устную задачку: «Цена на товар была повышена на 25%. На сколько процентов надо теперь ее снизить, чтобы получить первоначальную цену?»

«Очевидный» (и неправильный) ответ – на столько же, хотя на самом деле снизить надо на 20%.

Если приведенная выше задачка не загнала вас в тупик, то, немного потренировавшись в вычислении «простых» процентов, можно переходить к освоению формулы «сложных процентов» и ее применению в задачах с экономическим содержанием. Следующий этап – решение задач на банковские вклады, ведь такие задачи уже можно встретить в вариантах КИМ ЕГЭ.

Например: «Вклад в размере 10 млн рублей планируется открыть на четыре года. В конце каждого года банк увеличивает вклад на 10% по сравнению с его размером в начале года. Кроме этого, в начале третьего и четвёртого годов вкладчик ежегодно пополняет вклад на х млн рублей, где х — целое число. Найдите наименьшее значение х, при котором банк за четыре года начислит на вклад больше 7 млн. рублей». (Ответ: 8.)

Сравнительно недавно в вариантах КИМ появились задачи, темой которых являются банковские кредиты. Для решения таких задач необходимо познакомиться с двумя математическими моделями, лежащими в основе наиболее распространенных схем выплат по банковскому кредиту, – дифференцированной и аннуитетной. В основе этих схем лежит уже известная нам формула «сложных» процентов, а также свойства арифметической и геометрической прогрессий. Поэтому прежде чем начинать знакомиться с «кредитной» математикой необходимо повторить некоторые свойства уже упомянутых прогрессий – вам понадобятся определения, формулы n-го члена и суммы  n последовательных членов каждой из прогрессий.

При решении задач, в которых речь идет о выплате кредита в соответствии с дифференцированной или аннуитетной схемой, можно действовать двумя способами: либо использовать готовые формулы, полученные в ходе построения соответствующей математической модели, либо вычислять размер очередного платежа пошагово. Выбор способа зависит от условия задачи. Конечно, есть и еще некоторые хитрости в построении решения, которые надо знать.

К наиболее сложным задачам с экономическим содержанием относятся так называемые «задачи на оптимизацию» или экстремальные задачи. Эти задачи описывают разнообразные ситуации, с которыми граждане, предприятия и компании могут встретиться в своей экономической деятельности. К решению таких задач есть несколько подходов, из которых наиболее часто используются метод перебора вариантов и логических рассуждений и исследование функций элементарными методами и с помощью производной.

Как правило, при решении данных задач необходимо либо провести непосредственные вычисления и сравнить их результаты, либо составить уравнение (систему уравнений) и решить его (ее) с учетом некоторых дополнительных условий (например, в целых числах), либо построить функцию, устанавливающую связь между двумя экономическими величинами (например, между объемом производства и прибылью компании), и исследовать ее на экстремальное значение с помощью производной, опять же с учетом того, что данная функций описывает некий реальный процесс, от чего могут зависеть какие-то ограничения на область определения или область значений.

Задачи на оптимизацию – это уже настоящие исследовательские задачи, очень близкие по смыслу (но не по методам решения) к следующей по сложности задаче вариантов КИМ ЕГЭ – задаче с параметром.

Например, на пробном экзамене в 2020 году предлагалась следующая непростая задача: «Страховой фонд владеет акциями, стоимость которых равна t2

тыс. рублей в конце каждого года  t (t=1, 2, …)

. Фонд может продать все акции в конце каждого года и положить все вырученные от продажи средства на счет в банке. Известно, что тогда в конце каждого следующего года банк будет увеличивать сумму, находящуюся на счете, в r раз, где r – некоторое положительное число больше единицы. Оказалось, что если фонд продаст все акции и вложит деньги в банк именно в конце 21-го года, то в конце 25-го года он получит наибольшую из возможных прибыль. Определите, какие при этом значения может принимать число r».

РАСЧЕТ БАНКОВСКИХ КРЕДИТОВ. ВЫВОД ФОРМУЛ.

В этом разделе будут рассмотрены задачи на вычисления связанные с кредитованием, а именно нахождение: процентной ставки, суммы долга, суммы переплаты, ежегодных (ежемесячных, еженедельных т.д.)  выплат, количество лет. Данные подсчеты экономически целесообразны в связи с тем, что каждый человек при заключении договора определяет наиболее выгодные для себя условия.

Такие задания классифицируются на простые, решения которых ограничиваются одной формулой, и сложные решение которых требует составления систем, решение неравенств и т.д. 

Для многих задач данного типа удобно использовать формулы, выведение которых представлено ниже.

Рассмотрим основные элементы, которые встречаются в задачах, и дадим им характеристику:

•       S – сумма, которую берут в кредит

•       r – годовая/месячная ставка

•       k – число, показывающее во сколько раз увеличивается сума S перед банком  (k = 1+0,01*r)

•       x - выплата

•       n – количество лет/месяцев, за которое необходимо выплатить кредит

•       F – сумма, которую в итоге придется вернуть банк

•      P – переплата, равная F - S

4.1. Вывод формул для решения задач на равные размеры выплат.

Первая формула на нахождение суммы долга, обычно в задачах условия кредитования следующие: в банке берется кредит и увеличивается на r процентов, затем вносится выплата, и сумма оставшегося долга увеличивается на r процентов, и так через n лет происходит погашение кредита.

Задача1. [6] В июле планируется взять кредит на сумму 6 409 000 рублей. Условия его возврата таковы:

 - каждый январь долг возрастает на 12,5% по сравнению с концом предыдущего года;

 - с февраля по июнь каждого года необходимо выплатить некоторую часть долга.

Сколько рублей нужно платить ежегодно, чтобы кредит был полностью погашен двумя равными платежами (то есть за два года)?

Решение.

1.      Составим краткую запись:

S = 6 409 000 рублей

r = 12, 5%                k = 1+0,01r = 1,125 =

х = ? рублей

n = 2 года

2. 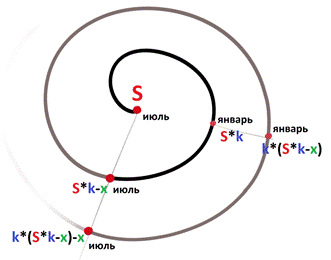     Проиллюстрируем процесс кредитования на спирали:

 

 

 

 

 

 

 

 

Заметим, что кредитование похоже на цикл, в котором можно выделить три этапа: долг перед банком, выплата, остаток. Перенесем все данные в таблицу.

3.      Перенесем данные в таблицу:

Долг (S*k)	Выплата	Остаток
Sk	x	Sk-x
k(Sk-x)	x	k(Sk-x)-x

 

Долг (S*k)	Выплата	Остаток
6 409 000 *	x	6 409 000 *-x
* (6 409 000 *-x)	x	* (6 409 000 *-x) - x

4.      Составим уравнение, где последний остаток равен нулю, чтобы узнать размер выплаты

* (6 409 000 *-x) – x = 0

6 409 000 * - х – х = 0

- х = -

 x = *

x = 3 817 125 (рублей)

Ответ: 3 817 125 рублей

Рассмотрим вторую задачу такого же типа.

Задача 2. [6]  В июле планируется взять кредит в банке на некоторую сумму. Условия его возврата таковы:

 - каждый январь долг возрастает на 20% по сравнению с концом предыдущего года;

- с февраля по июнь каждого года необходимо выплатить часть долга, равную 2,16 млн рублей

 Сколько млн рублей было взято в банке, если известно, что он был полностью погашен тремя равными платежами (то есть за три года)?

Решение.

Так же запишем краткую запись:

S = ? млн рублей

r = 20%

k = 1, 2

x = 2, 16 млн рублей

n = 3 года

Долг (Sk)	Выплата	Остаток
Sk	x	Sk-x
k(Sk-x)	x	k(Sk-x)-x
k(k(Sk-x)-x)	x	k(k(Sk-x)-x)-x

Раскроем скобки

Долг (Sk)	Выплата	Остаток
Sk	x	Sk-x
Sk2-kx	x	Sk2-kx - x
Sk3-k2x - kx	x	Sk3-k2x - kx - x

Sk³-k²x - kx – x = 0

Sk³ =k²x + kx + x

Sk³  = х (k²+ k + 1) (сделаем замену числа k)

S*1, 2³  =х (1,2²+ 1,2 + 1) (сделаем замену числа х)

S = 

S =

S = 4, 55 (млн рублей)

Ответ: 4,55 млн рублей

Заметим, что обе задачи решаем по одной схеме. Различия в том, что в первой задаче ищем размер выплат, а во второй задаче – сумму, взятую в кредит. В обеих задачах приходим к одной формуле.

Задача 1.  k(Sk-x)-x=0(последний остаток равен 0) , отсюда

                                                   

 

С этого момента можем получить две формулы.

1.               2. 

Задача 2.    (последний остаток равен 0) , отсюда

                                                   

 

С этого момента можем получить две формулы.

1.               2. 

Задача 3. [5]  31 декабря 2014 года Алексей взял в банке 9 282 рублей в кредит под 10% годовых. Схема выплаты кредита следующая: 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на 10%), затем Алексей переводит в банк X рублей. Какой должна быть сумма X, чтобы Алексей выплатил долг четырьмя равными платежами (то есть за четыре года)

Решение. Снова нарисуем спираль.

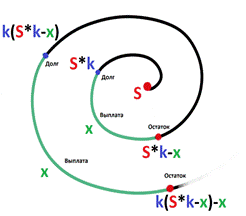
Решение.

Краткая запись:

S = 9 282 000 млн

 r = 10% (годовые)

 k = 1+0,01r = 1 + 0,01*10 =1,1

 n = 4 года

 х =? рублей

Долг(S*k)	Выплата	Остаток
Sk	х	Sk - x
k(kS-x)	x	K(kS-x) - x
k(k(kS-x) - x)	x	K(K(kS-x) - x) - x
K(K(K(kS-x) - x) - x)	x	K(K(K(kS-x) - x) - x) - x

 Раскроем скобки

Долг(S*k)	Выплата	Остаток
Sk	х	Sk - x
k2S-kx	x	k2S-kx - x
k3S-k2x- kx	x	k3S-k2x - kx - x
k4S-k3x – k2x - kx	x	k4S-k3x - k2x - kx-x

*Примечание: на основании этой таблицы, можно вывести формулу

KⁿS – k^n-1x – k^n-2x – k^n-3x - …. - kx –x = 0

Составим уравнение, где последний остаток равен нулю.

 k⁴S-k³x - k²x - kx-x = 0 (подставим вместо k число  )

()⁴S = x(()³ + ()² +  + 1)

()⁴S = x (+  +  + 1)

 ()⁴S = x

 11⁴*S÷10⁴ = 4641x÷10³

4641x*10⁴ = 11⁴S*10³

x = 11⁴S*10³ ÷ 4641*10⁴   (заменим S на 9 282 000)

 12

x = 14 641 * 9 282 000 ÷ 4641

x = 2 928 200

Ответ: 2 928 200 рублей

Второй способ решения задачи.

Назовем эти задачи А) Задачи на  равный размер выплат.    

Зная, что мы долг должны погасить четырьмя равными платежами запишем формулу

последнего остатка k⁴S-k³x - k²x - kx-x = 0. Отсюда выведем

k⁴S=k³x + k²x + kx+x .

 ;  Если бы мы искали S, то получили бы формулу ;

На основании решений задач 1, 2, 3 запишем формулы

;                                                              ;

4.2  Решение задач на сокращение остатка на одну долю от целого.

Следующий тип задач назовем тип Б) Задачи на сокращение остатка на одну долю от целого

Пример решения задачи типа Б:

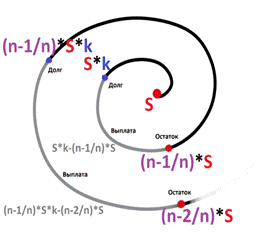
Задача 4. [5]   15 января планируется взять кредит в банке на 24 месяца. Условия его возврата таковы:

 - 1-го числа каждого месяца долг возрастает на 3% по сравнению с концом предыдущего месяца;

 - со 2-го числа пло14-е число каждого месяца необходимо выплатить часть долга;

 - 15-го числа каждого месяца долг должен быть на одну и ту же величину меньше долга на 15-е число предыдущего месяца.

Известно, что в течение первого года кредитования нужно вернуть банке 466,5 тыс. рублей. Какую сумму планируется взять в кредит?

Решение.

Краткая запись:

S =? рублей

r = 3%

k = 1+0,01*3 = 1,03

Сумма x за 12 месяцев = 466,5 тыс. рублей

n = 24 месяца       

С каждым месяцем долг будешь уменьшаться в ,    ….  ,, 0

Долг (S*k)	Выплата	Остаток
Sk	Sk -S= S(k-1)+S	S
Sk	Sk -S =  S(k-1)+S	S
Sk	Sk -S =  S(k-1)+S	S
Sk	Sk - S =S(k-1)+S	S
Sk	Sk -S =S(k-1)+S	S
Sk	Sk -S = S(k-1)+S	S
Sk	Sk -S = S(k-1)+S	S
Sk	Sk - S = S(k-1)+S	S
Sk	Sk -S = S(k-1)+S	S
Sk	Sk -S= S(k-1)+S	S
Sk	Sk - S =S(k-1)+S	S
Sk	Sk - S = S(k-1)+S	S

Составим уравнение, где сумма всех выплат будет равняться всем выплатам за год кредитования. Найдем сумму кредита.

S(k-1)*(1 + + +++++++++) + S = 466 500

S(k-1)* + S = 466 500 (заменим число k на 1,03)

S(1,03-1)* + S = 466 500

S*(0,03* + ) = 466 500

= 466 500

S =

S = 600 000 (рублей)

Ответ: 600 000 рублей

Запишем общую формулу для решения данной задачи.

-сумма выплат

Применим ее для решения следующей задачи.

Задача 5. [3]   15-го января планируется взять кредит в банке на 19 месяцев. Условия его возврата таковы:

 - 1-го числа каждого месяца долг возрастает на r% по сравнению с концом предыдущего месяца;

- со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;

- 15-го числа каждого месяца долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца.

 Известно, что общая сумма выплат после полного погашения кредита на 30% больше суммы, взятой в кредит. Найдите r.

Решение.

.

Подставим в формулу наши данные, получим

Сгруппируем    ;;;;;

;;.

Получим 9 пар по 1. Поэтому

.

   

                                                                                                                  Ответ: 3%

Задача 6. [4]  В июле планируется взять кредит на сумму 18 млн. рублей на некоторый срок(целое число лет). Условия его возврата таковы:

-каждый январь долг возрастает на 10 % по сравнению с концом предыдущего года;

-с февраля по июнь каждого года необходимо выплатить часть долга;

-в июле каждого года долг должен быть на одну и ту же сумму меньше долга на июль предыдущего года.

На сколько лет планируется взять кредит , если известно, что общая сумма после выплат после его погашения составит 27 млн. рублей.

Решение.   Снова обратимся к той же формуле

F-сумма выплаченная банку, P-переплата

 

Подставив в эту формулу найдем

Ответ: 9 лет.

 

Сложность таких задач в том, что здесь нет готовых методов решения, каждая задача уникальна и требует своего подхода. Поэтому посоветовать можно только одно: чтобы научиться решать такие задачи, надо их решать. Впрочем, этот совет – универсальный.

 

 

 

 

 

 

 

 

СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ:

Интернет-источники:

1.Web –Википедия «Процент»https://ru.wikipedia.org/wiki/%D0%9F%D1%80%D0%BE%D1%86%D0%B5%D0%BD%D1%82

2.РЕШУ ЕГЭ Образовательный портал для подготовки к экзаменам/ https://math-ege.sdamgia.ru/?redir=1

3.Самообразование. Главная > 2017: ЕГЭ, ОГЭ Предметы > ЕГЭ 2017. Математика. И.В. Ященко. 36 вариантов. Профильный уровень / http://self-edu.ru/ege2017_36.php

Литературные источники:

4.И.В.Ященко «ЕГЭ-2018 МАТЕМАТИКА ПРОФИЛЬНЫЙ УРОВЕНЬ» - М., Национальное образование, 2018г.

5. И.В.Ященко «ЕГЭ-2017 МАТЕМАТИКА ПРОФИЛЬНЫЙ УРОВЕНЬ» -М. , Национальное образование , 2017г.

6.А.В. Семенов, И.В.Ященко «КАК ПОЛУЧИТЬ МАКСИМАЛЬНЫЙ БАЛЛ НА ЕГЭ МАТЕМАТИКА »-М.,  Интеллект -центр , 2015г.

7.А. Г. Малкова «МАТЕМАТИКА  АВТОРСКИЙ КУРС ПОДГОТОВКИ К ЕГЭ»_ Ростов – на- Дону, Феникс, 2017г.

 

 

Скачано с www.znanio.ru