13   Oscillations

By the end of this topic, you will be able to:

13.1 (a) describe simple examples of free oscillations (b) investigate the motion of an oscillator using experimental and graphical methods

(c) understand and use the terms amplitude, period, frequency, angular frequency and phase difference, and express the period in terms of both frequency and angular frequency

(d) recognise and use the equation a = —c0²x as the defining equation of simple harmonic motion

(e) recall and use x = xo sin as a solution to the equation a = — c0²x

               (O recognise and            the equations v = vo cos cot and

v ± (x0² — x² )

(g) describe, with graphical illustrations, the changes in displacement, velocity and acceleration during

13.2 (a) describe the interchange between kinetic and potential energy during simple harmonic motion

13.3 (a) describe practical examples of damped oscillations with particular reference to the effects of the degree of damping and the importance of critical damping

(b) describe practical examples of forced oscillations

and resonance

(c)
describe graphically how the amplitude of a forced oscillation changes with frequency near the natural frequerry of the system, and understand qualitatively the factors that determi1E the frequency response and tie sharpness of resonance

(d) appreciate that there are some circumstances in which resonance is useful and other circumstances in which resonance should be

complete oscillation

Figure 13.1 Oscillation of a mass on a spring

230

Starting points

•An object that moves to-and-fro continuously is said to be oscillating or vibrating.

•Oscillations occur in many different systems from the very small (e.g. atoms) to the very large (e.g. buildings).

13.1 Oscillations

Some movements involve repetitive to-and-fro motion, such as a pendulum, the beating of a hear-t, the motion of a child on a swing, and the vibrations of a guitar string. Another example would be a mass bouncing up and down on a spring, as illustrated in Figure 13.1. One complete movement from the starting or rest position, up, then down and finally back up to the rest position, is known as an oscillation.

The tine taken for one complete oscillation or vibration is referred to as the period Tof the oscillation.

The oscillations repeat themselves.

The number ofoscillations or vibrations per unit time is the frequencyf

Frequency may be measured in hertz (Hz), where one hertz is one oscillation per second (1 Hz = Is—I). However, frequency may also be measured in min-I, hourⁱ, etc. For example, it would be appropriate to measure the frequency of the tides in h-l.

Since period T is the time for one oscillation then frequencyf= VT

13.1 Oscillations

As the mas oscillates, it moves from its rest or equilibrium pc-Ation.

The distance fran the equilibrium position is knovvn as the displacement.

This is a vector quantity, since the displacement may be on either side of the equilibrium position.

The amplitude (a scalar qt.entity) is the rnaximum displacement

Some oscillations maintain a constant period even when the amplitude of the oscillation changes. Galileo discovered this fact for a pendulum. He timed the swings of an oil lamp in Pisa Cathedral, using his INIse as a measure of time. Oscillators that have a constant time period are called isochronous, and may be made use of in timing devices. For example, in quartz watches the oscillations of a small quartz crystal provide constant time intervals. GalileoS experiment was not precise, and we now know that a pendulum swinging with a large amplitude is                              isochronous.

The quantities period, frequency, displacement and amplitude should be familiar from our study of waves in Topic 14. It should not be a surprise to meet them again, as the idea of oscillations is vital to the undetstanding of waves.

Displacement—time graphs

It is possible to plot displacement—time graphs (see AS Level Topic 14) for oscillators. One experimental method is illustrated in Figure 13.2. A mass on a spring oscillates above a position sensor that is connected to a computer through a datalogging interface, causing a trace to appear on the monitor.

Figure 13.2 Apparatus for plotting displacement—time graphs for a mass on a spring

The graph describing the variation of displacement with time may have different shapes, depending on the oscillating system. For many oscillators the graph is approximately a sine (or cosine) curve. A sinusoidal displacement—time graph is a characteristic of an important type of oscillation called simple harmonic motion (s.h.m). Oscillators which move in sh.m. are called harmonic oscillators We shall analyse simple harmonic motion in some detail, because it successfully describes many oscillating systems, both in real life and in theory. Fortunately, the mathematics of

s.h.m. can be approached through a simple defining equation. The properties of the m«ion can be deduced from the relations between graphs of displacement against time, and velocity against time, which we met in Topic 3.

Simple harmonic motion (s.h.m.)

Simpk harmonic motion is defined as the motion of a particle about a fixed point such

that its acceleration a is proportional to its displacement x from the fixed point, and is directed towards the point

Mathematically, we write this definition as a = —oY-x

Figure 13.4 Graph of the defining equation for simple harmonic motion

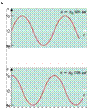
Figure 13.5 Displacement—time curves for the two solutions to the s.h_m. equation

232

where 03² is a constant. We take the constant as a squared quantity, because this will ensure that the constant is always positive (the square of a positive number, or of a negative number, will always be positive). Why worry about keeping the constant positive? This is because the minus sign in the equation must be preserved. It has a special significance, because it tells us that the acceleration a is always in the opposite direction to the displacement x. Remember that both acceleration and displacement are vector quantities, so the minus sign is shorthand for the idea that the acceleration is always directed towards the fixed point from which the displacement is measured. This is illustrated in Figure 13.3.

displacement

point trom

— which displacement is measured

The defining equation is represented in a graph of a against x as a straight line, of negative gradient, through the origin, as shown in Figure 134. The gradient is negative because of the minus sign in the equation. Note that both positive and negative values for the displacement should be considered.

The square root of the constant (that is, 0)) is known as the angular frequency of the oscillation. This angular frequency co is related to the frequency f of the oscillation by the expression

By Newton's second law, the force acting on a body is proportional to the acceleration of the body. The defining equation for simple harmonic motion can thus be related to the force acting on the particle. If the acceleration of the particle is proportional to its displacement from a fixed point, the resultant force acting on the particle is also proportional to the displacement. We can bring in the idea of the direction of the acceleration by specifying that the force is always acting towards the fixed point, or by calling it a restoring force.

Solution of equation for simple harmonic motion

In order to find the displacement—time relation for a particle moving in a simple harmonic motion, we need to solve the equation a = —Ox. To derive the solution requires mathematics which is beyond the requirements of A/AS Physics. However, you need to know the form of the solution. This is

x xo sin or

x = xo cos or

where xo is the amplitude of the oscillation. The solution x = xo sin ax is used when, at time t = O, the particle is at its equilibrium position where x = O. Conversely, if at time t = O the particle is at its maximum displacement, x = xo, the solution is x xo cos ox. The variation with time t of the displacement x for the two solutions is shown in Figure 13-5.

In Topic 3 it was shown that the gradient of a displacement—time graph may be used to determine velocity. Referring to Figure 13-5, it can be seen that, at each time at which x = xo, the gradient of the graph is zero (this applies to both solutions). Thus, the velocity is zero whenever the particle has its maximum displacement. If we think

a)

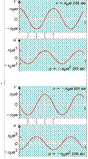
Figure 13.6 Velocity-time and acceleration— time graphs for the two solutions to the s_h.m_ equation

13.1 Oscillations

about a mass vibrating up and down on a spring, this means that when the spring is fully stretched and the mass has its maximum displacement, the mass stops moving downwards and has zero velocity. Also from Figure 13.5, we can see that the gradient of the graph is at a maximum whenever x 0. This means that when the spring is neither under- or over-stretched the speed of the mass is at a maximum. After passing this point, the spring forces the mass to slow down until it changes direction.

If a full analysis is carried out, it is found that the variation of velocity with time is coinusoidal if the sinusoidal displacement solution is taken, and sinusoidal if the cosinusoidal displacement solution is taken. This is illustrated in Figure 13.6. The velocity v of the particle is given by the expressions v = xoocos aN Men x = xo sin (Dt

t,' —XOO sin when X = XO COS

In each                                there is a phase difference between velocity and displacement. The velocity curve is x/2 rad ahead of the displacement curve. (If the phase angle is not considered, the variation with time of the velocity is the same in each case.) The maximum speed vo is given by

There is an alternative expression for the velocity.

        v              (x0² — x²)

which is derived on page 236,

For completeness, Figure 13.6 also shows the variation with time of the acceleration a of the particle. This could be derived from the velocity—time graph by taking the gradient. The equations for the acceleration are a = —xod sin ON when x = xo sin

a = —xod cos ox Lien x xo cos

Note that, for both solutions, these equations are consistent with the defining equation for simple harmonic motion, a = —ex. You can easily prove this by eliminating sin ON from the first set of equations, and cos ON from the second.

The displacementx at time tof a particle moving in simple harmonic motion is given by

0.25 cos 7.5% where x is in metres and t is in seconds.

(a) Use the equation to find the amplitude, frequency and period for the motion. (b) Find the displacement when t = 0.50 s.

(a) Compare the equation with x = xo cos cot. The amplitude xo = 0.25m. The angular frequency 7.5 rad s-1 . Remember that 0) = 21tj; so the frequencyf= c0121t = 7.5/2rt= 1.2 Hz. The period l/f= 1/1.2 = 0.84s.

(b) Substitute t = 0.50s in the equation, remembering that the angle ON is in radians and notdegrees. 7.5 x  215⁰. sox-=0.25 cos 215 ^o =-0.20m.

Now it's your turn

 A mass oscillating on a spring has an amplitude of O. 10m and a period of 2.0s.  Deduce the equation for the displacement x if timing starts at the instant when the mass has its maximum displacement.

 Calculate the time interval from t = O before the displacement is 0.08m.

cose

Figure 13.9 The simple pendulum

Examples of simple harmonic motion

By definition, an object whose acceleration is proportional to the displacement from the equilibrium position, and which is always directed tovmrds the equilibrium pcsition, is undergoing simple harmonic motion. We now look at two simple examples of oscillatory motion which approximate to this definition. They may easily be set up as demonstrations of s.h.m.

Mass on a helical spring

Figure 13.7 illustrates a mass m suspended from a spring. (This sort of spring is called a helical spring because it has the shape of a helix.)

The weight mg of the mass is balanced by the tension Tin the spring. When the spring is extended by an amount Ax, as in Figure 13.8, there is an additional upward force in the spring given by

F = —kAx

where k is a constant for a particular spring, known as the spring constant. The spring constant is a measure of the stiffness of the spring (see Topic 9). A stiff spring has a large value of k; a more flexible spring has a smaller value of and, for the same force, would have a larger extension than one with a large spring constant. The spring constant k is given by the expression

Ax

and is measured in newtons per metre (N In-I).

When the mass is released, the restoring force F pulls the mass towards the equilibrium position. (The minus sign in the expression for F shows the direction of this force.) The restoring force is proportional to the displacement. This means that the acceleration of the mass is proportional to the displacement from the equilibrium position and is directed towards the equilibrium position. This is the condition for simple harmonic motion.

The full theory shows that, for a mass m suspended from a light spring having spring constant k, the period T of the oscillations is given by

For oscillations to be simple harmonic, the spring must obey Hooke's law throughout that is, the extensions must not exceed the limit of proportionality. Furthermore, for large amplitude oscillations, the spring may become slack. Ideally, the spring would have no mass, tuit if the suspended mass is more than about 20 times the mass of the spnng, the error involved in assuming that the spring has no mass is less than 1%.

This example of simple harmonic motion is particularly useful in modelling the vibrations of molecules. A molecule containing two atoms oscillates as if the atoms were connected by a tiny spring The spring constant of this spring depends upon the type of bonding between the atoms. The frequency of oscillation of the molecule can be measured experimentally using spectroscopy, and this gives direct information about the bonding This model can be extended to solids, where atoms are often thought as being ccmnected to their neighbours by springs. Again, this leads to an experimental way of obtaining information about interatomic forces in the solid.

The simple pendulum

Figure 13-9 illustrates a simple pendulum. Ideally, a simple pendulum is a point mass m on a light, inelastic string In real experiments we use a pendulum bob of finite size. When the bob is pulled aside through an angle e and then released, there will be a restoring force acting in the direction of the equilibrium position.

13.2 Energy changes in simple harmonic motion

Because the simple pendulum moves in the arc of a circle, the displacement will be an angular displacement a rather than the linear displacement x we have been using so far.

The two forces on the bob are its weight mg and the tension Tin the string. The component of the weight along the direction of the string, mg cos 9, is equal to the tension in the string. The component of the weight at right angles to the direction of the string mg sin is the restoring force F. This makes the bob accelerate towards the equilibrium position.

The restoring force depends on sin 9 As 9 increases, the restoring force is not proportional to the displacement (in this case e), and so the motion is oscillatory but not simple harmonic. However, the situation is different if the angle 9 is kept small (less than about 5⁰) For these small angles, e is proportional to sin 9. In fact, if 9 is measured in radians, then

9 in radians • sin e

Table 13.1                      You can check this using your calculator. Some values of 0/⁰, e/rad and sin are given in Table 13.1. e

This means that, for small-amplitude oscillations (the angle of the string to the vertical should be less than about 5⁰), the pendulum bob oscillates with simple harmonic motion.

where g is the acceleration of free fall. An experiment in which the period of a simple pendulum is measured can be used to determine the acceleration of free fall. The experiment is repeated for different lengths of pendulum, and the gradient of a graph of T² against I is 4Ʋ/'g This provides an alternative to dynamics experiments in which the time for a body to fall through measured distances is determined, and g is calculated from the equation of motion (see Topic 3).

Example

A helical spring is damped at one end and hangs vertically. It extends by IOcm when a rnass of 50g is hung from its free end. Calculate:

(a) the spring constant of the spring,

(b) the period of small amplitude oscillations of the mass.

(a) Using k the spring constant k = 50 x 10-2 x 9.8/10 x 10-2 = 4.9N m-l (b) Using T = the period T = (50 x 10-3/4.9) 0.63s.

Now it's your turn

2   The acceleration of free fall at the Earth's surface is 9.8m s-2. Calculate the length of a simple pendulum which would have a period of 1.0s.

3   The acceleration of free fall on the Moon's surface is 1.6m s-2 . Calculate, for the pendulum in question 2, its period of oscillation on the Moon.

13.2 Energy changes in simple harmonic motion

Kinetic energy

On page 233, we saw that the velocity of a particle vibrating with simple harmonic mction varies with time and, consequently, with the displacement of the particle.

x

Figure 13.10 Variation of kinetic energy in s.h.m.

—xo                                 o                                 xo

Figure 13.11 Variation of potential energy in s.h.m_

For the case where displacement x is zero at time t = O, displacement and velocity are given by x = xo sin

v xoo cos

There is a trigonometrical relation between the sine and the cosine of an angle 0, which is sin² e + cos² 9 = 1. Applying this relation, we have x²/x0² + v²/x0²a'² = 1 which leads to

"2 x020 _ and so v =  (x02 _ x.2)

(If we had taken the displacement and velocity equations for the case when the displacement is a maximum at t = O, exactly the same relation would have been obtained. Try it!)

The kinetic energy of the particle (of mass m) oscillating with simple harmonic motion is                                        Thus, the kinetic energy Ek at displacement x is given by

Ek = -Im0²(x0² — x² )

The variation with displacement of the kinetic energy is shown in Figure 13.10.

Potential energy

The defining equation for simple harmonic motion can be expressed in terms of the restoring force acting on the particle. Since F = ma and a = —ex then at displacement x, this force is

Fro = —moh

where m is the mass of the particle. To find the change in potential energy of the particle when the displacement increases by Ax, we need to find the work done against the restoring force.

The work done in moving the point of application of a force F by a distance Ax is FAX. In the case of the particle undergoing simple harmonic motion, we know that the restoring force is directly proportional to displacement. To calculate the work done against the restoring force in giving the particle a displacement x, we take account of the fact that depends on x by taking the average value of during this displacement. The average value is just hmm; since the value of F is zero at x = 0 and increases linearly to moyx at displacement x. Thus, the potential energy Ep at displacement x is given by averar restoringforce x displacement, or

Ep = \m0²x²

The variation with displacement of the potential energy is shown in Figure 13.11.

Figure 13.12 Energy variations in s.h.m.

Total energy

The total energy Etot of the oscillating particle is given by

Etot Ek + E

^L m0² (x0² — x² ) + ^L m0²x²

This total energy is constant since m, and xo are all constant. We might have expected this result, as it merely expresses the law of conservation of energy.

The variations with displacement x of the total energy Etot, the kinetic energy Ek and the potential energy Ep are shown in Figure 13.12.

A particle of mass 60g oscillates in simple harmonic motion with angular frequency

6.3rad s-1 and amplitude 15 mm. Calculate

(a) the total energy,

(b) the kinetic and potential energies at half-amplitude (at displacement x 7.5 mm). (a) Using Etot = yn0²x0² ,

*6.3² x(15 x lo-3 )²

= 2.7 x 10-4 J

(don't forget to convert g to kg and mm to m)

          (b)           Using Ek =

lo-³ - (7.5 x 10-3 )²J

Using Ep

²

r•-bte that Etot = Ek + Ep, as expected.

Now it's your turn

4 A particle of mass 0.40kg oscillates in simple harmonic motion with frequency 5.0 Hz and amplitude 12cm. Calculate, for the particle at displacement IOcm:

(a) the kinetic energy  the potential energy (c) the total energy.

13.3 Free and damped oscillations

A particle is said to be undergoing free oscillations when the only external force acting on it is the restoring force

There are no forces to dissipate energy and so the oscillations have constant amplitude.

Total energy remains constant. This is the situation we have been considering so far. Simple harmonic oscillations are free oscillations.

In real situations, however, frictional and other resistive forces cause the oscillator's energy to be dissipated, and this energy is converted eventually into thermal energy. The oscillations are said to be damped

The total energy of the oscillator decreases with time. The damping is said to be light when the amplitude of the oscillations decreases gradually with time. This is illustrated in Figure 13.13. The decrease in amplitude is, in fact, exponential with time. The period of the cscillation is slightly greater than that of the corresponding free oscillation.

Heavy damping causes the oscillations to die away more quickly. If the damping is increased further, then the system reaches critical damping point. Here the displacement decreases to zero in the shortest time, without any oscillation (Figure 13.14).

Any further increase in damping produces overdamping. The displacement decreases to zero in a longer time than for critical damping (Figure 13.14).

Figure 13.14 Critical damping and overdamping

Figure 13.15 Vehicle suspension system showing springs and dampers

Damping is useful in an oscillating system. For example, vehicles have springs between the wheels and the frame to give a smcnher and more comfortable ride (Figure 13.15). If there was no damping, a vehicle would move up and down for some time after hitting a bump in the road. Dampers (shock absorbers) are connected in parallel with the springs that the suspension has critical damping and comes to in the shorest time possible. Dampers often work through hydraulic action. When the spring is compressed, a piston connected to the vehicle frame forces oil through a small hole in the piston, so that the energy of the oscillation is dissipated as thermal energy in the oil.

Many swing doors have a damping mechanism fitted to them. The purpose of the damper is so that the open door, when released, does not overshoot the closed position with the possibility of injuring someone approaching the door. Most door dampers operate in the overdamped mode.

Forced oscillations and resonance

When a vibrating body undergoes free (undamped) oscillations, it vibrates at its natural frequency. We met the idea of a natural frequency in Topic 13, when talking about stationary waves on strings. The natural frequency of such a system is the frequency of the first mode of vibration; that is, the fundamental frequency. A practical example is a guitar string, plucked at its centre, which oscillates at a particular frequency that depends on the speed of progressive waves on the string and the length of the string. The speed of progressive waves on the string depends on the mass per unit length of the string and the tension in the string.

Vibrating objects may have periodic forces acting on them. These periodic forces will make the object vibrate at the frequency of the applied force, rather than at the natural frequency of the system. The object is then said to be undergoing forced vibrations. Figure 13.16 illustrates apparatus which may be used to demonstrate the forced vibrations of a mass on a helical spring. The vibrator provides the forcing (driving) frequency and has a constant amplitude of vibration.

As the frequency of the vibrator is gradually increased from zero, the mass begins to oscillate. At first the amplitude of the oscillations is small, but it increases with increasing frequency. When the driving frequency equals the natural frequency of oscillation of the mass—spring system, the amplitude of the oscillations reaches a maximum The frequency at which this occurs is called the resonant frequency, and resonance is said to occur.

Figure 13.20 Time-exposure photographs of Barton's pendulums with light damping taken end-on. The longest arc. in the middle, is the driver.

Figure 13.16 Demonstration of forced oscillations

Resonance occurs when the natural frequency of vibration ofan object is equal to the dri•ing frequency, giving a maximum amplitude of vibration.

If the driving frequency is increased further, the amplitude of oscillation of the mass decreases. The variation with driving frequency of the amplitude of vibration of the mass is illustrated in Figure 13.17. This graph is often called a resonance curve.

resonant driving resonant driving frequency frequency trequency frequency

Figure 13.17 Resonance curve                       Figure 13.18 Effect of damping on the resonance curve

•the amplitude of oscillation at all frequencies is reduced

•the frequency at maximum amplitude shifts gradually towards lower frequencies

•the peak becomes flatter.

BartonS pendulums may be used to resonance and the effects of damping The apparatus consists of a set of light pendulums, made (for example) from paper cones, and a more massive pendulum (the (Inver), all supported on a taut string. The arrangement is illustrated in Figure 13.19. The lighter pendulums have different lengths, tuit one has the sune length as the driver. This has the sime natural frequency as the driver and will, therefore, vibrate with the largest amplitude of all the pendulums (Figure 13.20).

driver

Figure 13.19 Barton's pendulums

Figure 13.21 Pushing a child on a swing makes the swing go higher

Adding weights to the paper cones reduces the effect of damping. With less damping, the amplitude of the resonant pendulum is much larger.

There are many examples of resonance in everyday life. One of the simplest is that of pushing a child on a swing (Figure 13.21). We push at the same frequency as the natural frequency of oscillation of the swing and child, so that the amplitude of the motion increases.

The operation of the engine of a vehicle causes a periodic forte on the parts of the vehicle, which can cause them to resonate. For example, at particular frequencies of rotatim of the engine, the mirrors may resonate. To prevent excessive vibration, the mountings of the mirrors provide damping.

Musical instruments rely on to amplify the sound produced. The sound from a tuning fork is louder when it is held over a tube of just the right length, so that the column of air resonates. We met this phenomenon in 10pic 15, in connection with the resonance tube method of measuring the speed of sound in air. Stringed instruments have a hdlow wooden box with a hole under the strings which acts in a similar way. To amplify all notes from all of the strings, the sounding-box has to be a complex shape so that it resonates at many different frequencies.

A spectacular example of resonance that is often quoted is the failure of the first suspension bridge over the Tacoma Narrows in Washington State, USA. Wind caused the bridge to oscillate. It was used for months even though the road',vay was oscillating with transverse vibrations. Approaching vehicles would appear, and then disappear, as the bridge deck vibrated up and down. One day strong winds set up twisting vibrations (Figure 13.22) and the amplitude of vibration increased due to resonance, until eventually the bridge collapsed. The driver of a car that was on the bridge managed to walk to safety before the collapse, although his dog could not be persuaded to leave the car.

Figure 13.22 The Tacoma Narrows bridge disaster

Examination style questions

A particle is oscillating in simple harmonic motion with period 4.5 ms and amplitude 3.0cm.

At time t = O, the particle is at the equilibrium position. Calculate, for this particle:

a the frequency, b the angular frequency, c the maximum speed, d the magnitude of the maximum acceleration, e the speed attime t= 1.0ms.

2   A particle is oscillating in simple harmonic motion with frequency 50Hz and amplitude 15 mm. Calculate the speed when the displacement from the equilibrium position is 12 mm.

3   Geologists use the fact that the period of oscillation of a simple pendulum depends on the acceleration of free fall to map variations of g A geologist determines the frequency of oscillation of a test pendulum of effective length 515.6 mm to be 0.6948 Hz. Calculate the acceleration of free fall at this locality.

4   A spring stretches by 85 mm when a mass of 50g is hung from it. The spring is then stretched a further distance of 15 mm from the equilibrium position, and the mass is released at time t = O. Calculate: a the spring constant, b the amplitude of the oscillations. c the period, d the displacement at time t = 0.20s. (g = 9.8m s-2)

5   One particle oscillating in simple harmonic motion has ten times the total energy of another particle, but the frequencies and masses are the same. Calculate the ratio of the amplitudes of the two motions.

6   a Calculate the displacement in terms of xo. expressed as a fraction of the amplitude xo of a particle moving in simple harmonic motion with a speed equal to half the maximum value.

b Calculate the displacement at the energy of the particle has equal amounts of kinetic and of potential energy.

7 The apparatus of fig. 13.16 is used to demonstrate forced vibrations and resonance. A 50 g mass is suspended from the spring, which has a spring constant of 7.9N m-l . a Calculate the resonant frequencyfo of the system.

b A student suggests that resonance should also be observed at a frequency of           Discuss this suggestion.

8 a Define simple harmonic motion.

b fig. 13.23a illustrates a U-tubeof uniform crosssectional area A containing liquid of density p. The total length of the liquid column is L. When the liquid is displaced by an amount Ax from its equilibrium position (see Fig. 13.23b), it oscillates with simple harmonic motion.

Ax

A

                           a)                                                           b)

Fig. 13.23

The weight of liquid above AB in Fig. 13.23b provides the restoring force.

i  Write down an expression for the restoring force.

ii Write down an expression for the acceleration of the liquid column caused by this force.

iii             Explain how this fulfils the condition for simple harmonic motion.

Write down an expression for the frequency of the oscillations.

9  A 'baby bouncer' consists of a harness attached to a rubber cord. A baby of mass 6.5kg is placed gently in the harness and the cord extends by 0.40m. The baby is then pulled down another 0.10m and, when released, begins to move with simple harmonic motion. Calculate a the period of the motion, b the maximum force on the baby.

(acceleration of free fall g = 9.8m s-2)

10                    A simple model of a hydrogen molecule assumes that it consists of two oscillating hydrogen atoms connected by a spring of spring constant 1.1 x IO^A N m-l .

a The mass of a hydrogen atom is 1.7 x 10 -27 kg. Calculate the frequency of oscillation of the hydrogen molecule.

b Explain why light of wavelength 2.3 gm would be strongly absorbed by this model of the hydrogen molecule. (speed of light c = 3.0 x 10⁸ m s-1)

11 A ball is held between two fixed points A and B by means of two stretched springs, as shown in Fig. 13.24.

ball

Fig. 13.24

The ball is free to oscillate along the straight line AB. The springs remain stretched and the motion of the ball is simple harmonic.

The variation with time t of the displacement x of the ball from its equilibrium position is shown in Fig. 13.25.

Examination Style questions

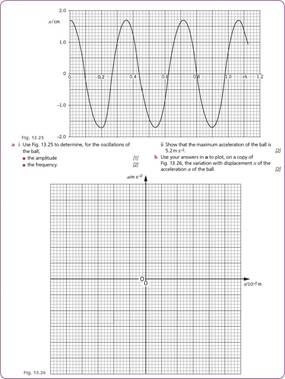
c Calculate the displacement of the ball at which its kinetic energy is equal to one half of the rnaximum kinetic energy.                       [31 Cambridge Intemational AS and A Level Physics, 9702/43 May/June 2013 Q 3

12 A long strip of springy steel is clamped at one end so that the strip is vertical. A mass of 65 g is attached to the free end of the strip, as shown in Fig. 13.27.

springy  65 g steel

Fig. 13.27

The mass is pulled to one side and then released. The variation with time t of the horizontal displacement of the mass is shown in Fig. 13.28.

The mass undergoes damped simple harmonic motion.

Explain what is meant by damping. [2] ii Suggest, with a reason, whether the damping is light, critical or heavy.                          [2]

Use Fig.13.28 to determine the frequency of vibration of the mass.

ii Hence shon that the iritid energy stcred in the steel strip before the mas is released is approximates' 3.2mJ. [2]

c After eight complete oscillations of the mass, the amplitude of vibration is reduced from 1.5cm to 1 .1 cm. State and explain whether, after a further eight complete oscillations, the amplitude will be 0.7 cm. [21 Cambridge International AS and A Level Phyöcs,

9702/42 May/June 2010 Q 2

13 A small metal ball is suspended from a fixed point by means of a string, as shown in Fig. 13.29.

string

ball

Fig. 13.29

The ball is pulled a small distance to one side and then released. The variation with time t of the horizontal displacementx of the ball is shown in Fig. 13.30. The motion of the ball is simple harmonic.

a Use data from Fig. 13.30 to determine the horizontal acceleration of the ball for a displacement x of 2.0 cm.

[3]

2

displacement lcm

o

mg. 13.28

Examination style questions

The variation with frequency of the amplitude of the oscillations of the metal cube is shown in Fig. 13.33.

a i State the phenornenon illustrated in Fig. 13.33. [1] ii For the maximum amplitude of vibration, state the magnitudes of the amplitude and the frequency. [1] b The oscillations of the metal cube of mass 150g may be assumed to be simple harmonic.

Use your answers in a ii to determine, for the metal cube, i its maximum acceleration, [31 ii the maximum resultant force on the cube. [2]

15

amplitude

                                                        Imm        10

5

                                         2              4

Fig. 13.33

c Sorne very light feathers are attached to the top surface of the cube so that the feathers extend outwards, beyond the vertical sides of the cube.

The investigation is now repeated.

On a copy of Fig. 13.33, draw a line to show the new variation with frequency of the amplitude of vibration for frequencies between 2 Hz and 10 Hz.    [21 Cambridge Intemational AS and A Level Physics, 9702/42 Oct/Nov 2010 Q 3

6                                      10 frequency/Hz