Поделиться
Практическое занятие 1.doc
Системы классификации и кодирования информации.
Представление чисел в различных системах счисления. Перевод чисел из одной системы в другую.
Совокупность приемов наименования и записи чисел называется счислением. Под системой счисления понимается способ представления любого числа с помощью ограниченного алфавита (набора) символов, называемых цифрами.
Одно и то же число может быть представлено в различных системах счисления. Привычной для нас является десятичная система счисления, в которой для записи чисел используются 10 различных цифр: 0, 1, 2, ..., 9.
Счисление представляет собой частный случай кодирования, где слово, записанное с использованием определенного алфавита и по определенным правилам, называется кодом. Применительно к счислению это код числа.
Различают позиционные и непозиционные системы счисления.
В непозиционных системах счисления каждое число обозначается соответствующей совокупностью символов.
Пример – римская система счисления со сложным способом записи чисел и громоздкими правилами выполнения арифметических операций. Например, запись MCMXCVIII означает число 1998 (М – тысяча, С – сто, Х – десять, V – пять, I – единица и т.д.)
В позиционных системах счисления значение числа определяется не только набором входящих в него цифр, но и их местом (позицией) в последовательности цифр, изображающих это число.
Пример – десятичная система счисления. Например, числа 127 и 721.
Количество символов, используемых в позиционной системе счисления, называется ее основанием. В десятичной системе счисления используется десять символов (цифр): 0. 1, 2, 3, 4, 5, 6, 7, 8, 9, и основанием системы является число десять.
Особое место среди позиционных систем счисления занимают системы со степенными весами разрядов, в которых веса смежных позиций цифр (разрядов) отличаются по величине в постоянное количество раз, равное основанию системы счисления.
В общем случае в такой позиционной системе счисления с основанием q любое число Х может быть представлено в виде полинома разложения:
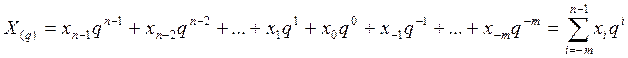, (1.1)
где X(q) – запись числа в системе счисления с основанием q;
q - основание системы счисления;
хi - целые числа, меньше q;
n - число разрядов (позиций) в целой части числа;
m - число разрядов в дробной части числа.
Пример: 4295,67 (10) = 4 · 103 + 2 · 102 + 9 · 101 + 5 · 100 + 6 · 10-1 + 7 · 10-2
Изображение числа X(q) в виде последовательности коэффициентов хi полинома является его условной сокращенной записью (кодом).
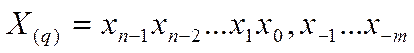(1.2)
Запятая отделяет целую часть от дробной и служит началом отсчета значений веса каждой позиции (разряда).
В информатике применяют позиционные системы счисления с недесятичным основанием: двоичную, восьмеричную и шестнадцатеричную. т. е. системы счисления с основанием q = 2k, где k = 1, 3, 4.
В литературе часто встречаются сокращенные обозначения систем счисления:
Dec - десятичная система (decimal);
Bin - двоичная система (binary);
Hex - шестнадцатеричная система (hexadecimal).
В двоичной системе счисления для представления любого числа используются два символа – цифры 0 и 1. Основание системы счисления
q = 2.
Произвольное число с помощью формулы (1.1) можно представить в виде разложения по степеням двойки:
,
Тогда условная сокращенная запись в соответствии с (1.2) означает изображение числа в двоичной системе счисления (двоичный код числа), где хi = 0 или 1. Например:
13,625 (10) = 1 · 23 + 1 · 22 + 0 · 21 + 1 · 20 + 1 · 2-1 + 0 · 2-2 + 1· 2-3 = 1101,101(2)
Двоичное представление числа требует примерно в 3,3 раза большего числа разрядов, чем его десятичное представление. Тем не менее применение двоичной системы счисления создает большие удобства для работы ЭВМ, т. к. для представления в машине разряда двоичного числа может быть использован любой запоминающий элемент, имеющий два устойчивых состояния.
Арифметические действия над одноразрядными двоичными числами выполняются по следующим правилам:
0+0=0 0х0=0.
0+1=1 0х1=0
1+0=1 1х0=0
1+1=10 1х1=1.
В восьмеричной системе счисления алфавит состоит из восьми символов (цифр): 0, 1 ... 7. Основание системы счисления q = 8. Для записи произвольного числа в восьмеричной системе счисления необходимо по формуле (1.1) найти его разложение по степеням восьмерки, а затем воспользоваться условной сокращенной записью (1.2).
Например, десятичное число 28(10) = 3 · 81 + 4· 80 = 34(8)
Восьмеричное изображение (код) основания системы счисления
q = 8(10) = 10 (8)
В шестнадцатеричной системе счисления алфавит включает в себя 16 символов (цифр и букв): 0, 1 ... 9, А, В, С, D, Е, F. Основание системы счисления q = 16. Для записи произвольного числа в этой системе счисления необходимо по формуле (1.1) найти его разложение по степеням 16, а по формуле (1.2) — код.
Например: 75(10) = 44 · 161 + В· 160 = 4В (16).
Шестнадцатеричное изображение основания системы счисления q = 16(10) =10 (16).
Для сравнения в табл. 1.1 приведены коды одних и тех же чисел в разных системах счисления.
|
|
|
|
|
|
|
|
|
|
||||
|
Коды чисел в различных системах cчисления |
Таблица 1.1 |
|||||||||||
|
|
Х(10) |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
|
|
|
Х(2) |
0 |
1 |
10 |
11 |
100 |
101 |
110 |
111 |
1000 |
|
|
|
|
Х(8) |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
10 |
|
|
|
|
Х(16) |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 ' |
8 |
|
|
|
|
Х(10) |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
|
|
|
|
Х(2) |
1001 |
1010 |
1011 |
1100 |
1101 |
1110 |
1111 |
10000 |
10001 |
|
|
|
|
Х(8) |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
20 |
21 |
|
|
|
|
Х(16) |
9 |
А |
В |
С |
D |
Е |
F |
10 |
11 |
|
|
Наряду с двоичными кодами, которыми оперирует ЭВМ, для ввода и вывода десятичных чисел (данных) используют специальное двоично-десятичное кодирование. При двоично-десятичном кодировании каждая десятичная цифра заменяется тетрадой (четверкой) двоичных цифр, а сами тетрады записываются последовательно в соответствии с по рядком следования десятичных цифр. При обратном преобразовании двоично-десятичного кода в десятичный исходный код разбивается на тетрады вправо и влево от запятой, которые затем заменяются десятичными цифрами.
Таким образом, при двоично-десятичном кодировании фактически не производится перевод числа в новую систему счисления, а мы имеем дело с двоично-кодированной десятичной системой счисления.
Например, десятичное число 15(10) = F(16) = 17(8) = 1111(2) = 00010101(2-10).
ЭВМ работают с двоичными кодами, пользователю удобнее иметь дело с десятичными или шестнадцатеричными. Поэтому возникает необходимость перевода числа из одной системы счисления в другую.
Преобразование числа X из системы счисления с основанием q в систему счисления с основанием р (преобразование Х(q) → Х(р)) осуществляется по правилу замещения или по правилу деления-умножения на основание системы счисления.
Правило замещения реализуется на основании формулы (1.1) и предусматривает выполнение арифметических операций с кодами чисел в новой системе счисления. Поэтому оно чаще всего используется для преобразования чисел из недесятичной системы счисления в десятичную.
Пример. Выполнить преобразование Х(2) → Х(10), если Х{2) =10101,011
Х(10) = 1 · 24 + 0 · 23 + 1 · 22 + 0 · 21 + 1 · 20 + 0 · 2-1 + 1 · 2-2 + 1 · 2-3 = 21,375
Правило деления-умножения предусматривает выполнение арифметических операций с кодами чисел в исходной системе счисления с основанием q, поэтому его удобно применять для преобразования десятичных чисел в любые другие позиционные системы счисления. Правила преобразования целых чисел и правильных дробей различны. Для преобразования целых чисел используется правило деления, а для преобразования правильных дробей — правило умножения. Для преобразования смешанных чисел используются оба правила соответственно для целой и дробной частей числа.
Правило деления
используется для преобразования целого числа, записанного в q - ичной системе
счисления, в р -ичную. В этом случае необходимо последовательно делить
исходное q -ичное число и получаемые частные
на новое основание р, представленное в q -ичной
системе счисления. Деление продолжают до тех пор, пока очередное частное не
станет меньше р. После замены полученных остатков и последнего частного
цифрами р -ичной системы счисления записывается код числа в новой
системе счисления. При этом старшей цифрой является последнее частное, а
следующие за ней цифры соответствуют остаткам, записанным в последовательности,
обратной их получению.
Правило умножения используется для преобразования дробного числа, записанного в q -ичной системе счисления, в р -ичную. В этом случае необходимо последовательно умножать исходную дробь и дробные части получающихся произведений на основание р, представленное в исходной q -ичной системе счисления. Целые числа получаемых произведений, замененные цифрами р-ичной системы счисления, и дают последовательность цифр в новой р -ичной системе.
Умножение необходимо производить до получения в искомом р -ичном коде цифры того разряда, вес которого меньше веса младшего разряда исходной q -ичной дроби. При этом в общем случае получается код приближенно, и всегда с недостатком значения дроби. Поэтому в случае обратного преобразования (р -ичного кода дроби в q -ичный) результат может не совпадать с исходным значением q -ичной дроби.
Пример. Выполнить преобразование
Х(10) → Х(2), если Х{10) =37,45
Для получения частных и остатков по правилу деления для целой части числа удобно использовать формулу записи, известную под названием «деление в столбик», а для получения р -ичного кода дробной части числа по правилу умножения — форму записи, известную под названием «умножение столбиком». Применительно к рассматриваемому примеру имеем:
|
37 |
2 |
|
|
|
|
|
|
36 |
18 |
2 |
|
|
|
|
|
1 |
18 |
9 |
2 |
|
|
|
|
← |
0 |
8 |
4 |
2 |
|
|
|
|
← |
1 |
4 |
2 |
2 |
|
|
|
|
← |
0 |
2 |
1 |
- последнее частное |
|
|
|
|
← |
0 |
↓ |
|
|
|
|
|
|
← |
← |
|
целая часть Х(2) = 100101
|
↓ |
0, |
45 х 2 |
|
↓ |
0 |
90 х 2 |
|
↓ |
1 |
80 х 2 |
|
↓ |
1 |
60 х 2 |
|
↓ |
1 |
20 |
|
↓ |
. . . |
… |
дробная часть Х(2) = 0,0111
Таким образом, в результате преобразования получаем 37,45(10) = 100101,0111... (2)
Как
следует из примера, процесс перевода дробной части можно продолжить до бес-конечности.
ЭВМ оперирует числами, представленными конечными наборами цифр. 
Поэтому дроби
округляют в соответствии с правилами преобразования и весом младшего разряда
исходной дроби.
Преобразование чисел из двоичной системы счисления в восьмеричную, шестнадцатеричную и обратно осуществляется по упрощенным правилам с учетом того, что основания этих систем счисления кратны целой степени 2, т. е. 8= 23, а 16 = 24 . Это означает, что при преобразовании восьмеричного кода числа в двоичный, необходимо каждую восьмеричную цифру заменить соответствующим трехзначным двоичным кодом (триадой).
При преобразовании шестнадцатеричного кода числа в двоичный необходимо каждую шестнадцатеричную цифру заменить четырехзначным двоичным кодом (тетрадой).
При преобразовании двоичного кода в восьмеричный или шестнадцатеричный двоичный код делится соответственно на триады или тетрады влево и вправо от запятой (точки), разделяющей целую и дробные части числа. Затем триады (тетрады) заменяются восьмеричными (шестнадцатеричными) цифрами:
Например: 1CD,4(16) = 000111001101,0100(2) = 0715,2(8).
Если при разбиении двоичного кода в крайних триадах (тетрадах) недостает цифр до нужного количества, они дополняются нулями. Соответственно, «лишние» нули слева и справа, не вошедшие в триады (тетрады) отбрасываются.
ТЕКСТ - это последовательность символов.
СИМВОЛ - это отдельная буква (латинского или национального алфавита), цифра (0, 1, ..., 9), знак препинания (.,:;?! и так далее), дополнительный символ (@#$%^& и так далее), некоторые другие символы.
Одним из распространенных видов информации, обрабатываемой на компьютерах, является текстовая информация или текст.
Любая информация перед ее обработкой на компьютере должна быть представлена в числовой форме - а именно, в двоичной числовой форме;. текстовая информация не является исключением.
При преобразовании текстов в числовую форму каждый символ представляется (кодируется) в виде двоичной последовательности определенной длины.
Ввод текстовой информации осуществляется с помощью специальных внешних устройств (например, клавиатура). Сигналы, поступающие от символьных клавиш автоматически (с помощью аппаратных средств или специальных программ) представляются в виде двоичных чисел.
Обычно количество символов, с которыми оперирует компьютер, равно 256.
Для того чтобы представить все 256 символов с помощью разных двоичных последовательностей, длина этих последовательностей должна быть равна 8 битам или 1 байту.
Например:
Символ Двоичное представление
0 00110000
1 00110001
S 01010011
* 00101010
и т.д.
Кодировка символов осуществляется с помощью специальных таблиц, в которых все 256 символов расположены в определенном порядке и имеют десятичные номера от 0 до 255. Для перевода символа в двоичное представление достаточно перевести его десятичный номер в двоичную форму.
Например:
Буква S в таблице кодировки имеет порядковый номер 83. Двоичный эквивалент этого десятичного числа равен 01010011.
Различных таблиц кодировок символов достаточно много. Они отличаются друг от друга конкретным набором символов и порядком их расположения в таблице. Наиболее распространенными (в России) являются таблица с АЛЬТЕРНАТИВНОЙ кодировкой или с МОДИФИЦИРОВАННОЙ АЛЬТЕРНАТИВНОЙ кодировкой.
Во многих микропроцессорных системах и персональных ЭВМ для представления алфавитно-цифровых символов используется код ASCII (American Standart Code for Information Interchange — американский код обмена информацией), расширенный путем добавления букв русского алфавита. Для представления каждого символа также отводится один байт. Следует подчеркнуть, что все виды представления символьной информации отличаются только кодировкой символов.
Задания для самостоятельной работы
Задание 1
1. Выбрать число Х(10), (целая часть – 3 разряда, дробная часть – 3 разряда)
2. Выполнить преобразование Х(10) → Х(2)
3. Выполнить обратное преобразование Х(2) → Х(10)
4. Выполнить преобразование Х(10) → Х(8)
5. Выполнить обратное преобразование Х(8) → Х(10)
6. Выполнить преобразование Х(10) → Х(16)
7. Выполнить обратное преобразование Х(16) → Х(10)
8. Выполнить преобразование Х(10) → Х(5)
9. Выполнить преобразование Х(5) → Х(6)
10. Выполнить преобразование Х(16) → Х(20)
Задание 2
Вычислить
1. 111(2) + 111(2) = Х(10)
2. 777(8) + 777(8) = Х(10)
3. 1CD,4(16) + 1CD,4(16) = Х(10)
Задание 3.
Выбрать Х – число страниц в тексте, Y – число символов на странице.
В текстовом файле хранится текст объемом в Х страниц. Каждая страница содержит Y символов. Если используется кодировка KOI-8 (8 бит на один символ), то размер файла в байтах составит - ?
Скачано с www.znanio.ru
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.
