_Составление математической модели для решения прикладных задач

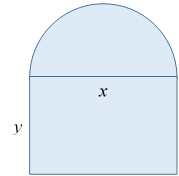
1) Нормандское окно имеет форму прямоугольника, завершенного полукругом. В архитектуре часто используется такая форма окна. Дан периметр нормандского окна P. Каковы должны быть его размеры, чтобы оно пропускало наибольшее количество света?

Решение.

Пусть x – основание, а y – высота прямоугольника, тогда . Выразим высоту прямоугольника:

. Следовательно, площадь окна выражается формулой

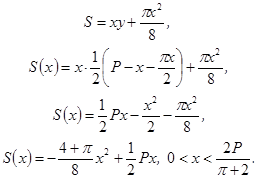
Площадь представляет собой квадратичную функцию, старший коэффициент которой отрицателен. Следовательно, свое наибольшее значение она будет принимать при  или .

Т.к.  и то

Итак, наибольшую площадь при заданном периметре нормандское окно будет иметь при  и .

Ответ: Размеры прямоугольной части окна должны быть равны

2) Имеется проволока длиной l. Требуется согнуть ее так, чтобы получился прямоугольник, ограничивающий наибольшую площадь.

Решение.

Пусть стороны прямоугольника рывны х и у, тогда . Отсюда  .

Найдем площадь прямоугольника:

Поскольку старший коэффициент полученной квадратичной функции отрицателен, то свое наибольшее значение она принимает в вершине параболы:

 ,

 ,

.

Ответ: чтобы получился прямоугольник, ограничивающий наибольшую площадь, нужно проволоку согнуть в форме квадрата.