Свойства арифметического квадратного корня_Методические рекомендации к уроку №3

Методические рекомендации к проведению урока

Тема урока: Свойства арифметического квадратного корня

Тип урока: Изучение новой темы

Цели обучения:

8.1.2.1

применять свойства арифметического квадратного корня;

Цели урока:

Учащиеся могут применять свойства арифметического квадратного корня для вычисления значений квадратных корней и преобразования выражений, содержащих квадратные корни.

Структура урока

1.    Организационный момент.

2.    Стадия вызова.

3.    Целеполагание.

4.    Объяснение нового материала и его первичное закрепление.

5.   Закрепление изученного материала.

·         Работа в парах

·         Индивидуальная работа

6.   Подведение итогов урока.

Теоретический материал к уроку, определения к понятиям и др.

Теорема 1. Если  и , то .

Корень из произведения неотрицательных множителей равен произведению корней этих множителей.

Следствие. 1-теорема распространяется на случай, когда число множителей под знаком корня больше двух.

Доказательство. 1) Если а ³ 0, b ³ 0 , то , , следовательно, .

2)

Следовательно, по определению арифметического квадратного корня, , ч.т.д.

Обобщение: Если а_k ³ 0, то .

Теорема 2. Если  и , то .

Корень из дроби, числитель которого неотрицателен, а знаменатель положителен, равен корню из числителя, деленному на корень из знаменателя.

Доказательство. 1) Если а ³ 0, b > 0 , , следовательно, .

2) .

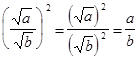Следовательно, по определению арифметического квадратного корня, , ч.т.д.

Теорема 3. При любом значении х верно равенство .

Доказательство. 1) если xÎR, то x² ³ 0, то есть, выражение в левой части имеет смысл и |x| ³ 0;

2) |x|² = (±x)² = x².

Следовательно, по определению арифметического квадратного корня, , ч. т. д.

Следствие. Если xÎR, nÎN .     x²ⁿ = (xⁿ)²

Чтобы извлечь корень из степени с четным показателем, надо представить подкоренное выражение в виде квадрата некоторого выражения и использовать рассмотренное тождество.

Инструкции к демонстрациям и технике безопасности.

Демонстрация материала осуществляется с помощью презентации PowerPoint. Слайды презентации содержат анимации, которые позволяют поэтапно вывести на экран решения и ответы к предложенным заданиям или продемонстрировать ответы на заданные вопросы. Поэтому при показе презентации следует делать паузы после демонстрации заданий и постановки вопросов, давая время учащимся на их выполнение и обдумывание ответов.

Дополнительные методические рекомендации по организации урока.

Структура и организация урока нацелены на продуктивную деятельность учащихся при изучении новой темы, не допуская пассивного восприятия материала. В связи с этим учителю необходимо задавать учащимся вопросы высокого порядка, наталкивая их на «открытие» и освоение нового материала, при этом выдерживая паузы, необходимые для обдумывания.    

Дополнительные разноуровневые (на дифференциацию) задания.

Желтая – базовый уровень.  Зелёная – конструктивный уровень.

Рекомендации по формативному оцениванию.

Формативное оценивание производится на каждом этапе урока (самооценивание, оценивание учителем по критериям, а также посредством наблюдения). Оценка путем наблюдения за вовлечением учеников в работу при выполнении заданий и за участием в диалогах. Прогресс, ответную реакцию на задания в парах необходимо отслеживать для того, чтобы оценить вклад каждого ученика и выявить наличие ошибок для их дальнейшей коррекции.

Ответы, критерии к заданиям, дополнительные материалы к уроку.

Ответы к заданиям, выполненным в процессе первичного закрепления изученного, содержатся в презентации урока и полезны для организации самооценивания учащихся.

Критерии оценивания к каждому заданию прописаны в приложениях к уроку, а также указаны в краткосрочном плане.

Ответы к приложению 1.

1.       4,8; 4; 24; 6; 45; 5/6; 1/10; 40/9.

2.       «Собери цепочку».

Ответ к приложению 2. Ключевое слово: ЕРМЕКОВ.

Алимхан Абеуович Ермеков (1891 -1970) — казахский общественный деятель, первый казахский профессор-математик. Окончил Томский технологический институт (1921 г.).

В 1930-х годах активно занимался разработкой учебных пособий по математике на казахском языке. Алимхан Ермеков издал в 1935 г. на казахском языке (на латинской графике) учебник для вузов по высшей математике, а также словарь математических терминов «Қазақ тіліндегi математика терминдері».

Основные направления научно-исследовательской трудов — математическая статистика, теоретическая механика, вопросы математической терминологии.

Список полезных ссылок и литературы.

Предлагаются ссылки на интернет-уроки по теме «Определение арифметического квадратного корня и его свойства». В каждой ссылке можно найти конспект к уроку.

1.      Свойства квадратных корней.

http://interneturok.ru/ru/school/algebra/8-klass/funktsiya-y-x-svoystva-kvadratnogo-kornya/svoystva-kvadratnyh-korney?seconds=0&chapter_id=920

2.      Свойства квадратных корней. Решение задач.

http://interneturok.ru/ru/school/algebra/8-klass/funktsiya-y-x-svoystva-kvadratnogo-kornya/svoystva-kvadratnyh-korney-reshenie-zadach?seconds=0&chapter_id=920

Скачано с www.znanio.ru