Свойства арифметического квадратного корня_Методические рекомендации к уроку №5 (1)

Методические рекомендации к проведению урока

Тема урока: Свойства арифметического квадратного корня

Тип урока: Урок закрепления знаний

Цели обучения:

8.1.2.1

применять свойства арифметического квадратного корня;

Цели урока:

Учащиеся могут применять свойства арифметического квадратного корня для вычисления значений квадратных корней и преобразования выражений.

Структура урока

1.    Организационный момент. Целеполагание.

2.    Проверка домашнего задания.

3.    Математический софизм.

4.    Закрепление знаний.

5.   Подведение итогов урока. Рефлексия.

Теоретический материал к уроку, определения к понятиям и др.

Теорема 3. При любом значении х верно равенство .

Следствие. Если xÎR, nÎN .    

Чтобы извлечь корень из степени с четным показателем, надо представить подкоренное выражение в виде квадрата некоторого выражения и использовать тождество из теоремы 3.

Математический софизм.

К обеим частям равенства  прибавим число  ,

  или

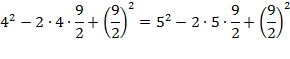
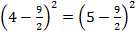 , откуда

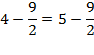
4=5, то есть .

Учитель предлагает учащимся указать ошибку при доказательстве. Учащиеся должны сказать, что в четвертой строке было не верно выполнено возведение в квадрат обеих частей равенства, то есть .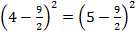

Учитель показывает, что  .

По свойству корней  , и при извлечении квадратного корня из обеих частей равенства должно быть  . Если открыть модуль, то  . Теперь равенство верно.

Модуль числа:

Инструкции к демонстрациям и технике безопасности.

Демонстрация материала осуществляется с помощью презентации PowerPoint. Перед показом слайдов учителю следует ознакомиться с презентацией. Необходимый материал для урока был взят из учебников и с сайта www.bilimland.kz. Если имеется подписка на этот сайт, то можно использовать его ресурсы при подготовке уроков.

Задания, оформленные отдельным приложением, несмотря на то, что они включены в презентацию, необходимо предоставить учащимся обязательно в распечатанном виде.  А имеющиеся слайды использовать при обсуждении с классом и при оценивании выполненной работы. Это поможет свести к минимуму использование интерактивной доски.

Дополнительные методические рекомендации по организации урока.

Структура и организация урока нацелены на продуктивную деятельность учащихся при закреплении изученного, не допуская пассивного восприятия материала. В связи с этим учителю необходимо задавать учащимся вопросы высокого порядка, наталкивая их на «открытие» и освоение нового материала, при этом выдерживая паузы, необходимые для обдумывания.    

Для развития творческого мышления учащихся на уроке используется прием «рассказ из 6 слов», когда учащимся необходимо кратко и ёмко выразить вывод о рассмотренном математическом софизме.

В течение урока следует не допускать типичных ошибок у учащихся по данной теме.

Возможные типичные ошибки учащихся: учащиеся часто забывают о том, что результат извлечения квадратного корня есть положительное число, то есть часто учащиеся утверждают, что .

Дополнительные разноуровневые (на дифференциацию) задания.

Рекомендации по формативному оцениванию.

Формативное оценивание производится на каждом этапе урока (самооценивание, оценивание учителем по критериям, а также посредством наблюдения). Оценка путем наблюдения за вовлечением учеников в работу при выполнении заданий и за участием в диалогах. Прогресс, ответную реакцию на задания в парах необходимо отслеживать для того, чтобы оценить вклад каждого ученика и выявить наличие ошибок для их дальнейшей коррекции.

Ответы, критерии к заданиям, дополнительные материалы к уроку.

Критерии оценивания к каждому заданию указаны в краткосрочном плане.

Ответы к приложению 1.

№1: а) ; b) ; c) -1.

№2: a) a-3; б) 4-b; в) 2; г) 8-2а.

№3: a) 1-m; б) 1-3m; в) 2у-12; г) 6.

№4: б) ; в) ; г) .

№5: а) 4; б) 6; в) 2; г) 10.

Список полезных ссылок и литературы.

Алгебра. 8-класс: Учебник для 8 класса общеобразовательной школы с русским языком обучения/ А.Н. Шыныбеков – 3-издание. – Алматы: «Атамұра», 2012. 288 с.

Галицкий М.Л., Гольдман А.М., Звавич Л.И. Сборник задач по алгебре для 8-9 кл. Москва «Просвещение» 2001.

Білімлэнд, www.bilimland.kz

Скачано с www.znanio.ru