Свойства арифметического квадратного корня_Методические рекомендации к уроку №5

Методические рекомендации к проведению урока

Тема урока: Свойства арифметического квадратного корня

Тип урока: Урок закрепления знаний

Цели обучения:

8.1.2.1

применять свойства арифметического квадратного корня;

Цели урока:

Учащиеся могут применять свойства арифметического квадратного корня для вычисления значений квадратных корней, преобразования выражений и доказательства равенств, содержащих квадратные корни.

Структура урока

1.    Организационный момент. Целеполагание.

2.    Задание «10 секунд на размышление».

3.    Задача Эйлера.

4.    Тест.

5.    Полезно знать, что…

6.    Решение дифференцированных заданий.

7.   Подведение итогов урока.

Теоретический материал к уроку, определения к понятиям и др.

Теорема 1. Если  и , то .

Корень из произведения неотрицательных множителей равен произведению корней этих множителей.

Следствие. 1-теорема распространяется на случай, когда число множителей под знаком корня больше двух.

Доказательство. 1) Если а ³ 0, b ³ 0 , то , , следовательно, .

2)

Следовательно, по определению арифметического квадратного корня, , ч.т.д.

Обобщение: Если а_k ³ 0, то .

Теорема 2. Если  и , то .

Корень из дроби, числитель которого неотрицателен, а знаменатель положителен, равен корню из числителя, деленному на корень из знаменателя.

Доказательство. 1) Если а ³ 0, b > 0 , , следовательно, .

2) .

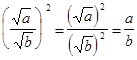Следовательно, по определению арифметического квадратного корня, , ч.т.д.

Теорема 3. При любом значении х верно равенство .

Доказательство. 1) если xÎR, то x² ³ 0, то есть, выражение в левой части имеет смысл и |x| ³ 0;

2) |x|² = (±x)² = x².

Следовательно, по определению арифметического квадратного корня, , ч. т. д.

Следствие. Если xÎR, nÎN .     x²ⁿ = (xⁿ)²

Чтобы извлечь корень из степени с четным показателем, надо представить подкоренное выражение в виде квадрата некоторого выражения и использовать рассмотренное тождество.

Утверждение. Для любого неотрицательного действительного числа a и натурального n справедливо равенство

Утверждение. Пусть а, b, m и n – действительные числа такие, что a=m+n, b=mn. Тогда справедливы равенства:

Инструкции к демонстрациям и технике безопасности.

Демонстрация материала осуществляется с помощью презентации PowerPoint. Слайды презентации содержат анимации, которые позволяют поэтапно вывести на экран решения и ответы к предложенным заданиям или продемонстрировать ответы на заданные вопросы. Поэтому при показе презентации следует делать паузы после демонстрации заданий и постановки вопросов, давая время учащимся на их выполнение и обдумывание ответов.

Дополнительные методические рекомендации по организации урока.

Структура и организация урока нацелены на продуктивную деятельность учащихся при закреплении изученного, не допуская пассивного восприятия материала. В связи с этим учителю необходимо задавать учащимся вопросы высокого порядка, наталкивая их на «открытие» и освоение нового материала, при этом выдерживая паузы, необходимые для обдумывания.    

Дополнительные разноуровневые (на дифференциацию) задания.

Рекомендации по формативному оцениванию.

Формативное оценивание производится на каждом этапе урока (самооценивание, оценивание учителем по критериям, а также посредством наблюдения). Оценка путем наблюдения за вовлечением учеников в работу при выполнении заданий и за участием в диалогах. Прогресс, ответную реакцию на задания в парах необходимо отслеживать для того, чтобы оценить вклад каждого ученика и выявить наличие ошибок для их дальнейшей коррекции.

Ответы, критерии к заданиям, дополнительные материалы к уроку.

Критерии оценивания к каждому заданию прописаны в приложениях к уроку, а также указаны в краткосрочном плане.

Ответы к приложениям 1, 2 содержатся в презентации.

Ответы к приложению 3.

а) 6;  б) 7;  в) 9;  г) 7;  д) 5;  е) 11; 

ж) 6;  з)24;  и) 26;  к) 18;  л) 234;  м) 912. 

Ответы к приложению 4.

Уровень А

1.      а)6,3;         б)19,9.

2.      а)-1;          б)-1;                в)1;                 г) .

3.      а) 3;           б) 6.

4.      а) ;               б);             в);                     г).

5.      а);              б);        в);                  г) .

Уровень В

1.      а) 12;    б)-24.

2.      а);                     б);        в);            

г) .

4.      а) 8 и 2;           б) 42 и 2.

5.      а) ;            б) ;           в) .

Уровень С

1.      а);                  б);           в) ;          г) .

2.     

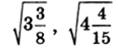
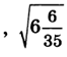
4.      а) 1/6;   б) 102,4.

5.      а) 0; 4;         б) 0; ¼;           в) 2;3;             г) -1; -3/4.

Список полезных ссылок и литературы.

Предлагаются ссылки на интернет-уроки по теме «Определение арифметического квадратного корня и его свойства». В каждой ссылке можно найти конспект к уроку.

1.      Свойства квадратных корней.

http://interneturok.ru/ru/school/algebra/8-klass/funktsiya-y-x-svoystva-kvadratnogo-kornya/svoystva-kvadratnyh-korney?seconds=0&chapter_id=920

2.      Свойства квадратных корней. Решение задач.

http://interneturok.ru/ru/school/algebra/8-klass/funktsiya-y-x-svoystva-kvadratnogo-kornya/svoystva-kvadratnyh-korney-reshenie-zadach?seconds=0&chapter_id=920

Скачано с www.znanio.ru