Свойства арифметического квадратного корня_Разработка урока №5 (1)

Методические рекомендации к уроку №1 темы/подраздела

«Преобразования выражений, содержащих квадратные корни»

раздела 8.1А: Квадратные корни и иррациональные выражения

Тема урока: Вынесение множителя из-под знака корня и внесение множителя под знак корня

Цель обучения:

8.1.2.3

выносить множитель из-под знака корня и вносить множитель под знак корня

На изучение темы Преобразования выражений, содержащих квадратные корни выделено 7 часов. На первом уроке будут рассмотрены такие преобразования, как вынесение множителя из-под знака корня и внесение множителя под знак корня.

Теоретический материал

1. Вынесение множителя за знак корня.

Пусть требуется упростить выражение .

Для этого представим число 75 в виде произведения, в котором один из множителей является квадратом натурального числа, и применим теорему о корне из произведения. Получим:

Мы представили  в виде произведения чисел 5 и . В таких случаях говорят, что мы вынесли множитель за знак корня.

Теперь можно упростить данное выражение:

2. Внесение множителя под знак корня.

Сравним значения выражений

 и .

Представим в выражении  множитель 2 в виде арифметического квадратного корня и выполним умножение корней:

Мы заменили произведение  выражением  . В таких случаях говорят, что мы внесли множитель под знак корня.

Теперь можно сравнить данные выражения. Так как

 < , то  < .

Заметим, что под знак корня можно вносить только неотрицательный множитель. Например, выражение  можно преобразовать, внося под знак корня множитель 5:

Выражение  , где а < 0, можно преобразовать, внося под корень положительный множитель – а:

Источник: Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И., Феоктистов И.Е. Алгебра. 8 класс : учеб. для учащихся общеобразоват. учреждений  – М. : Мнемозина, 2010. – 384 с. : ил.) Пункт 25, страница 154.

Методические рекомендации по организации урока и рекомендации по формативному оцениванию

В начале урока учащиеся выполнят несколько заданий на повторение свойств корней. Затем учитель в процессе беседы обсуждает с учащимися алгоритм выполнения операций внесения множителя из-под знака корня и внесения множителя под знак корня. На слайдах будут поэтапно появляться решения примеров. Следует помогать учащимся правильно использовать математический язык, так как на этом уроке появляются новые термины. На данном уроке будет рассмотрены примеры выполнения указанных преобразований только с числовыми множителями. Примеры, содержащие буквенные множители, рассматриваются на следующем уроке.

Учащиеся будут выполнять достаточно большое количество заданий для отработки навыка в процессе разнообразных видов деятельности. При первичном закреплении во время парной работы предлагается проговаривание учащимися выполняемых действий, это поможет развивать языковые навыки и лучше усвоить материал. Также это дает возможность организации взаимообучения.

В конце урока учитель может собрать тетради с работами учащихся для вынесения суждения об уровне достижении цели обучения урока. Либо он может предоставить учащимся правильные ответы и организовать процесс само- или взаимооценивания.

Дополнительные задания

Уровень В

Упростите выражение .

Решение.

Уровень С

Сократите дробь .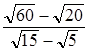

Решение.

Ответы и решения

Ответы к самостоятельной работе:

Список полезных ссылок и литературы

1.                   Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И., Феоктистов И.Е. Алгебра. 8 класс : учеб. для учащихся общеобразоват. учреждений  – М. : Мнемозина, 2010. – 384 с. : ил.

2.                   Макарычев Ю.Н., Миндюк Н.Г. Алгебра. Дидактические материалы. 8 класс: пособие для шк. с углубл. изучением математики – М. : Мнемозина, 2010. – 157 с. : ил.

3.                   Галицкий М.Л., Гольдман А.М., Звавич Л.И. Сборник задач по алгебре, 8-9 классы.  – М.: Просвещение, 2009

4.                   Феоктистов И.Е. Алгебра. 8 класс.  Дидактические материалы. Методические рекомендации. – М.: Мнемозина, 2012. – 173 с. : ил.

Скачано с www.znanio.ru