Технологическая карта темы "Комбинаторика"

Цель:

Ввести основные понятия комбинаторики,  научить решать задачи на подсчет перестановок, сочетаний и размещений.

Планируемые результаты:

Оперировать  основными  понятиями комбинаторики.  Уметь решать комбинаторные задачи. Применять полученные знания при решении  практических задач.

Основное содержание темы, термины и понятия:

Основные     понятия   комбинаторики.     Задачи   на   подсчет    числа размещений, перестановок, сочетаний. Решение задач на перебор вариантов.  Формула    бинома    Ньютона.   Свойства    биноминальных     коэффициентов.  Треугольник Паскаля.

Темы уроков

Основные понятия комбинаторики.

Правила комбинаторики

Решение задач на подсчёт числа размещений, перестановок, сочетаний.

Практическая работа №24 Нахождение числа размещений, перестановок

Практическа

я работа

№25

Решение задач на  перебор вариантов

Формула бинома Ньютона. Свойства биноминальных  коэффициентов Практическая работа №26 Нахождение биномиальных коэффициентов

Треугольник Паскаля. Практическая работа №27 Разложение многочлена п-ой степени

Решение  прикладных  задач.

Практическа я работа №28 Решение  комбинаторн ых задач

Количество часов

2

1

2

1

1

2

2

3

Основные виды учебной деятельности

Изучить  правила  комбинаторики  и  уметь применять их при  решении  комбинаторных задач.

Решать     комбинаторные       задачи   методом     перебора     и    по    правилу  умножения.  Ознакомиться        с      понятиями   комбинаторики :              размещениями, сочетаниями      и    перестановками, формулами для их вычисления. Объяснять   и   применять   формулы   при  решении  задач.

Ознакомиться  с  биномом  Ньютона и треугольником Паскаля.   Решать    практические   задачи    с  использованием      понятий     и    правил  комбинаторики.

Формы контроля

Лекция с элементами беседы

Фронтальный опрос

Индивидуаль ная работа

Тестирование

Работа в группах

Индивидуальные задания

Диктант 

Самостояте льная работа

Тема

 Основные понятия комбинаторики

Цели урока

 Ввести понятия комбинаторики. Научить различать комбинаторные задачи.

Тип урока

 Урок открытия новых знаний.

Организационные формы урока

 Фронтальная, индивидуальная

№

     Этапы урока

Деятельность учителя

Деятельность ученика

Планируемые результаты

Предметные 

УУД

1

Орг. этап

   Приветствие учащихся, проверка готовности к уроку

Подготовка к уроку

Самоконтроль, готовность к уроку (Р)

2

Мотивирование  учебной деятельности

  Лекция с элементами беседы.

  Отдельные комбинаторные задачи решали в древней Индии, Китае, античной       Греции. Классическая задача комбинаторики: «сколько есть способов

извлечь m элементов из N возможных» упоминается ещё в индийских трудах ( IV века до н. э.) Тем не менее, как самостоятельная научная дисциплина комбинаторика стала выделяться из математики только в XVII-ом столетии. 

Рождение комбинаторики как раздела математики связано с трудами Б. Паскаля и П. Ферма по теории азартных игр. Большой вклад в развитие комбинаторных методов внесли Г.В. Лейбниц, Я. Бернулли и Л. Эйлер.

Комбинаторика занимается подсчетом различных комбинаций, которые можно составлять из определенных элементов конечного множества. В переводе с латинского слово означает «сочетать», «соединять». Движущей силой в развитии науки явились азартные игры. Приведите примеры игр, где разыгрываются комбинации.

Делают записи по мере изложения материала

Приводят примеры.

 Понятия комбинаторики, размещение, сочетание, перестановки

 Осознание цели урока (Р Знаковосимвольные действия

3

Актуализация и фиксирование индивидуальных затруднений

Рассмотрим основные понятия комбинаторики

 Факториалом числа называется произведение всех натуральных чисел  от 1 до n  включительно. Причем 0!=1.

Устные ответы учащихся

 Выполнение пробного учебного действия  (Р)

1!=1

2!=1∙2=2

3!=1∙2∙3=6

4!=1∙2∙3∙4=24

5!1∙2∙3∙4∙5=120

6!=1∙2∙3∙4∙5∙6=720 и т.д.

Приведем примеры задач на подсчет комбинаций     Пусть имеется n различных объектов.

Будем переставлять их всеми возможными способами (число объектов остается неизменными, меняется только их порядок). Получившиеся комбинации называются перестановками, а их число равно Pn=n!=1 2 3 ... n

1.      Сколько различных пятизначных чисел можно составить из цифр 1, 2, 3, 4, 5 при условии, что они должны состоять из различных цифр?

Решение: Имеем перестановки из 5 элементов.

2.      Сколькими способами можно собрать 6 разноцветных лоскутков в пеструю ленту?

Решение: Имеем перестановки из 6 элементов.

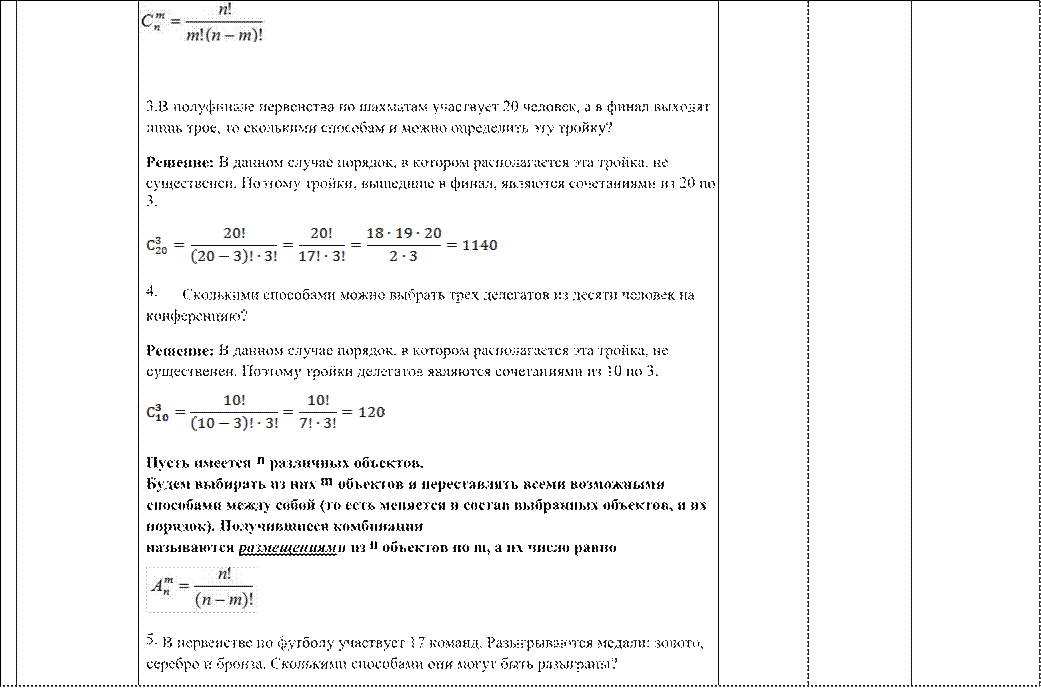
     Пусть имеется n различных объектов.

Будем выбирать из них m объектов всевозможными способами (то есть меняется состав выбранных объектов, но порядок не важен). Получившиеся комбинации называются сочетаниями из n объектов по m а их число равно 

Исправлени е ошибок.

Решение у доски и в тетрадях

  Понятия комбинаторики , размещение, сочетание, перестановки

Умение выражать свои мысли (К)

Решение: Комбинации команд-победителей отличаются друг от друга составом и порядком следования элементов, т.е. являются размещениями из 17 по 3.

6.  Научное общество состоит из 25-ти человек. Необходимо выбрать президента общества, вице-президента, ученого секретаря и казначея. Сколькими способами это можно сделать?

Решение: Комбинации руководящего состава общества отличаются друг от друга составом и порядком следования элементов, т.е. являются размещениями  из 25 по 4.

4

Выявления места и причины затруднения

   Чем отличаются рассмотренные типы комбинаторных задач друг от друга?

Ответы обучающихся

Извлечение необходимой информации (П)

5

Построение проекта выхода из затруднения

 Различать виды соединений поможет таблица.

  Заполнение таблицы:

Устные ответы учащихся Исправление ошибок.

Формулы

комбинаторик

и

Рефлексия способов и условий действий

(П)

формулы

Все ли элементы участвуют

Важен ли порядок

Перестановки

Сочетания

Размещения 

6

Первичное закрепление

  К какому виду комбинаций относится каждая задача, укажите нужную формулу для подсчета количества способов?

1.      В некоторой газете 12 страниц. Необходимо на страницах этой газеты поместить четыре фотографии. Сколькими способами можно это сделать, если ни одна страница газеты не должна содержать более одной фотографии?

2.      Сколько можно составить четырехбуквенных «слов» из букв слова «брак»?

Устные ответы учащихся

Выбор формулы

Анализ, синтез, сравнение,

обобщение(П)

3. Необходимо выбрать в подарок 4 из 10 имеющихся различных книг. Сколькими способами можно это сделать?

7

Самостоятельная работа с самопроверкой

Вариант 1.

1.              Сколькими способами 6 человек могут сесть на 6 стульев?   А. 720; Б. 120; В. 250.

2.              Сколькими способами можно выбрать 4 марки из 10 марок? 

Ответ: А. 200; Б. 252; В. 210.

Решение самостоятель но в тетрадях

  Оценка (р)

8

 Рефлексия

 Подведение итогов