Технологическая карта "Теорема Пифагора"

Автор: Духанина Екатерина Алексеевна, учитель математики МБОУ В(С)Ш № 1 г. Новосибирск

Предмет: геометрия

Класс: 8

УМК: Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. и др.

Тема урока: теорема Пифагора

Тип урока: урок развивающего контроля

Цель: закрепление знаний по теме «теорема Пифагора», полученных на уроках геометрии

Задачи:

·         решение задач на тему «теорема Пифагора»

·         рассмотрение задач из сборников ЕГЭ на тему «теорема Пифагора»

·         обзор применения «теоремы Пифагора» в жизни

Прогнозируемые результаты

личностные:

·         формирование внимательности и навыков самоконтроля при проверке правильности решения задач

·         умение грамотно и чётко излагать свои мысли

·         формирование устойчивой мотивации к учебной и трудовой деятельности

метапредметные:

·         формирование навыка нахождения наиболее рационального решения задачи

·         формирование навыка работы в условиях ограниченного времени

предметные:

·         повторение понятий «гипотенуза», «катет»

·         знание теоремы Пифагора и основной формулы, связанной с теоремой

·         доказательство теоремы Пифагора

·         решение прикладных задач по теме «теорема Пифагора»

·         выявление пробелов в знаниях по теме «теорема Пифагора»

·         умение применять знания по теме «теорема Пифагора» при решении задач ЕГЭ

Формы обучения: индивидуальная, групповая

Оборудование урока: карточки по вариантам, Smart Board

Ход урока

I урок

1.         Мотивация

Деятельность учителя: ведёт диалог с учениками, мотивирует к познавательной деятельности, поясняет необходимость знания логарифмов в большинстве профессий

Деятельность обучающихся: диалог с учителем, ответы на вопросы

УУД: регулятивные: формирование мировоззрения относительно необходимости знания теоремы Пифагора в жизни и профессии, целеполагание, познавательные – получение знаний по предмету, коммуникативные – формирование коммуникативных компетенций во время диалога с учителем и одноклассниками

Здравствуйте, уважаемые ученики! Сегодня Вам предстоит написать самостоятельную работу на тему «теорема Пифагора».

А знаете ли Вы, где в жизни применяются теорема Пифагора?

1)      Нахождение минимального расстояния между двумя точками и определения кратчайшего маршрута для минимального времени транспортировки груза.

2)      Роботы (в том числе и бытовые) выбирают кратчайший путь для построения маршрутов для экономии батареи.

3)      Для проектирования конструкций: мостов, эстакад, в промышленном и гражданском строительстве.  Для верного расчёта устойчивости конструкций производится расчёт равнодействующей силы, который производится на основании теоремы Пифагора

4)      В проектировании электронный устройств (компьютерных и телефонных плат и т.п.). Для компактности конструкции с помощью теоремы Пифагора вычисляют кратчайшие пути соединения электронных компонентов

5)       В радиотехнике: для вычисления оптимальной высоты и положения антенны путем расчёта расстояния от приёмника с целью максимизации зоны сигнала

Как Вы видите, теорема Пифагора применима в каждой профессии и в быту!

2.       Актуализация

Деятельность учителя: организует опрос о том, что вызвало сложность при освоении темы

Деятельность обучающихся: диалог с учителем, ответы на вопросы опроса по выявлению сложностей при освоении темы перед самостоятельной работой, решение заданий на повторение, обсуждение заданий и решений с одноклассниками.

УУД: регулятивные – оценка уровня подготовки обучающихся и выявление сложность при освоении темы, закрепление знаний, познавательные – структурирование знаний по теме урока, личностные - формирование внимательности, усидчивости.

На прошлом уроке проводилось тестирование для выявления психологических барьеров и страхов учащихся, возникающих перед самостоятельными работами, тестами и экзаменами.

1)        Что вызвало наибольшую сложность при освоении материала?

а) нехватка количества рассмотренных примеров и задач

б) трудности с запоминанием формул

в) нехватка практических примеров применения темы в жизни

г) недостаток иллюстративного материала

д) недостаток времени на подготовку к самостоятельной работе

2)        Сколько времени вы отводите для подготовки к самостоятельной работе? (развёрнутый ответ)

3)        В какой форме Вам больше нравится урок развивающего контроля?

а) в форме задач с развёрнутым решением

б) в форме тестов

в) в форме устного ответа на вопросы

г) свой вариант

По результатом теста подавляющее большинство обучающихся (37% и 28%) испытывают сложности, связанные с недостатком времени на подготовку к самостоятельной работе и запоминанием формул. Уважаемые ученики! Давайте повторим основные моменты по теме урока! Как называются стороны прямоугольного треугольника?

Правильно! Катет и гипотенуза (слайд 14)

А помните ли Вы основную формулу теоремы Пифагора?

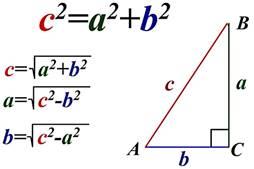
(В любом прямоугольном треугольнике сумма квадратов длин двух катетов равна квадрату длины гипотенузы)

А помните ли Вы доказательство данной теоремы?

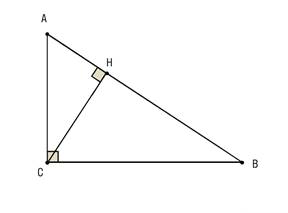Докажем, что в прямоугольном треугольнике сумма квадратов длин двух катетов равна квадрату длины гипотенузы, т.е.

AC²+CB²=AB²

Проведем высоту СН к гипотенузе ∆АВС – АВ.

При этом ∆АHC~∆ABC по двум углам: ∠HAC=∠CAB (общий), ∠AHC=∠ACB=90^o.

Тогда для данных треугольников

==> АС²=AH∙AB;

Аналогично для ∆BHC~∆ABC по двум углам: ∠HBC=∠CBA (общий), ∠CHB=∠ACB=90^o.

Тогда для данных треугольников

==> CB²=HBAB;

Таким образом, АС²+ CB²= AH∙AB+ BH∙AB=AB∙(AH+HB)= AB∙AB= AB²

Предлагаю перед самостоятельной работой потренироваться на простых заданиях.

На интерактивной доске представлено 5 треугольников. Вам необходимо соотнести треугольник и его  искомую сторону.

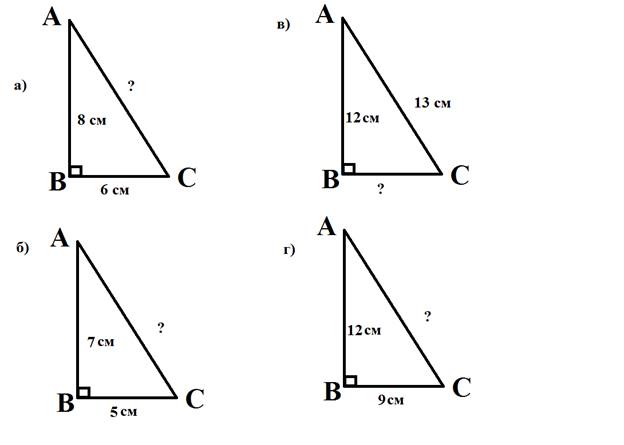
1)      15

2)      10

3)      √74

4)      5

Обменяйтесь решениями с соседом по парте. Проверьте решение соседа по парте в соответствии с решением, приведённым на слайде. Обсудите ошибки, прокомментируйте верное решение. Какое задание показалось Вам самым трудным?

Верное решение:

а) AC=====10 (2)

б) AC==== (3)

в) BC====5 (4)

г) AC=====15 (1)

Поскольку много ребят боится забыть формулы, я, основываюсь на опыт коллег из вузов, предлагаю один раз в течение 1 минуты воспользоваться письменными конспектами. Перед занятием собираются подписанные тетради с конспектами и выдаются по просьбе ученика. Выполняйте задания вдумчиво, внимательно читайте условие. Желаю удачи!

3.       Решение индивидуальных заданий по вариантам.

Деятельность учителя: организует проведение самостоятельной работы, контролирует обучающихся, отвечает на организационные вопросы.

Деятельность обучающихся: написание самостоятельной работы.

УУД: Познавательные – формирование компетенций по выбору эффективного решения задач,  личностные – формирование стрессоустойчивости, навыков работы в условиях ограниченного времени, концентрации внимания, регулятивные – прогнозирование уровня освоения знаний.

Самостоятельная работа (на решение заданий отводится 25 минут):

1)      Наибольшая из диагоналей ромба равна 48см, а сторона ромба равна 25см. Найдите наименьшую диагональ ромба. 

2)      Мама, работающая учителем в той же школе, где учится её сын, пошла с работы домой через продуктовый магазин (см. схему). Расстояние до продуктового магазина 300 м, а от магазина до дома 400м. Известно, что дороги от школы до магазина и от магазина до дома перпендикулярны друг другу. Сын пошел после учёбы домой по кратчайшему пути. На сколько метров больше прошла мама, чем сын?

3)      В прямоугольной трапеции основания равны 8см и 20см, а большая боковая сторона 20 см. Найдите периметр трапеции.

4)      Является ли прямоугольным треугольник со сторонами 2см, 3см, 8см?

5)      *Прямоугольный треугольник с меньшим катетом 3 см вписан в окружность радиусом 2 см. Найти площадь треугольника.

* Дополнительное задание повышенной сложности

II урок

4. Самоконтроль и самооценка

Деятельность учителя: объясняет верное решение задач самостоятельной работы, отвечает на вопросы, анализирует затруднения обучающихся.

Деятельность обучающихся: сверяют решения с эталоном, ведут диалог с учителем и одноклассниками, разработка и решение задач, аналогичных заданиям из самостоятельной работы/задач повышенной сложности.

УУД: регулятивные – выявление пробелов в знаниях, анализ проделанной работы, личностные - формирование картины о своих знаниях и умениях.

Здравствуйте! На прошлом занятии проводилась контрольная работа на тему «теорема Пифагора». Сейчас я оглашу результаты.

Каждому ученику раздаются проверенные работы. На слайде – правильные ответы.

1)      Наибольшая из диагоналей ромба равна 48см, а сторона ромба равна 25см. Найдите наименьшую диагональ ромба. 

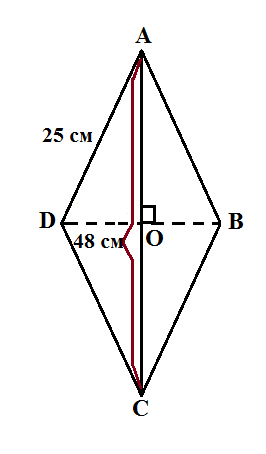
Изобразим ромб, описанный в тексте задачи.

По рисунку диагональ ромба АС=48 см, сторона АD=25 см=AB=AC=CD

Согласно свойству 1 диагоналей ромба диагонали ромба, пересекаются и точкой пересечения делятся пополам.

Соответственно, АО=ОС=48 см/2=24 см

Согласно свойству 2 диагоналей ромба диагонали ромба взаимно перпендикулярны.

Соответственно, ∆ADC – прямоугольный, в котором АD-гипотенуза, а AO и ОD – катеты. При этом согласно свойству 1 диагоналей ромба ОD – половина наименьшей диагонали ромба.

Найдем ОD по теореме Пифагора:

ОD=====7 см

Отсюда следует, что DB=2∙OD=2∙7 см=14 см

2)      Мама, работающая учителем в той же школе, где учится её сын, пошла с работы домой через продуктовый магазин (см. схему). Расстояние до продуктового магазина 300 м, а от магазина до дома 400м. Известно, что дороги от школы до магазина и от магазина до дома перпендикулярны друг другу. Сын пошел после учёбы домой по кратчайшему пути. На сколько метров больше прошла мама, чем сын?

Пути мамы и сына представляют собой прямоугольный треугольник со сторонами:

·         Путь от школы до магазина (меньший катет) – 300м,

·         Путь от магазина до дома (больший катет) – 400 м,

·         Путь прямиком от школы до дома (гипотенуза) – неизвестен

            Соответственно, путь от школы до дома (пройденный сыном) можно вычислить по теореме Пифагора. Он составит ===500 (м)

            Таким образом, мама прошла 300+400=700 м,

            Это больше на 700-500=200 м, чем прошёл её сын.

3)      В прямоугольной трапеции основания равны 8см и 20см, а большая боковая сторона 20 см. Найдите периметр трапеции.

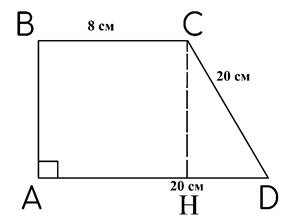
 Изобразим трапецию, описанную в тексте задачи.

В трапеции ВС=8 см, AD=20 см, CD=20 см

Если провести высоту CН, то CН=АВ, т.к. АВСН – прямоугольник (поскольку ∠ВАН=∠АВС=90^о в прямоугольной трапеции, а ∠АНС=90^о, поскольку CН – высота, то и четвертый угол ∠ВСH=90^о, т.к. сумма углов четырехугольника 360^о)

Также в прямоугольнике АВСН ВС=АH=8 см. Соответственно, HD=AD-AH=20-8=12 (см)

Тогда по теореме Пифагора в ∆СDH CH=====16 (см)

В прямоугольнике АВСН АВ=СH=16 см.

Тогда периметр трапеции ABCD составит АВ+ВС+CD+DA=16+8+20+20=64 см

4)      Является ли прямоугольным треугольник со сторонами 2см, 3см, 8см?

Предполагаемой гипотенузой является наибольшая сторона – 8 см. Соответственно, предполагаемые катеты – 2 см и 3 см.

По теореме Пифагора должно выполняться равенство  =8 (см)

Но ==≠8 (см)

Таким образом, треугольник со сторонами 2см, 3см, 8см не является прямоугольным.

5)      *Прямоугольный треугольник с меньшим катетом 3 см вписан в окружность радиусом 2 см. Найти площадь треугольника.

Изобразим треугольник и окружность, описанные в тексте задачи.

В ∆АВС АС=3 см, ОС= 2 см, где О – центр окружности.

Согласно теореме центр окружности, описанной вокруг прямоугольного треугольника, лежит на середине гипотенузы, а радиус этой окружности равен половине гипотенузы.

Соответственно, BO=OC= 2 см,

Тогда ВС=ВО+ОС=2+2=4 (см)

По теореме Пифагора АВ====

Таким образом, площадь прямоугольного треугольника составит S_ABC=∙АВ∙АС=∙∙3=

Ребята! Внимательно просмотрите задания, в которых Вы допустили ошибки!

Пожалуйста,  выпишите темы, в которых Вы допустили ошибки. Что чём конкретно было сделано неверно? Например: неверно понята суть задания; ошибка по невнимательности при переписывании условия; расчетная ошибка; ошибка в записи свойства, на основании которого производилось решение и т.д. Если ошибки не были допущены, предлагаются индивидуальные карточки с заданиями повышенного уровня сложности (приложение 1).

Перепишите решение задач, в которых Вы допустили ошибки.

Повторите тему, в которой допущена ошибка. Придумайте и решите по 5 заданий на каждую тему, в которой была допущена ошибка. Обменяйтесь решением с соседом, проверьте решения друг у друга. Повторились ли ошибки на этом этапе?

5. Рефлексия

Деятельность учителя: ведёт диалог с учениками, подводит итоги урока, выслушивает предложения учеников по улучшению качества проведения урока.

Деятельность обучающихся: подведение итогов урока, оценка урока.

УУД: Познавательные – умение объективно оценивать свою работу на уроке и деятельность учителя, личностные – умение делать выводы и вносить предложения по увеличению эффективности на уроке.

Давайте подведем итоги урока. Понравился ли Вам урок? Как Вы оцениваете свою работу на уроке?

Домашнее задание:

1)      Найдите периметр прямоугольного треугольника, если его гипотенуза равна 13 см, а меньший катет – 5 см.

2)      Лестницу длиной 5 м прислонили к дереву. На какой высоте (в метрах) находится верхний ее конец, если нижний конец отстоит от ствола дерева на 4 м?

3)      Сторона равностороннего треугольника равна 16 см. Найти площадь треугольника

4)      В прямоугольнике одна сторона равна 30, а диагональ равна 50. Найдите площадь прямоугольника.