
Технологическая карта урока
Предмет: алгебра
Класс: 8 класс
Учитель: Емельянова М.С.
Тема урока: _Решение систем неравенств с одной переменной
Учебник: Макарычев Ю. Н, Миндюк Н. Г., Нешков К. И., Суворова С. Б.; Под ред. С. А. Теляковского, Алгебра: Учеб. для 8 кл. общеобразоват. учреждений /-М.:Просвещение,2019.
Тип урока: урок закрепления знаний.
Цель: повторить решение линейных неравенств; решения систем линейных неравенств; закрепить умение решать системы линейных неравенств любой сложности.
Планируемые образовательные результаты
|
Личностные |
Метапредметные |
Предметные |
|
Умение аргументировать свою точку зрения, общаться в коллективе, слушать собеседника и вести диалог. Развивать активность и находчивость при решении задач,. |
Увидеть роль и место математики в других дисциплинах и окружающей жизни; уметь обрабатывать информацию; выбирать способы решения неравенств в зависимости от конкретных условий; контролировать и оценивать процесс и результаты своей деятельности |
уметь решать линейные неравенства и системы; графически изображать множество их решений, а также записывать решения в виде числового промежутка; производить отбор решений по заданному условию (целые решения, наибольшее/наименьшее целое решение). |
Задачи:
- образовательные (формирование познавательных УУД): Расширить, обобщить и систематизировать знания о линейных неравенствах и системах линейных неравенств; сформировать умение:
решать системы линейных неравенств, графически изображать множество их решений;
находить все целые числа, являющиеся решением системы неравенств;
находить наибольшее/наименьшее целое решение системы неравенств;
наблюдать, анализировать, делать выводы, осмысливать и обобщать учебный материал;
закреплять и повторять ранее пройденный материал.
- воспитательные (формирование коммуникативных и личностных УУД):
умение слушать и вступать в диалог, участвовать в коллективном обсуждении проблем, интегрироваться в группу сверстников и строить продуктивное взаимодействие, воспитывать ответственность и аккуратность.
- развивающие (формирование регулятивных УУД)
развивать умение анализировать, сравнивать, обобщать, делать выводы, развивать внимание, математическую речь, формировать коммуникативную компетенцию учащихся; выбирать способы решения задач в зависимости от конкретных условий; рефлексия способов и условий действия, контроль и оценка процесса и результатов деятельности.
Формы работы учащихся: Фронтальная, индивидуальная, групповая.
Оборудование и программное обеспечение: презентация к уроку , карточки, учебник.
Используемые технологии: проблемные ситуации, информационные, технологии критического мышления ( «Верю- не верю», «Дерево знаний», «З-Х-У», работа в парах, рефлексия.
|
№ |
Этап |
УУД |
Деятельность |
ИКТ, наглядность |
Время |
|
|
Учителя |
Обучающегося |
|||||
|
1. |
Организационный |
Регулятивные УУД Структурирование знаний; Прогнозирование; Формулирование проблемы; Целеполагание;
Коммуникативные УУД: Умение выражать свои мысли;
Личностные УУД: Умение выделять нравственный аспект поведения Познавательные УУД: Поиск и выделение информации; Смысловое чтение; Построение логической цепи рассуждений; Структурирование знаний; Выдвижение гипотез и их обоснование Коммуникативные УУД: Учебное сотрудничество; Регулятивные УУД Коррекция-внесение необходимых дополнений и корректив.
Регулятивные УУД Оценка-выделение и осознание учащимся того, что уже усвоено и что еще подлежит усвоению, осознание качества и уровня усвоения.
Познавательные УУД: Поиск и выделение необходимой информации. Структурирование знаний. Построение логической цепи рассуждений. Осознанное и произвольное построение речевого высказывания в устной форме;
Регулятивные УУД
Оценка-выделение и осознание учащимся того, что уже усвоено и что еще подлежит усвоению, осознание качества и уровня усвоения.
Планирование, прогнозирование
Личностные УУД: Развитие познавательных интересов.
Регулятивные УУД Планирование своей деятельности в паре для решения поставленной задачи.
Коммуникативные УУД: Поддержание здорового духа соперничества для поддержания мотивации учебной деятельности; планирование учебного сотрудничества со сверстниками; участие в обсуждении
Регулятивные УУД Планирование своей деятельности в паре для решения поставленной задачи.
Коммуникативные УУД: Планирование учебного сотрудничества со сверстниками; участие в обсуждении
Личностные : развитие критического (креативного) мышления, умения логического построения выводов, гипотез, умение находить и доказывать ошибки.
Коммуникативные: умение с достаточной полнотой и точностью выражать свои мысли; Познавательные: рефлексия.
Д/з включает в себя как репродуктивное задание, так и творческое, что позволяет вызвать у детей познавательный интерес. Формируются познавательные УУД
|
Приветствую учащихся, организую начало урока. Наш урок я хочу начать с высказывания Рене Декарта « Математика учит преодолевать трудности и исправлять собственные ошибки» Ребята над какой темой урока мы с вами Работаем? Откройте ваши тетради запишите число и тему урока. |
Приветствуют учителя, настраиваются на урок
Формулируют тему урока.
|
|
2 мин.
|
|
2.
3
4
5
6
7
8
|
Мотивация и актуализация знаний
Проверка домашнего задания
Применение знаний
Решение проблемного вопроса Восприятие и осмысление учащимися нового материала. Проверка пониманий.
Физминутка
Закрепление знаний.
Решение задач из ОГЭ
9. Рефлексия (подведение итогов урока)
10.Информация о домашнем задании, инструктаж по его выполнению.
|
Для повторения теории темы, ее понимания и умения применять проведем небольшую разминку . Ребята, посмотрите на доске у нас «Дерево знаний». Сейчас по желанию кто-нибудь один выходит к доске и отвечает на вопросы. Ребята, скажите какая цель будет нашего урока? Тестирование с последующей проверкой, работа в парах. Поиграем в «Верю - не верю». Каждое задание теста предполагает ответ «Да» или «Нет». «Да» -1 «Нет» - 0. Вопросы теста: 1)Является ли число 12 решением неравенства 2х>10? 2) Является ли число -6 решением неравенства 4х>12? 3) Является ли неравенство 5х-15>4х+14 строгим? 4) Существует ли целое число принадлежащее промежутку [-2,8;-2,6]? 5) При любом ли значении переменной а верно неравенство а² +4 >о? 6) Верно ли, что при умножении или делении обеих частей неравенства на отрицательное число знак неравенства не меняется?
Кто смог решить дома № 883? Такие задания встречаются на ОГЭ. Постановка проблемы: что такое допустимые значения переменной и как решать задачи на нахождение допустимых значений переменной? Давайте вместе проанализируем и применим наш прием «З - Х- У» («З»- знаем, «Х- хотим узнать, «У»-узнали - Что мы знаем? Устные дополнительные вопросы 1.Сформулируйте основные свойства неравенств, используемые при решении и доказательстве неравенств и их систем? 2.Что называется решением системы неравенств? 3.Алгоритм решения системы неравенств? (Уточнить алгоритм)
- Что мы хотим узнать?
- Ну а на вопрос «Что узнали?» ответим позднее. Применим наши знания для решения задач.
Вернемся к № 883(в,г). Кто пойдет к доске? –
Сколько ограничений надо учесть?
Несколько упражнений для отдыха и разминки перед следующей работой
Числовой луч – встают мальчики Открытый числовой луч – встают девочки Интервал – руки вверх Полуинтервал – хлопаем в ладоши
На доске даны системы и несколько вариантов ответа, нужно выполнить соответствие. Установите соответствие между аналитической моделью и числовым промежутком.
Дана система неравенств, нужно найти ошибку.
Работа с заданиями из ОГЭ по данной теме на применение полученных знаний (работа в парах) Тест 1. Какой промежуток соответствует неравенству
2. Какое неравенство соответствует данному числовому промежутку?
А: 3. Решите неравенство и укажите, на каком рисунке изображено множество его решений: 3х+4
4. Какой промежуток соответствует системе неравенств?
5. Какая система неравенств соответствует данному числовому промежутку?
6. Известно, что х
7. На каком рисунке изображено множество решений х
8. Какое наименьшее целое число является решением данной системы?
А: -6; 9. Какой промежуток является решением данной системы неравенств?
А: 10. Какова область определения функции у = А: (2;
Ребята, давайте вернемся к началу нашего урока и вспомним тему, цель и проблему, которые мы обозначали. Удалось ли нам реализовать цель урока? Сегодня мы повторили, обобщили умения, знания и навыки по темам: «Решение неравенств и систем неравенств с одной переменной». Многие справились с решением неравенств и систем неравенств. Хорошо поработали на уроке. Рефлексия У каждого из вас на столе карточки. Прикрепите на доску одну карточку, уходя с урока. Был ли, на ваш взгляд, наш урок уроком обобщения, контроля и систематизации знаний? Что именно вы повторили на уроке? С каким настроением уходите? Спасибо за работу на уроке. Всего доброго!
Сегодня мы говорили о решении систем неравенств с одной переменной. № 885(а,б) – 884(а). Спасибо всем за урок!
|
Слушают учителя.
Ученики по желанию выходят к доске и отвечают на вопросы по теме урока.
Учащиеся устно выполняют предложенные задания, записывают ответы в виде 1 и 0.
Самопроверка
Фронтальная работа
Ответы учащихся: 1.Мы знаем как решать неравенства 2.Как решить систему неравенств. 3.Как записать промежутки, которые являются решением неравенства или системы
- Как находить допустимые значения выражения?
Решают задачу, анализируют, высказывают свое мнение, делают вывод Вступают в диалог, составляют неравенства
Делают упражнения анализируют, высказывают свое мнение
Делают разминку, на закрепления пройденного материала
Двое учеников выходят к доске и выполняют задание.
Работают в парах, анализируют, высказывают свое мнение, делают вывод
Работают в парах, анализируют, высказывают свое мнение, делают вывод
Отвечают на вопросы
Записывают домашнее задание |
На доске
Слайд
учебник
доска
слайд
Слайд
На доске
Слайд
|
5 мин.
7 мин.
7 мин
4 мин
5 мин
10 мин
3 мин
2 мин
|
|
Разрезные карточки для двух учащихся:
|
|
|
|
|
|||
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Работа с заданиями из ОГЭ по данной теме на применение полученных знаний (работа в парах)
|
1.На каком рисунке изображено множество решений системы
неравенств ![]()
![]()
2. Какая система неравенств соответствует данному числовому промежутку?
![]()
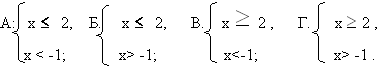
3.
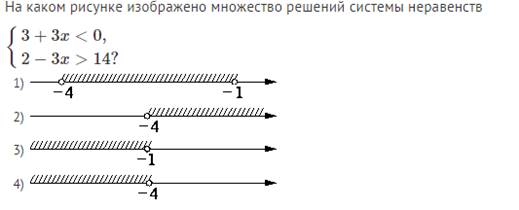
4. Укажите допустимые значения переменной у =![]()
А: (2;![]() );
Б: (-
);
Б: (-![]() ;
2]; В: [2;
;
2]; В: [2;![]() );
Г: (-
);
Г: (-![]() ;2).
;2).
При решении числовых неравенств можно:
1) переносить слагаемые из одной части неравенства в другую, изменив знаки этих слагаемых на противоположные;
2) делить обе части неравенства на одно и то же положительное число, сохраняя знак неравенства;
3) ) делить обе части неравенства на одно и то же положительное число, сохраняя знак неравенства
Решить неравенство:
-2(х – 3) > 3(x + 5).
Решение:
Раскроем скобки, умножив числа перед скобками на каждое слагаемое в скобках: -2х + 6 > 3x + 15.
Перенесём слагаемые с неизвестным влево, а без неизвестных вправо, изменяя их знаки: -2х – 3х > 15 – 6.
Приведём подобные слагаемые:
-5х > 9, разделим обе части неравенства на отрицательное число – 5, меняя знак неравенства: х< -1,8.
Ответ: ![]()
1) х - 4 > 8;
2) 5 + x < 9 ;
Решение систем неравенств 1 степени
Образец решения системы неравенств![]()
|
1)Решим 1неравенство:
|
2) Решим 2 неравенство:
|
3) Нанесём решения 1 и 2 неравенств на одну числовую прямую:

![]() 3
3
Ответ: ![]() или
или ![]()
а) Реши самостоятельно:
![]()
|
1)Решим 1 неравенство
|
2)Решим 2 неравенство
|
Нанесём решения 1 и 2 неравенств на одну числовую прямую:
![]()
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.