ТОЧНЫЕ И ПРИБЛИЖЕННЫЕ ЧИСЛА

Точные и приближенные числа

З а д а н и е  1. Для математических понятий слева найдите соответствующие справа:

равенство                  меньше

четные                       приближенные

точные                       неравенство

больше                       нечетные

З а д а н и е  2. Найдите выражения, в которых числовые значения приближенные: на лугу распустились около тысячи ромашек, в классе 7 девочек, в парке 7 дубов, в коробке 6 карандашей, в небе тысячи звезд, в книге примерно 400 страниц.

Точное количество населения города Михайловки 300 540 человек. Чему может быть равно приближенное?

Чему равна разность между точным и приближенным значением?

З а д а н и е  3. Найдите значения выражений.

Расположив ответы в порядке уменьшения значений, вы узнаете, как называется разность между точным и приближенным значением.

17 ´ 6     19 ´ 24      32 ´ 46      127 ´ 8      267 ´ 123      3164 : 4 29519 : 7     680 : 4      29349 : 9      7005 ´ 34      2215 : 5

1472 – е    791 – н      3261 – р      102 – ь    456 – о     32841 – о 1016 – ш     4217 – г     238170 – п      170 – т      443 – с

О т в е т: погрешность.

З а д а н и е  4. Назовите приближенные значения:

1) если масса арбуза 3 кг 200 г, 5 кг 890 г,

2) длина отрезка 5см 3 мм, 5 см 7 мм,

3) расстояние от города до села 7 км 160 м, 8 км 960 м,

4) стоимость книги 6 р.10 к., 6 р. 97 к.

З а д а н и е  5. Найдите выражения, для которых значения являются погрешностью.

Рассматривая выражения по горизонтали и выписывая буквы, соответствующие им, ты узнаешь, насколько правильно выполнил задание.

13 ´ 4 = 52 (б)            256 + 44 = 300 (к)           5640 – 5600 = 40 (в)

5640 – 5000 = 640 (е)

160 : 4 = 40 (с)           310 – 300 = 10 (р)         5640 – 640 = 5000 (у)

7320 – 7300 = 20 (н)

5640 – 40 = 5600 (ж)       310 – 10 = 300 (л)         300 – 44 = 256 (ф)

7320 – 7000 = 320 (о)

О т в е т: в результате получается слово-подсказка «верно».

З а д а н и е  6. Замените точные числа приближенными, найдите разные решения: 1547, 12 346, 154 927, 309 406, 370 241.

З а д а н и е  7. Разделите значения на две группы:

а) с избытком;                   б) с недостатком

З а д а н и е  8. Округлите:

1) В городе 42 376 человек, округлите это число до сотен человек.

2) Взвесили сахарный песок, насыпанный в чайный стакан, при этом вес его оказался равный 247 г. Округлите это число до десятков граммов.

3) Измерили рулеткой длину и ширину школьного двора и получили следующие данные: длина 57 м 8 дм, ширина 32 м 2 дм. Округлите эти числа до целых метров. Найдите площадь, округлите до целых кв. м.

О т в е т: площадь равна 186 116 кв. дм., это примерно 1 861 кв. м.

Логические задачи.

Решение задач при помощи схем, чертежей и рисунков

1. Расставь скобки так, чтобы получились верные равенства.

211 – 126 – 74 х 8 = 88

12 х 16 + 128 : 8 + 24 = 240

12 х 1 6+ 128 : 8 + 24 = 196

2. Сумма двух чисел равна 462. Одно из них оканчивается нулем. Если этот нуль зачеркнуть, то получится второе число. Найдите это число. (420 и 42.)

3. По углам и сторонам квадрата вбиты колышки на расстоянии 2 м друг от друга. Сколько колышек вбито, если сторона квадрата равна 10 м? (20 колышков.)

4. Часы бьют каждый час и отбивают столько ударов, сколько показывает часовая стрелка. Сколько ударов отбивают часы в течение 12 часов?

5. В углах квадратной клумбы растут кусты – всего 4 куста. Площадь клумбы увеличили в 2 раза, не выкапывая кустов. Расширенная клумба тоже квадратная, а внутри нее кустов нет. Как это сделали? Выполните чертеж.

6. Иванов, Петров, Сидоров и Козлов по математике за контрольную работу получили четыре оценки: 2, 3, 4, 5. Известно, что Петров списал у Сидорова, но сделал это невнимательно. Иванов не справился ни с одним из заданий. Лучше всех решил Козлов. Какую оценку получил каждый ученик?

7. Как набрать из водопровода 6 литров воды, пользуясь двухлитровой банкой и чайником, в который входит 5 л?

8. В семье четверо детей: им 5, 8, 13, 15 лет. Зовут их Таня, Юра, Света и Лена. Сколько каждому из них, если одна из девочек ходит в детский сад, Таня старше, чем Юра, а сумма лет Тани и Светы делится на 3? (Света – 5 лет; Юра – 8 лет; Татя – 13 лет; Лена – 15 лет.)

9. Шпунтик и его друзья из данных фигур составляли новые. Каждый из них из двух таких многоугольников, как показано на рисунке, составил новый и нашел сумму длин его сторон. Ответы у них получились разные, но у всех правильные. Как такое могло быть, и какие ответы у них получились?

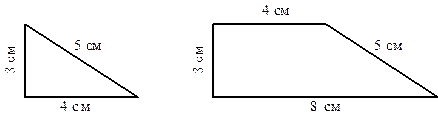
10. На складе находилось 7 полных бочонков меда, 7 наполовину наполненных медом и 7 пустых. Как распределить все бочонки между тремя покупателями так, чтобы каждый получил одинаковое количество бочонков и меда. Найдите решение, при котором мед не нужно перекладывать из одного бочонка в другой.

О т в е т: дать каждому по 2 полных, затем первому и второму по 2 наполовину наполненных и по 2 пустых; затем третьему 1 полный и 3 пустых, потом каждому по одному наполовину наполненных.

Проверочный тест

1. Восстановить записи:

2. Соединить числа 1280, 740, 600, 60 математическими знаками «плюс» и «минус» так, чтобы в результате получился ноль (не применяя скобок)

3. У Алеши 4 кубика разного цвета: синий, красный, желтый, зеленый. Сколькими способами он может построить пирамиду из трех кубиков?

4. Задумали число. Если к нему прибавить наибольшее трехзначное число, а затем разделить на 10, то получится наименьшее трехзначное число. Какое число задумали?

5. Молоком наполнили доверху 4 одинаковых стакана. Во всех стаканах столько молока, сколько в банке. В стакане и в банке вместе 1 кг 200 г молока. Сколько граммов молока в стакане?

О т в е т: в стакане 240 г; в банке 960 г.

6. Отнимите 4 палочки так, чтобы образовалось 5 одинаковых и 5 различных по величине квадратов. Покажите два способа решения.

7. Три брата поймали 29 карасей. Когда один брат отловил для ухи 6 штук, второй – 2, а третий – 3, то у каждого брата осталось равное количество рыб. Сколько карасей поймал каждый брат?

Р е ш е н и е:

1) 6 + 2 + 3 = 11 (карасей) – взяли для ухи.

2) (29 – 11) : 3 = 6 (карасей) – осталось у каждого.

3) 6 + 6 = 12 (карасей) – было у первого.

4) 2 + 6 = 8 (карасей) – было у второго.

5) 3 + 6 = 9 (карасей) – было у третьего.

О т в е т: 12, 8 и 9 карасей.

8. Задачи профессора Пятеркина.

а) Профессор Пятеркин жил в квартире № 13. Большой любитель математики, профессор решил номер своей квартиры записать необычным образом – с помощью пяти троек. Какие знаки арифметических действий он должен был поставить между некоторыми тройками, чтобы получить 13? (3  3  3  3  3 = 13)

б) Когда профессор Пятеркин переехал в новую квартиру № 31, он решил номер своей новой квартиры тоже записать необычным образом – с помощью пяти пятерок. Поставьте знаки арифметических действий между пятерками и получите 31.    (5  5  5  5  5 = 31)

О т в е т: а) 3 × 3 + 3 + 3 : 3 = 13;   б) 5 × 5 + 5 + 5 : 5 = 31.