Треугольники

Конспект открытого урока по геометрии по теме

«Треугольники»

 

Класс: 7

 

Учитель: Ильина Ирина Васильевна

 

Тема:  Итоговое повторение темы «Треугольники»

 

Необходимое оборудование: чертежные инструменты, проекты, печатный текст.

 

Цели и задачи урока:

Образовательные:

·         повторить и систематизировать с обучающимися изученный материал по геометрии за курс 7 класса;

·          обогащать словарный запас геометрическими терминами;

·          закрепить определения и теоремы;

Развивающие:

·          развивать умение анализировать и отбирать нужную информацию;

·          развивать умения оформлять записи,  вести беседу;

Воспитательные:

·          формировать опыт ответственного выбора и ответственной деятельности: самоорганизации и самореализации;

·          формировать ситуативные информационно-коммуникативные умения: умение слушать других, уважать мнение другого человека, понимать ценностное значение предлагаемой тематической информации.

 

 

Авторский замысел: Ребятам раздаётся задание по оформлению ярких, красочных стендов-экспонатов по темам: «Определение треугольника», «Виды треугольников», «Древо треугольников», «Фигуры из треугольников», «Неравенство треугольников», «Элементы треугольников», «Признаки равенства прямоугольных треугольников». Кроме того, каждому участнику было дано задание составить свой рассказ о треугольниках по одному из стендов. После изготовления стендов оформляется кабинет под музей. Подготавливаются экскурсоводы по материалам каждого экспоната.

 

 

 

Ход занятия:

 

I. Организационным момент. (1 мин)

Здравствуйте ребята! Садитесь.

 

II. Мотивация к учебной деятельности (3 мин)

а) введение в тему: Я рада приветствовать Вас в нашем музее! Экскурсия посвящена такой важной фигуре, как треугольник. Для этого семиклассниками нашей школы был организован «Музей Треугольника».

b) Постановка цели и задач урока: Сегодня на уроке мы повторим и систематизируем изученный материал по геометрии за курс 7 класса по теме «Треугольники».

 

III. Экскурсия по музею. (30 мин)

«Определение треугольника»

(Экспонат № 1. На доске демонстрируется, почему три точки не лежат на одной прямой и как получается треугольник).

 

 

 

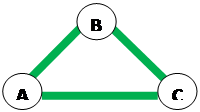
 «Мы рады приветствовать Вас в нашем музее! Экскурсия посвящена такой важной фигуре, как треугольник. Итак: Треугольником называется геометрическая фигура, состоящая из 3 точек, не лежащих на одной прямой, и трёх отрезков, соединяющих эти точки».

 «Точки называются вершинами, а отрезки сторонами. На нашем экспонате вершинами являются точки А, В, С, а сторонами – отрезки АВ, АС, ВС. У треугольника есть три угла: <АВС, <ВАС, <ВСА. Сумма всех углов треугольника равна 180°. Периметром треугольника называется сумма длин всех сторон.

Внешним углом треугольника называется угол, смежный с внутренним.

Свойство: Внешний угол треугольника равен сумме двух внутренних углов, не смежных с ним».

«Элементы треугольника».

(Экспонат № 2.  Ученики слушают следующего экскурсовода. Экскурсовод указкой показывает на стенде).

 

  

 

 

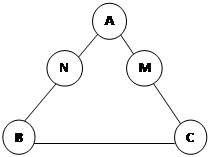
 «У треугольника есть три внутренних отрезка: медиана, высота и биссектриса.

Медианой треугольника называется отрезок, соединяющий вершину треугольника с серединой противолежащей стороны.

В каждом треугольнике есть три медианы, которые пересекаются в одной точке.

Биссектрисой треугольника называется отрезок, соединяющий вершину треугольника с противолежащей стороной и делящий угол при этой вершине пополам. Есть шуточное высказывание о биссектрисе: «Биссектриса - это крыса, которая бегает по углам и делит угол пополам

В каждом треугольнике есть три биссектрисы, которые пересекаются в одной точке.

Высотой треугольника называется перпендикуляр, проведённый из вершины треугольника к противолежащей стороне (указкой показывается на стенде). В каждом треугольнике есть три высоты, которые пересекаются в одной точке».

 «Генеалогическое древо треугольников»

(Экспонат № 3.  Ученики слушают следующего экскурсовода. Экскурсовод указкой показывает на стенде).

 «Геометрия – наука, изучающая фигуры и их свойства. В переводе с греческого «гео» – земля, «метрео» - мерить. Основными фигурами в геометрии являются точка и прямая. Из них возникли луч, отрезок, угол, а затем и треугольник. Треугольники бывают остроугольными, тупоугольными, прямоугольными, равнобедренными, равносторонними, равными. Подробнее с каждым из этих треугольников познакомимся у следующих стендов».

 «Виды треугольников»

(Экспонат № 4.  Ученики слушают следующего экскурсовода. Экскурсовод указкой показывает на стенде).

 

 

 

 

 

 

 

 

 «Остроугольным треугольником называется треугольник, у которого все углы острые.

Тупоугольным называется треугольник, у которого один угол тупой, а два других острые.

Прямоугольным треугольником называется треугольник, у которого один угол прямой, а два других острые. Подробнее о прямоугольных треугольниках мы поговорим у стенда, посвященного прямоугольным треугольникам.

Равнобедренным называется треугольник, у которого две стороны равны. Эти стороны называются боковыми, а третья – основанием. У равнобедренного треугольника имеются следующие свойства:

·                     Углы при основании равны

·                     Медиана, проведённая к основанию, является биссектрисой и высотой. Аналогичным свойством обладают и высота, и биссектриса.

Равносторонним треугольником называется треугольник, у которого все стороны равны. В равностороннем треугольнике каждый угол равен 60°. Каждая медиана является и биссектрисой и высотой, и все они пересекаются в одной точке.

В каждом их этих треугольников напротив большей стороны лежит больший угол, а напротив большего угла лежит большая сторона.

Равными называются треугольники, у которых соответствующие стороны и углы равны. Существует три признака равенства треугольников. О них подробнее мы узнаем у следующего стенда нашего музея».

 

 «Признаки равенства треугольников».

(Экспонат № 5.  Ученики слушают следующего экскурсовода. Экскурсовод указкой показывает на стенде).

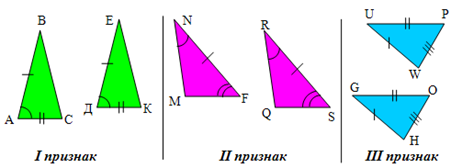
«Первый признак (его краткое название по двум сторонам и углу между ними) звучит так: если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними второго треугольника, то эти треугольники равны.

Второй признак (по стороне и двум прилегающим углам): если сторона и два прилегающих угла одного треугольника соответственно равны стороне и прилегающим углам второго треугольника, то эти треугольники равны.

Третий признак (по трём сторонам) звучит так: если три стороны одного треугольника соответственно равны трём сторонам другого треугольника, то эти треугольники равны».

 

 «Логические задачи про треугольники».

 «А теперь вашему вниманию предлагается несколько занимательных задач, связанных с треугольниками»

1)      Попробуйте составить из спичек треугольники».

Например:

·                     Из пяти спичек составить два треугольника.

·                     Из четырёх спичек составить два треугольника.

·                     Из шести спичек составить четыре треугольника.

 «Признаки равенства прямоугольных треугольников».

(Экспонат № 6.  Ученики слушают следующего экскурсовода. Экскурсовод указкой показывает на стенде).

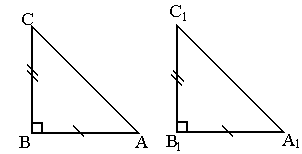
 «А теперь подробнее поговорим о прямоугольном треугольнике. В прямоугольном треугольнике две стороны, которые образуют прямой угол, называются катетами. Сторона, лежащая напротив прямого угла, называется гипотенузой. Для прямоугольного треугольника характерны следующие свойства:

·     Сумма острых углов в прямоугольном треугольнике равна 90°.

·     Гипотенуза больше каждого катета.

·     Напротив угла в 30° лежит катет, равный половине гипотенузы.

·     Если катет равен половине гипотенузы, то он лежит напротив угла 30°.

Для прямоугольных треугольников существует пять признаков их равенства всего по двум элементам. Их краткие названия следующие:

·                     по двум катетам,

·                     по гипотенузе и острому углу,

·                     по катету и прилежащему острому углу,

·                     по катету и противолежащему острому углу,

·                     по гипотенузе и катету.

 «Неравенство треугольника».

(Экспонат № 9.  Заранее к каждому объекту составлен большой треугольник, состоящий из цветных треугольников. .  Ученики слушают следующего экскурсовода. Экскурсовод указкой показывает на стенде. Ученики выполняют задания. После показа, желающие задают вопросы экскурсоводу)

 

 

 

 

 

 

 

 

 

 

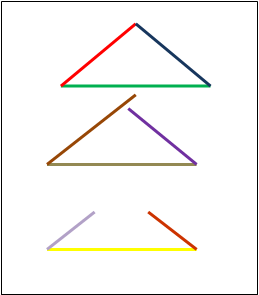«Всегда ли можно построить треугольник? Попробуйте!»

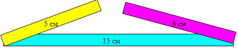
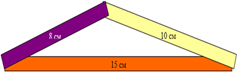
 «Итак, треугольник можно построить только в том случае, если выполняется одно важное условие: каждая сторона должна быть меньше суммы двух других сторон

«Фигуры из треугольников».

На доске заранее составлены треугольники, разрезанные на 10 маленьких треугольников следующим образом:

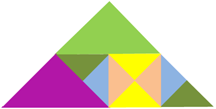
 «Посмотрите, как из треугольника, разрезанного на меньшие треугольники, можно собрать кошку, рыбку и робота»

 

 

IV.   Сценка «Треугольник и квадрат». (Ученики показывают сценку)

Автор:

Жили-были два брата
Треугольник с квадратом.
Старший – квадратный,
Добродушный, приятный.
Младший – треугольный,
Вечно недовольный.

Квадрат: Почему ты злишься брат?

Автор: Тот кричит ему:

Треугольник:

“Смотри,
Ты полней меня и шире.
У меня углов лишь три,
У тебя же их четыре!”

Автор: Но квадрат ответил:

Квадрат:

“Брат!
Я же старше, я – квадрат”.

Автор: И сказал еще нежней:

Квадрат: Неизвестно, кто нужней!”

Автор:

Но настала ночь и к брату,
Натыкаясь на столы,
Младший лезет воровато,
Срезать старшему углы.
Уходя, сказал.

 

Треугольник:

“Приятных
Я тебе желаю снов!
Спать ложился – был квадратным,
А проснешься без углов!”

Автор:

Но на утро младший брат
Страшной мести был не рад.
Поглядел он – нет Квадрата,
Онемел ... стоял без слов ...
Вот так месть! Теперь у брата ...
Восемь новеньких углов!

 

 

V. Рефлексия.

Продолжите фразы:

• Сегодня на уроке я узнал…
• Сегодня на уроке я повторил…
• Сегодня на уроке я закрепил…

 

VI. Заключение.

«Спасибо за внимание, до встречи в следующем году, ведь это не вся информация о треугольниках! Вам ещё многое предстоит узнать об этой фигуре в 8 классе».

VII. Домашнее задание.  Раздаточный материал с задачами.

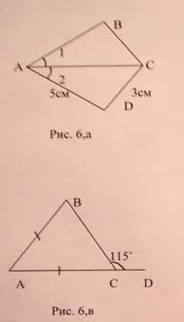
№ 1. В треугольниках АВС и ADC (рис. 6, а) 1 = 2, AD = 5cм,

        DC = 3см.                       

        Найдите AB.                                                        

        Ответы: а) 5см;             б) 3см;     

        в) недостаточно данных.                                                                 

№ 2. Периметр равнобедренного треугольника  равен 28см, а его боковая сторона равна 9см. Найдите длину основания  треугольника.       

Ответы: а) 10см;       б) 14,5см;       в) 29см.                  

№ 3. BCD =115˚ (рис.6, в). Найдите ABC.    

Ответы: а) 50˚;          б) 65˚;                         в) 75˚.