Урок-фрейм по теме «Площадь»
Обучаясь в одном классе, по одной программе и учебнику, дети могут усваивать материал на различных уровнях. Успех учебного процесса в значительной степени зависит от познавательной активности школьников, от того, насколько они заинтересованы в собственной работе.
Ясное знание конкретных целей при условии их посильности, возможность выполнять предъявляемые учителем требования активизируют познавательную деятельность учащихся, причем на разных уровнях. Если цели известны и посильны ученику, а их достижение поощряется, то для ученика нет ничего естественнее, как стремиться к их выполнению.
Открытость уровней подготовки способствует формированию положительных мотивов учения, сознательного отношения к учебе, повышению самооценки учащегося. Ученик получает возможность выбирать объем и глубину усвоения учебного материала: либо его усилия н6аправляются на овладение материалом на более высоких уровнях, либо продолжается работа по формированию важнейших опорных знаний и умений.
Данный тип урока позволяет учащимся оценить собственные силы и выбрать для себя уровень целей, соответствующий их потребностям и возможностям в данный момент, а со временем – перейти на более высокий уровень.
Фрейм (с английского рама) означает консолидацию разнородной информации, имеющей центром то или иное реальное явление, действие, событие, ситуацию, воспринятую психикой в ограниченных рамках пространства и времени.
Урок-фрейм охватывает все информационное окружение данного понятия, правила, теоремы. Примером удачного фрейма может служить шуточное представление, что позволяет ученикам вспомнить это через много лет.
Фреймовое представление знаний имеет ту особенность, что в нем поневоле участвуют как все процессоры мозга, так и наблюдения, опыты, эмоции, аналогии и гипотезы, доказанное и предполагаемое, готовое и составляемое.
Цель урока
Образовательная:
систематизировать и обобщить знания учащихся по теме «Площади»
Развивающая:
- способствовать формированию умений применять приемы: сравнения, обобщения, выделения главного, переноса знаний в новую ситуацию, анализировать условие задачи, составлять модель решения.
- способствовать развитию умений и навыков применять математические знания к решению практических задач, ориентироваться в простейших геометрических конструкциях
Воспитательная:
содействовать воспитанию интереса к математике, активности, мобильности, умения общаться.
I. Вступительное слово учителя
Урок-фрейм “Площадь” - это урок, центром которого является понятие площадь.
Фрейм (с английского рама) означает консолидацию разнородной информации, имеющей центром то или иное реальное явление, действие, событие, ситуацию, воспринятую психикой в ограниченных рамках пространства и времени.
Фрейм – рамка- знаний умений и навыков по теме «Площадь»
Фрейм охватывает все информационное окружение данного понятия, формул, теорем, свойств фигур.
Каждый знает, что учить по данной теме,
как и для чего
«рамка
знаний» по теме Площадь
3-5 класс площадь квадрата и прямоугольника
7 класс площадь треугольника
8 класс площадь трапеции, ромба, параллелограмма
10 класс площадь пирамиды, призмы
11 класс площадь тел вращения (конус, цилиндр, сфера и шар)
“Подобно тому, как рою бесчисленных пчел, поражающему наперебой своими жалами, не удается отогнать упивающегося медведя, если он хоть немного вкусил приятность скрытого в дереве меда, так нет, разумеется никого, кто, хоть краем губ постигнув сладость математических доказательств, не стремился бы всеми силами освоить их вполне, до полного насыщения”.
Реклама.
Вкусите “Площадь” - это гарантия полного насыщения”
II. Актуализация знаний
Используя таблицу основных формул:
Задание сопоставить формул с ее названием:
S= аbsinγ S= (d1×d2×sinγ) 2
Формула Геррона
S= 1/2ab sinγ S=1/2 r×P S= abc 4R
(круговой сектор) S=πR²α 360
4 n =4, S=a² n=6, S=3√3a² 2
|
(правильная пирамида) Sбок=1/2Pоснd (апофему) (усеченная пирамида) Sбок=1/2(P1 +P2)d (апофему)
Sпол=2πR(R + h)
(прямой призмы) Sбок= Ph
Sпол=πr(l + r) (усеченный конус) Sбок=π (r + r1) l
|
Реклама
Знания формул – это надежный шаг к решению многих задач. Знайте формулы.
Реклама. В3, В9 Выполнение тестов - надежный путь в сдаче ЕГЭ
Проанализировать задачи и выписать из таблицы те формулы которые будите использовать при решении задания В3 и В6:
В3: площадь квадрата , площадь прямоугольника, площадь прямоугольного треугольника
В9: площадь пирамиды, площадь призмы, площадь квадрата, площадь прямоугольника.
|
|
|
|
|
|
В9:
1. Стороны основания правильной четырехугольной пирамиды равны 10, боковые ребра равны 13. Найдите площадь поверхности этой пирамиды.
2.
В правильной треугольной пирамиде 
— середина
ребра 
, 
— вершина.
Известно, что 
, а 
. Найдите
площадь боковой поверхности.
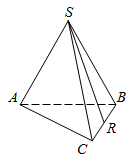
3. 
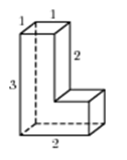Найдите площадь поверхности многогранника, изображенного на
рисунке (все двугранные углы прямые).
4. Найдите площадь поверхности многогранника, изображенного на рисунке, все двугранные углы которого прямые.
|
|
Реклама
Изучение площадей поможет Вам быстро и правильно принимать решения в различных ситуациях, так как Вы уже учитесь думать, преодолевать трудности и рассуждать, а это всё ведет к приобретению мудрости.
(ориентировать на расширение рамки, так как на следующих уроке мы рассмотрим применение темы площади для тел вращения.).
Подведение итогов. Оценивание учащихся. Вернуться к вопросу
Каждый знает, что учить по данной теме, как и для чего
расширение
границ темы «площадь»…..
Урок-фрейм по теме «Площадь»
I. Вступительное слово учителя
Используя таблицу основных формул:
В9: 1. Стороны основания правильной четырехугольной пирамиды равны 10, боковые ребра равны 13
Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые)
© ООО «Знанио»
С вами с 2009 года.
